“If I have seen further than others, it is by standing upon the shoulders of giants.” This famous quote by Isaac Newton points to an axiom that lies at the heart of The Sciences — knowledge precedes knowledge.
What we know today is entirely based upon what we learned in the past. This general pattern is echoed throughout recorded history by the revelation of one scientific mystery leading to other mysteries… other more compounding questions. In the vast majority of cases these mysteries and other questions are sprung from the source of an experiment with an unexpected outcome sparking the question: “why the hell did it do that?” This leads to more experiments which creates even more questions and next thing you know we go from moving around on horse-drawn carriages to landing drones on Mars in a few generations.
The observant of you will have noticed that I preceded a statement above with “the vast majority of cases.” Apart from particle physics, almost all scientific discovery throughout recorded history has been made via experiment and observation. There are a few, however, that have been discovered hidden within the confines of an equation, only later to be confirmed with observation. One such discovery is the Black Hole, and how it was stumbled upon on a dusty chalkboard in the early 1900s will be the focal point of today’s article.
Only A Mathematical Hypothesis
This was what Einstein had to say on the subject of Black Holes:
The essential results of this investigation is a clear understanding as to why ‘Schwarzschild singularities’ do not exist in physical reality.
He believed them to be only a “mathematical hypothesis.” It was not one of his finest papers, that’s for certain. Those of you who are learned of his views on quantum theory will not be surprised that he took such a formal vantage point. But before we get into that, let us backtrack to a point where it all began.

Einstein’s general relativity was a giant leap forward in our understanding of gravity. Newton’s theory worked, but it was unable to explain how the force originated and it failed under a handful of observable events — such as the perihelion orbit of Mercury. Einstein realized that gravity had the peculiar property of disappearing under its own effect. After looking at free-fall very carefully, he was able to explain the origin of gravity by giving space geometric properties. The presence of mass changes the geometric properties of the space around it. We sense this change as gravity.
General relativity explained mercury’s odd orbit and was all but confirmed during a 1919 solar eclipse when the bending of starlight (as it passed the curved space around the sun) was measured by an amount precisely predicted by the theory. Einstein and his theory shot to stardom, but it would not last long. For in the summer of 1916, a physicists managed to use general relativity’s intimidating field equations to calculate the curved space around a star to an exact solution. And what he found hidden deep within the complex math would send the whole of the theory crashing in on itself. This man’s name was Karl Schwarzschild.
The Schwarzschild Singularity
General Relativity was still hot off the press when Karl Schwarzschild was able to use it to find a solution that would calculate the space-time curvature around a single stationary point. The small amounts of angular momentum possessed by planets and stars would not hinder his equation’s ability to be applied to them. The Swartzschild Metric was used to calculate the sun’s space-time curvature and was confirmed during the 1919 solar eclipse. While the mathematics of the equation are complicated and well beyond the scope of this article, we can still use it to understand some basic properties of space-time around a massive object. Or more importantly, to see what happens to them under certain ‘extreme’ conditions.
The two variables we’re to be concerned with are “r” and “rs”.
- r = coordinate of a sphere around a massive point.
- rs = scalar factor of r with respect to the point’s mass, and is equal to 2GM/c2
The variable rs is also known as the Schwarzschild Radius, and is quite interesting when you apply some pressure to it. We have two things going on here: mass and radius.
If you keep cranking up the mass while dialing down the radius, at some point the space-time curvature becomes so great that light will not be able to leave the point. This occurs when rs = r.
If you have and
rs is equal to r, you have a NaN.
The technical term for this is known mathematically as a singularity. What you know as the “singularity” at the center of a Black Hole stems from this relatively simple math.
Once the Schwarzschild radius is equal to the radius of the point in question, a Black Hole is formed. Theoretically, any massive object can become a Black Hole. The Schwarzschild radius of the Earth is about 9mm. So if you compress the radius of the earth to smaller than 9mm, the space-time curvature would become so great that no light would be emitted from it, as it would curve back in on itself. This is where the idea and name of the Black Hole originated — extreme space-time curvature as the result of a singularity within the Schwarzschild metric.
Meet Jocelyn Bell Burnell

At this point in time of the early 1900s, it was not believed that instances of Schwarzschild singularities could actually exist in nature. Singularities within equations are common, and this was purely a mathematical problem that Einstein had yet to solve. But as time passed without a solution, general relativity began to take on the reputation as an incomplete theory of gravity. It would stay this way for several decades, and sadly Einstein would not live to see its vindication. It wasn’t until 1967 when a graduate student made a discovery that would change everything.
Jocelyn Bell Burnell was a graduate student at Cambridge pursuing her Doctorate in radio astronomy. She and fellow students hand built a 4-acre radio telescope over the course of two years. When it came time to turn it on, what she found would launch her name into the annals of astronomical history. What showed up as regular, concise “beeps” on her graphical printer turned out to be the discovery of the first pulsar. Pulsars are neutron stars — stars so large that their collapse compromises the atoms themselves, forcing electrons into protons, leaving nothing but a big ball of neutrons left over. The mass remains the same, however, making neutron stars some of the most dense objects in the universe. With the discovery of the pulsar, the idea of Black Holes being real objects began to take foot in the halls of universities and observatories around the world. The hunt was on.
Black Holes Are Real, But Many Questions Remain

From this point forward, evidence of Black Holes began to pop up everywhere. They are believed to be at the heart of spiral galaxies, such as our own. A few years ago, the first gravitational waves were detected — emitted from the collision of two Black Holes. This year, the Event Horizons Telescope is hoping to produce an actual image of an event horizon, a non-physical location defined by the Schwarzschild radius.
There are still many questions about what goes on beyond that radius, however. Time plays a big role in this as time in and near a Black Hole is heavily dilated from our vantage point. But to the observer in the Black Hole, everything seems normal (all things considered). To us, a Black Hole appears virtually frozen in time — seconds passing within it are perceived as billions of years outside of it . There is also the question of mass. Black Holes are akin to giant galactic vacuum cleaners. What happens to all the mass that a Black Hole acquires?
The most interesting question is that of a more fundamental one. How does a mathematical singularity exist in our reality? How does one of the most massive objects in space become an “infinitely small point”… a point where nature figuratively divides itself by zero. Black Holes exist at the edge of our reality and outside the boundaries of our ability to logically describe. They are where physics ends, and speculation begins. So let’s speculate away in the comments! Free t-shirt to the first person who calculates the Schwarzschild radius of a Raspberry Pi!


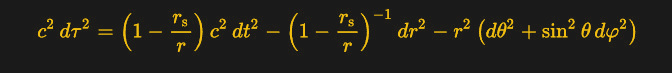














May I suggest you add the correct “Schwarzschild” to your spell checker? I see “Schwaszchild” and “Swartzchild” before eventually settling onto “Schwarzchild”. Even the built-in spell checker (English) of Firefox is marking those 3 as wrong.
Schwarz = black
Schild = shield
In one of the great quirks of historical irony, the most popular quote attributed to Newton — “If I have seen further it is by standing on the shoulders of giants” — might actually have been the mother of all passive-aggressive swipes at Robert Hooke. While it’s generally viewed as an eloquent demonstration of scientific humility on Newton’s part, the quote comes from a 1676 letter to Hooke, at a point where the pair were already arguing over proper credit for some work in optics. Hooke was commonly described as very short, even hunchbacked, and one theory is that Newton’s mention of “giants” was his way of saying Hooke had no influence on his work.
https://io9.gizmodo.com/5877660/was-robert-hooke-really-sciences-greatest-asshole
+1 It is not very Newtonian, except as an insult. He hated Hooke.
Raspberry pi Mass 0.072kg (http://cpc.farnell.com/raspberry-pi/raspberrypi3-modb-1gb/sbc-raspberry-pi-3-model-b-1gb/dp/SC14012)
Schwarzchild radius = 1.069e-28 m
Raspberry Pi 3 model B with a mass of 42g seems to have a Schwarzchild radius of 6.238 * 10^-29 meters. My bench vise wouldn’t squeeze it that tight!
Since we are talking about dividing by zero, we ought to look at the Schwartzchild radius of a Raspberry Pi Zero.
It has a mass of 9 g (without SD card), so the Schwartzchild radius is 1.337 * 10^-29 metres. Or 13 nonillionth of a metre, in round numbers. Less than a quarter of a Pi B!
that is quiet unlikely, for aesthetical reasons
Yet another example where the RasPi turns out to be verily 1337 :-)
(nitpick)People, do get your spelling act together! The man’s name is https://en.wikipedia.org/wiki/Karl_Schwarzschild .(/nitpick)
The Schwarzchild radius of a 42 grams Raspberry Pi is 6.238 * 10^-29 meters :) When do I get my t-shirt?
darn, did that really take me 5 minutes? *searching for delete button*
The Alpha Wolfram calculator does it for you. No need to dirty your sleeves on the blackboard.
“Free t-shirt to the first person who calculates the Schwarzchild radius of a Raspberry Pi!”
Challenge accepted, in python :)
All values pulled from Google:
from decimal import Decimal
c = Decimal(299792458)
G = Decimal(‘6.674E-11’)
M_1_A = Decimal(23) / 1000 # Mass of RPi model 1 A
M = Decimal(42) / 1000 # Mass of all the other RPis
Doing 2*G*M/c**2 I get roughly
6.23769E-29 meters
and for M_1_A I get:
3.41588E-29 meters
I can’t find an SI prefix for something this small, however the smallest I can find is yocto (10**-24). This would mean the Schwarzchild radius of a Raspberry Pi is 3.41588E-5 yoctometers or 6.23769E-5 yoctometers, depending on which model of Raspberry Pi you use.
My Hackaday calculator, calculated the radius as $radius = 555.
Coincidence…I think not.
I’m getting 4.158512672e-29 for the 42 gram Raspberry Pi 3.
Orbit of mercury (the element),
or the orbit of Mercury (the planet)?
Mercury (the god), obviously.
Oh, I thought they meant QuickSilver the superhero…
Back on USENET one man’s .sig was
“Black holes are where God is dividing by zero.”
B^)
when r equals r_s you usually have an Inf, not a NaN
Dividing by 0 is not inf. There are 2 ways to think of why it doesn’t.
If 1 / 0 == float(‘inf’) and 2 / 0 == float(‘inf’) then one can deduce that 1 == 2. That is reason 1.
Or we can take the limit. Say f(x) = 1 / x. If we take the limit to f(x) going closer and closer from the positive direction, then yes the limit to 0 of f(x) is indeed infinity. However, if we take the limit to f(x) from the negative direction, then the limit to 0 of f(x) is negative infinity. It is equally true to say that f(0) is negative infinity. Therefor we get 2 different values for the limit to 0 for f(x), so f(x) is undefined, not infinity.
int equal(float a, float b) { return a/0.f == b/0.f; }
int main(){
float a=1, b=2;
if(equal(a,b)) printf(“%f == %f\n”,a,b);
else printf(“Nope is full of bullshit\n”);
return 0;
}
// This is getting silly, I was joking with the IE3 floating point rules, because NaN is a concept that belongs to computers, not calculus.
Since zero is not signed, then the limit from each direction is not signed either. So, without a signed zero, how do you get two values instead of one? If plus zero and minus zero existed, I could grasp two values, i.e., plus infinity and minus infinity, but without it, with only unsigned zero, I can grasp only one, i.e. infinity.
Unless you define positive and negative infinity as the exact same thing, where space is curved into a loop, just like the higher dimensions in M-theory. Even looking at f(x) = 1/x in the two dimensional cartesian plane, it’s pretty obvious the plot line is continuous and the 2D flat-plane is not really 2D at all. Our mathematics is the limitation in it only describes the number system across the limited sample space of how we define it. In effect, no matter how we draw a 2D graph the axes can never even approach infinity – not even close – so we never can see the curvature that must be there. Kind of like how flat-Earthers refuse to believe the Earth isn’t spherical because they refuse to define it any other way.
Plus or minus?
“If you have \frac{1}{1-\frac{r}{r_{s}}} and rs is equal to r, you have a NaN.”
Since everything is pretty much “normal” as long as r is greater then r_s, it would seem that this formula attacks infinity from negative side (\frac{r}{r_{s}} being higher then 1) so it would be minus, but …
… in equation above that statement, it is \frac{1}{1-\frac{r_{s}}{r}}, so I’d say it is plus infinity after all.
Plus, for negative and positive r and rs. I concede a NaN when r=rs=0.
Infinity isn’t a number though, so it is NaN.
I tend to ignore local law, reality law and calculus laws and focus on the IE3 standards
Nope. On my state-of-the-art computer, when r equals r_s, I have an ‘?DIVISION BY ZERO ERROR’ followed by a ‘READY.’. I don’t know yet how to handle that type of result, but at least it’s not a NaN and not an Inf. :P
When the universe bluescreens.
Our multiverse is just a copy of the numerical system projection, gravity exists even in the numerical system! the theory of everything is based from asymmetry, intertwining and orientation “vector”! when you introduce motion to the abstract entities numbers , then its projection in our spacetime describes the dynamical system of a finite descrite asymmetrical lattice non tangled due to Paul Dirac belt trick generated by an so(3) transformation. the numbers are knoted and generate knoted orbitals! when the lattice degenerates it will simply describe the dynamical of a trefoil knot and its interconnection to the E8 lattice-singularity.
more detail link: peer-reviewed paper january, 2018 under the article ” the truth of mathematics & our asymmetrical multiverse of 11 dim” published in the international journal of theoretical and mathematical physics, sapub.org.
Wat?
http://article.sapub.org/10.5923.j.ijtmp.20180801.01.html
An actual entry. What it has to do with Black Holes is anyone’s guess?
Suspicious. This warrents further research.
From what I can see, the author and poster, [Salahdin Daouairi] is credited with the completion of the impressive THEORY OF EVERYTHING. I can’t find any other data to back it up. When I did a text search of the paper I found no mention of black holes.
The paper was published this year.
I smell somthing fishy…
Black Hole Singularities (BHS) are very common in our reality. There are an estimated 1.7 BHS’s in our own galaxy. It is our hope that the CERN will soon create one. R = 2GM/c2. For instance, the singularity of Earth is 8.8 mm.
This is… total nonsense. That’s the Earth’s Schwarzschild radius – if the Earth got compressed inside it, it would form a black hole. But black holes don’t have singularities at the Schwarzschild radius. They have one at their *center*, and the reason for that is that general relativity has no small-scale quantization: it’s a smooth theory, so you can infinitely compress everything.
Schwarzschild (“Black Shield”) is misspelled as Schwarzchild (missing an s) several times in the article.
So, are you Eliot and Al’s long lost brother?
B^)
No, no relation. And there are two ‘l’s in Elliot :)
Fixed. Thanks!
One interesting thought experiment is the hollow black hole: A solid shell of ordinary matter that is smaller than its own Schwartzchild radius, with a hollow center. Like all hollow spherical shells, the gravity the shell on the inside would cancel out. As the Schwartzchild radius gets bigger, the overall density gets smaller. I’ve never bothered to calculate the stresses on such a shell to see if such a thing could be made of ordinary metals instead of weird collapsed matter.
With a creamy caramel center!
A rotating black hole might have ring shaped singularity with no center also, that is, if matter exists inside black holes. at all? The mass of a black hole can consist of photons, angular momentum, or sort of sub quantum degenerate matter it will look the same on the outside. It can also be that time dilation slows everything sufficiently down, so that the original collapsing star core is still collapsing in ultra slow motion together with whatever material it has accreted since, and a black hole only lasts a pico second in its own time frame before it bounces back and evaporates? Quantum mechanics is also having a shot at Black holes and the Current EP=EPR Quantum thermodynamics Theory suggests that there is an receding inside event horizon and space is growing inside the black hole, like how we observe our universe from the inside. This is the holographic principle turned on its head in the sense that the natural laws dictates that sufficient complexity in the high energy particle shower inside a black hole, forces the creation of more space to keep a record of what is happening, i.e. Causality preserved and information never lost ptoblem.
I love black holes, They are the simplest physical object to describe in the universe, but extremely challenging if you ask what they are!
Do any black holes exist? Or are they all in the process of forming?
Your guess is as good as any’s.
Yeah, doesn’t work like that. Think about it. If you’ve got no matter from r=0 to r=r_inner_shell, matter from r_inner_shell to r_outer_shell, and the Schwarzschild radius for the ensemble is bigger than r_outer_shell, it’ll collapse.
Why? Because while there’s no gravity inside r=0 to r=r_inner_shell, there will be gravity from r_inner_shell to r_outer_shell. There will be some r (between the inner/outer edges) such that there is enough matter inside that it is at *that* Schwarzschild radius. Which means it must fall inward, no matter what. Then the shell beyond that, then the shell beyond that… etc. etc.
Good description of some of the most advanced hacking humanity has managed to perform, with examples. But, there should have been a tie-in to the 5 yr old hacking with legos, the 10 yr old with an erector set, the 14 yr old with a lawnmower engine and some wheels, and the parent’s solution to the pain of a lego underfoot. It’s all hacking. Just different subjects at different levels. Heck, even chimps and crows do it with a stick to get grubs to eat.
I kept waiting for the article to connect this all to us.
What happens when r < rs and the equation goes negative? Will all the light travel to the center of the singularity?
All paths go towards the centre of singularity, pretty much as time always goes in one direction in our side of the horizon.
Universe sucking singularity at one point in time in the future, with the other end in the distant past being called The Big-Bang.
The ridiculous part is that inside the Schwarzschild radius, *time* no longer necessarily goes in ‘one direction’. That’s a bit science-fictiony (the common statement is ‘time and space switch places’) but the simple observation is that inside the black hole while falling to the center, you can encounter objects that fell in millions of years before you (from the outside perspective) as well as objects that fell in millions of years after you (again, from outside).
It’s also worth pointing out that for a large enough black hole, falling through the event horizon (= Schwarzschild radius) is completely benign: the tidal forces can be made arbitrarily mild, and supermassive block holes like this do exist. So it’s not an ‘academic’ point in the sense that you really could do this… although we’d never know about it.
is the Schwartzchild radius relative to your distance? with extreme space/time dilation, wouldn’t the closer you get to the black hole, the smaller it becomes?
“What happens to all the mass that a Black Hole acquires?” White holes in another reality? Mass changed to energy, smeared across the cosmos?
Rather smeared across the mycelium network
The mass that the black hole acquires stays in there, exerting gravity on the stuff outside. If it went somewhere else after getting squished, the black hole wouldn’t have the gravitational force it takes to be a black hole.
It’s at least “effectively” still there, modulo Hawking radiation. As in, it couldn’t spit out into our own Universe or something like that – in order to make a multiply-connected setup like that (with a traversable throat) you need something with negative energy density to “push” the throat open, and negative energy density material (that you can collect) doesn’t seem to be common here. But when you start asking about “white holes in another reality,” who the hell knows. I can always fudge the rules of the other Universe to make it work, after all.
” If it went somewhere else after getting squished, the black hole wouldn’t have the gravitational force it takes to be a black hole.”
It’s a little more complicated than that. Gravity is curvature, and curvature is gravity. So if there’s some way to maintain the same *curvature* (as viewed from the outside) without the matter actually being collected at the singularity, maybe. It’d be a seriously contrived setup for it to work, though. Traditionally if you imagine a black hole being connected to another black hole (which isn’t a white hole, mind you, it’s just two connected black holes such that you’re trapped inside the combined event horizon of the two), whenever you drop any matter into it, the “throat” collapses (because gravity’s attractive). To make it work, like I said, you’d need some amount of negative energy density matter which can effectively fight against the matter dropped into it. In that case, it’d be super weird, because the exotic matter would compensate for the matter being on the “wrong side” and would end up making everything look exactly the same. Drop *enough* matter through and everything would eventually go poof.
(note that it’s insane there are ridiculous numbers of papers on traversable black hole throats given the fact that they almost certainly don’t exist)
As some of the other commenters have said the Schwarzschild radius of a raspberry pi would be something in the order of 10^-29, that’s less than a Planck length, so I’d say it’s not possible.
And now we’ve really reached the limit. ;-)
” Apart from particle physics, almost all scientific discovery throughout recorded history has been made via experiment and observation.” Begs some explanation.
A Black Hole is something you DON’T want in your laboratory.
With how fast they evaporate, I wouldn’t be worried about any black hole in a laboratory.
Since we have no direct observations of black holes, you should not be too quick to state with certainty how a artificial tiny one would behave, it would “suck” to be wrong drop one and have the rest of the planet absorbed.
Curse you, OlsssssSLUUURP!
@Ostracus
At least my name would echo for all of eternity ;-)
Thats what she said!
The question is, why does the author exclude particle physics from experimentation and observation?
Can I get a t-short anyway? Think of it as a participation trophy.
T-short?
How do I measure that?
I think you mean to compress the mass of Earth to a radius of 9mm. Other than that, this has actually been enlightening.
Just because black holes exist doesn’t mean that there has to be a singularity at their centers. We simply don’t know what is inside a black hole. I tend towards thinking that the concept of a singularity is a byproduct of the mathematics used. At the core of calculus is the concept of infinitesimals and when it is applied to physics there is the underlying assumption that space can be divided into ever smaller pieces without limit (I.e. space is continuous). If space is discrete and not continuous, and quantum physics seems to indicate that to be the case, then there would be no singularity. Exactly what happens at the limit is unknown and maybe unknowable.
I like to think that the amount of information in the universe is bounded and so space is inherently discrete. Interestingly, even something as simple as Pythagoras’ theorem can be hard to prove in discrete space so coming up with the mathematics for a discrete space that is consistent with the observed universe is challenging.
i might as well through my two bits in as well. Perhaps someone will find them interesting… Bahá’u’lláh, the Founder of the Bahá’í Faith, a fairly recent religion (1863) states that the universe is infinite in its range and scope and that it has always existed since its Creator can never be imagined without a creation. Maybe everything that’s going down the black holes is going to the same place and accumulating in anticipation of the next Big Bang?
The Big Bang theory doesn’t agree with that – in the general relativity versions, spacetime and the universe began with the big bang, and before that there wasn’t any there there. If there’s a Creator, and a creation, that would have actually happened some time, or it wouldn’t have been a creation, just another thing, and any difficulties in imagining a Creator who hasn’t created things yet are limitations of your imagination.
Meanwhile, the stuff that fell into black holes stays there, exerting gravity on things.
“The Big Bang theory doesn’t agree with that ”
Yeah, actually, it doesn’t say anything about that at all. As with the center of a black hole, the Universe taken back to time = 0 in general relativity is a singularity, which means the theory breaks down at that point. It actually breaks conservation of energy because, by Noether’s theorem, it represents a point where the Universe isn’t symmetric under time translation. Which is why it’s unsurprising that any theory which is developed to “work” at those scales (and still have conservation of energy) ends up effectively ‘erasing’ the idea that “there’s nothing before this” and getting rid of the singularity.
“Meanwhile, the stuff that fell into black holes stays there, exerting gravity on things.”
Meh. Same idea – it’s a singularity, so the theory doesn’t actually say what the heck happens there. I’m sure someone could come up with some weird theory where, in fact, the matter actually accumulates in one place (i.e. all black holes multiply connect) with the “effective” mass seen at each black hole being the amount of matter that’s fallen in. But that’s the innate problem with black holes: because the event horizon prevents any internal information from leaking out, until we can really confirm/observe something like Hawking radiation, it’s hard to imagine understanding the interior of a black hole at all.
Per the old Movie, Black Hole, if one gies through a black hole and emerges elsewhere, would the bkack hole not do the same? If matter and energy are conserved, the back hole would emerge somewhete else, perhaps not compacted, any longer. Now add to this, string-theory and expanding (for now,) universe, which possibly… re-bangs. In composting, outside material is circulated to the inside. This does that, but full circle, until the end of times.
the rs for a 42gPi3B would be 0.0000000000000000000000000620181m
See the calculation here:
https://cdn.hackaday.io/images/9629271517891302552.jpg
The rs for a 42gPi3B would be 0.0000000000000000000000000000620181m
meaning 6.2 *10^-29m
See the calculation here:
https://cdn.hackaday.io/images/9629271517891302552.jpg
how do I correct this?
https://cdn.hackaday.io/images/7860881517891988156.jpg
“The technical term for this is known mathematically as a singularity. What you know as the “singularity” at the center of a Black Hole stems from this relatively simple math.”
Yeah, no. This is wrong.
The singularity at the center of the black hole is at r = 0, not r = r_s. In fact, *nothing* goes singular at r = r_s except the coordinate system. The standard example of this is the longitude of the North Pole: if you have something moving north, once it crosses the North Pole its longitude flips immediately 180 degrees around, so it looks like a singularity, but it’s just a bad coordinate system.
In this case, the problem is that you’re assuming that you’ve still got static coordinates inside the Schwarzschild radius, which of course you know you don’t have. That is, you can have something at (t, r, theta, phi) = (1, 1, 0, 0) and you can have something else at (0.5, 1, 0, 0) and something at (1.5, 1, 0, 0): there’s no connection between the ‘t’ coordinate and the spherically symmetric ‘r’ coordinate. Inside the Schwarzschild radius, things always fall to the center, so you *can’t* have that ‘static’ setup. It’s not possible to move from (0.5, 1, 0, 0) to (1, 1, 0, 0).
Lemaitre and others realized this shortly afterwards and derived new coordinate systems which avoid that coordinate singularity (by coupling the radial coordinate and the time coordinate), and everything is happy-hunky-dory across the Schwarzschild radius.
The singularity at the center of the black hole actually comes from the term in front of the *time* coordinate: (1 – rs/r). If you plug in “r=0”, *that* blows up as well. And *that* one doesn’t go away with new coordinates.
Think about it… Why do we think that we are outside the singularity? We might actually be inside the singularity. And what looks to us as to BE the singularity, might actually be the ‘outside’, and not a singularity at all.
Hey presto. And we find that even if our math is an objective language for describing things, our equations are still derived from what we see, and are not objective at all. Our math describes a singularity as a point mass with infinitely small size. Well, that’s what we see, and what we imagine a singularity to be. But looking at it from inside the singularity, it will all be different. So we’re staring ourselves blind on equations with divisions by zero and NaN’s and infs, and whatever. While if we would make our equations from a different point of view, there might be no singularity at all. :)
There is no physical singularity at the Schwarzschild radius. There is nothing physical separating “outside” the event horizon from “inside.” The reason we know we’re not inside a giant black hole is because there’s no stuff from outside falling in.
The physical singularity in a black hole is at the center, at r=0. There’s no “inside”. It’s just a point.
If we think the black hole as a rupture of time caused by gravity and the other side of the black hole to be a big bang of another universe in cosmos we would effectively be inside of some singularity.
No, because the singularity inside the black hole has matter falling on it constantly (so its mass increases), and our universe doesn’t have that. Even if the black hole in the other Universe is in a totally empty cosmological horizon, it’s then *losing* mass due to Hawking radiation, and again, our universe doesn’t have that.
What we mean to define: (when anyone of us said) singularities / black holes: is *boundary conditions* we can now define them as: *specific geometric harmonic resonance ratios*. It is very very important cause: in an *electric universe* (which is very pragmatically wonderful) IT IS GEOMETRY (energy flow of consciousness) wich enables us yogis to do: https://plus.google.com/u/0/communities/114141235936810104482
here is the ancient hindu science: https://sites.google.com/site/theconsciousnessstates/11-unit-dimensions here is the bridge we are building into the today academic math:
https://drive.google.com/file/d/1PWDmo6uRfGOtoLra579pEYTi6WrzUdKq/view?usp=sharing https://docs.google.com/presentation/d/e/2PACX-1vQAZ5sCQFNhWkyAnoK0oi_ibbaFE14QmKuENkjC8pYSi7RmxlFlkwTpIfmgYa0jmNfPn7JF85aIGcO7/pub?start=false&loop=false&delayms=3000&slide=id.g1b7c4b6f2b_0_0
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
Symmetry is part of the language of nature.
From the molecular level on up: Many animals and plants exploit symmetrical shapes as a way of standing out against the chaos of their landscape.
This brain (matter) is perhaps the very best example for holo-fractal architecture of nature.
It is very very important cause:
fractal mathematics teaches the mathematics of infinite compression because the principle of the golden mean allow for the addition and multiplication of any kind of waves (also charge and energy)
golden ratio is self-similarity (fractality) optimized
golden ratio enables perfected feedback (information exchange) between scales in nature (e.g. micro and macro cosmos)
the idea of symmetry is vital all of this
PROOF:
1. The holo(fractal)graphic ratio relationship of quantum vacuum fluctuations (QVF)
has been found to PREDICTS the charge radius of the proton with more precision than has ever been achieved before.
2. golden ratio (phase conjugate) times planck length & time PREDICTS:
the brainwave (alpha / beta) frequencies of peak perception / bliss
voltage generated by a fresh egg or a pine cone apparently from the gravity field by being a fractal attractor for weak capacitancemultiple exact radii of hydrogen
the exact only 2 frequencies which motorize photosynthesis
virtually exact duration of the Earth year and Venus year
and much more