We are unabashed fans of [The History Guy’s] YouTube channel, although his history videos aren’t always about technology, and even when they are, they don’t always dig into the depths that we’d like to see. That’s understandable since the channel is a general interest channel. However, for this piece on James Clerk Maxwell, he brought in [Arvin Ash] to handle the science side. While [The History Guy] talked about Maxwell’s life and contributions, [Arvin] has a complementary video covering the math behind the equations. You can see both videos below.
Of course, if you’ve done electronics for long, you probably know at least something about Maxwell’s equations. They unified electricity and magnetism and Einstein credited them with spurring one of his most famous theories.
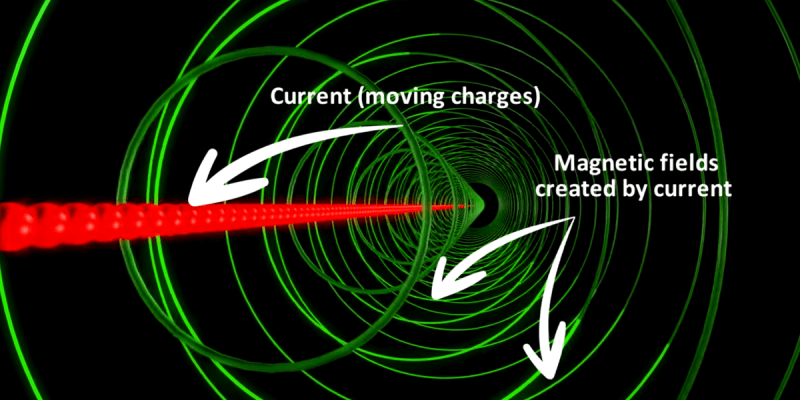
Deriving Maxwell’s equations is a math nightmare, but [Arvin] doesn’t do that. He uses some amazing graphics to explain how the equations relate electricity and magnetism. A great deal of our modern world — especially related to any sort of radio technology — builds on these four concise equations.
One thing we didn’t realize is how wide-ranging Maxwell’s interest were. He contributed to astronomy by explaining Saturn’s rings, derived statistical laws about gasses, and worked on color vision, including creating the first light-fast color photograph. He also contributed to thermodynamics, control theory, and optics. Those were the days!
We really enjoyed the way the two videos support each other. Understanding the math is a big deal to us, but understanding the man’s life and the context he lived in is pretty interesting, too. We hope we see more such collaborations.
Not that we don’t do our part to try to tell technology history with a bit more depth than a typical history book. Do you remember [Rufus Turner]? We do. We’ve even had a few debates over who really invented radio. If you want more of that, you can always browse our history tag.















As I understand it Maxwells equations as well as being intrinsically relativistic, is readily quantised and the symmetry he “shoehorned” in is a good example of gauge symmetry.
Wonderful serendipity?
It’s probably “a complementary video”, not “complimentary”.
Although Maxwell definitely deserves compliments, no questions.
Grammarly is utterly hopeless then, if I were to put on my lit-crit hat, I’d also question a few comma placements, notice incorrect singular/plural use, and wonder why it didn’t notice Einstein is misspelled. ( I know it’s a proper name, but being a famous person, I’d want something that is supposedly an uber-spellchecker to notice.) In fact if it is the case that the entire Hackaday writing staff has been using grammarly that would explain what looked like a sudden deterioration in writing quality as technical terms have been replaced with homophones and other random garbage has crept in which corrupted meaning.
Thanks. Fixed.
Well you can watch the video for free…
I’ve always meant to spend some time trying to understand how to apply Maxwell’s equations (and possibly learn how to use them to simulated 3D space of maybe 1000x1000x1000 voxels for an iterative non-intuitive approach for antenna design), but I have to admit that the maths in those four concise equations has always scare the hell out of me. Is there less concise version with hopefully hell of a lots more equations that is far more approachable, to the mathematically illiterate (I did study three dimensional partial differential complex equations a long long long long time ago, but that maths hurt my head back then as well).
“Is there less concise version with hopefully hell of a lots more equations that is far more approachable,”
Uh… no? Electromagnetism at this level is the bane of physics students in graduate school: the seminal text (Jackson’s Classical Electrodynamics) is usually considered a weed-out class in grad school.
Solving Maxwell’s equations in a simulated 3D space is Not Easy. The typical way to do it is with finite-difference time domain (FDTD) simulations, which can be very expensive (both computationally and cost-wise).
There is an open-source free FDTD simulation called MEEP, but without access to grid-scale computing you’re likely to struggle to use it for iterative design due to memory/computing constraints.
To scare you even more, Maxwell’s equations aren’t even really 4 equations: relativistically, they’re just one. They’re just saying that the wave (d’Alembert) operator of the electromagnetic field is defined by the 4-dimensional electromagnetic current. Or, in far fewer words: the electromagnetic field is wave-generated by charges and currents. That’s it.
Yes, the reason the F-117 and related projects are so angular is BECAUSE it’s a problem modelling Maxwell’s equations in 3D. They had to do the bulk of it in 2D… and this is people with access to the supercomputers of the time, well into the 80s, probably most of the 90s. Don’t think it’s been long since they could do it without dimming lightbulbs in the whole rest of the state.
With exascale computing we could do it.
https://www.anandtech.com/show/15661/folding-at-home-reaches-exascale-1000000000000000000-operations-per-second-for-covid-19
“Yes, the reason the F-117 and related projects are so angular is BECAUSE it’s a problem modelling Maxwell’s equations in 3D.”
The reason the F-117 and related projects are so angular is BECAUSE IT WORKS.
Yes, but the flat facets and sharp joints compromise flight characteristics considerably. Later stealth projects aren’t nearly as angular because there was sufficient computing power by then to allow the much more desirable non-faceted stealthy surfaces and cross-sections.
We all can create stealth equipment. If the stealth bomber or DDG Navy destroyer were made of mirrors you would see very little of yourself. This contributes to the Grand majority of the reduced radar signature. In fact the Aeigis DDG destroyer uses no radar absorbent paint(believe me I have painted the USS Benfold DDG-65 many times), and when seen from another ship or aircraft looks like a small ship or nothing at all depending on the angle. The ships hull is more traditional and gives away some of the cross section.
look at the stark contrast when you compare it to the B-2…these are less then 2 decades apart…
Get a copy of the paperback “Div Grad Curl and All That” and a used copy of David Griffiths ‘Introduction to Electrodyanamics. On YouTube check 3Blue1Brown’s videos.
All these are great!
Also, the videos by Eugene Khutoryansky on YouTube are really amazing and cover EM.
As Jesse Jenkins alluded to, Oliver Heaviside already simplified Maxwell’s equations. His simplifications are commonly referred to as “Maxwell’s equations.” From the Wikipedia article on Heaviside: “In 1884 he recast Maxwell’s mathematical analysis from its original cumbersome form (they had already been recast as quaternions) to its modern vector terminology, thereby reducing twelve of the original twenty equations in twenty unknowns down to the four differential equations in two unknowns we now know as Maxwell’s equations. “
I suppose Maxwell could (should?) be considered a polymath. In this day of specialization it’s hard to find them.
He neglected monopole current. If only we had a loop of some material that would support monopole current, we could have a transformer that would work on DC! Was he friends with Tesla or something?!
=P
Haven’t looked at the videos yet but read an interesting book a while back called The Maxwellians. My recollection is Faraday independently captured the data. Maxwell developed ~16 equations and a team of others (Heaviside, Hertz, etc) distilled it to the 4 equations. A bit more of teamwork?
Interesting how after Thomas Young in 1827 rejected the theory that light is made of material particles moving through empty space in favor of the alternative theory of a medium of material particles that collide off each other in a transverse wave motion, way back in 1864 Maxwell adopted and piled on his more complex theory on top of that- viewing light not as just a single transverse wave in a material particle medium, but as a dual transverse wave. see Maxwell’s originally published graphic at Google books: https://books.google.com/books?id=gmQSAAAAIAAJ&printsec=frontcover&dq=editions:0w8AGC9HxP35YR6Uk9&lr=&as_brr=1&hl=en#v=onepage&q&f=false. I am fascinated by the alternative theory that lost- the view that light is more like a tennis ball moving through empty space rebirthed very briefly by Descartes in his Le Monde, and amplified by Newton in the 17th and 18th centuries, it is amazing to me to think that maybe way back on the timeline a terrible mistake was made resulting in a nearly 200 year dim age in the human understanding of light. I think it is healthier to keep an open mind and entertain the main alternative like we do a two-party system in government.
You’re really making a distinction where there isn’t one. Think about the surface of a drum: a drum can only admit certain standing wave patterns on it. If you try to establish some other pattern, it won’t work. So the drum’s excitations are quantized: they can only be established in certain fixed modes.
Light, like everything else that carries energy/momentum, is the same thing. Just imagine the 4D electromagnetic field as the surface of the drum, and light as the quantized excitation of it.
Don’t understand your point but I’m going to go out on a limb and say “No.”
That sounds like nonsense.
sorry link to image is: http://books.google.com/books?id=gmQSAAAAIAAJ&printsec=frontcover&dq=editions:0w8AGC9HxP35YR6Uk9&lr=&as_brr=1#PPA390,M1
Thanks for posting this! Dare I look forward to a similar piece on Heavyside?
But here’s a question: [Why] [do] [you] [insist] [on] [putting] [names] [in] [brackets] [?]
It’s a stylistic holdover from the days when HaD articles were all fully lowercase, so it was harder to parse out proper nouns.
Nice article, I live a couple of miles from the ruins of his family home at Glenlair near Kirkpatrick Durham.
Those are Oliver Heaviside’s rewrite of Maxwell’s Equations.
Which are good (in an engineering sense, are valid for) situations involving EM where *nothing is moving*.
(ie, antennas, situations where nothing* is in motion).
* or at least to a good approximation.
In particular, if you want to deal with electromagnetic actuators or motors of any kind, do not use these, because they are wrong. (trivially — Faraday’s law requires the Total (aka ‘Material’) derivative of B wrt time).
Just use Faraday’s or Ampere’s directly for designing electric motors / actuators.
You can kind of make M-E kinda sorta work with a pretty big caveat for moving things — but it’s really a nasty hack, and precludes getting an actual mathematical solution for the results (trajectories) that you want. This is where you have to freeze time, solve for B and E, then ‘switch’ to Newtonian physics, using Lorentz’ law to solve for the force on the particle you’re actually interested in, update acceleration, step time, update velocity, position, then switch back to consider that both charge density and current density may now be different (because, again, SOMEthing is moving, or at least, it’s not insignificant about the place where the things you want to be moving actually are).
Note, that if you’re building a particle accelerator which will never achieve a very high space charge, then the approximation that nothing is moving is actually quite good, so it will actually mostly work. Obviously better in high energy particle accelerators where you’re just trying to achieve the highest possible particle energy. Which, again, is much easier so long as you keep space charge (beam line current) low.
Oh, and note that the average actual electron velocity in a conductor is usually in the range of ~ mm / hour for even quite large currents, so again, good for high power antennas and things of that nature (like waveguides etc, or unintentional EMI / EMR from circuits). Quite high powers are OK, so long as — nothing has a velocity.
Which is why Einstein spent his later years in such stress. Poor guy.
But, as a person with training in this thing, it always pisses me off when people hold up these (which Maxwell would have hated, he and Heaviside would not have gotten along well — they would have fought over Quaternions for sure) as somehow being the touch-stone for any engineering involving the magical ‘force of nature’ that EM is.
They’re not — except, again, if nothing is moving right now.
For a really interesting read (/ super huge rant) on this, Look up Thomas E Phipps Jr’s books.
Particularly interesting also is how the 3d stereographic projection of 4D solid unit hypersphere rotations look a heck of a lot like how E and B are related.
This involves using the ‘imaginary’ part of a quaternion as x,y,z spatial axis, and just using the ‘real’ part as a sort of ‘sump’ to hold the rest of a unit vector that might not be ‘in use’ for representing an orientation change. (makes ‘real’ and ‘imaginary’ and even more ironic way to name those parts — it really does seem that all real spatial dimensions we are familiar with are actually themselves ‘imaginary’, and not really ‘real’. But swapping those two is just a definition change, albeit an amusing one — when we count a number of actual things, we’re really imagining a number — the traditionally ‘real’ part ).
Also how Octonions (8D extended quaternions — basically a real part and seven mutually perpendicular extra imaginary dimensions, with their own special order-of-operation rules and equivalences) seem to map to the other ‘fundamental forces’. ( ref: https://www.quantamagazine.org/the-octonion-math-that-could-underpin-physics-20180720/ )
The way I like to think of it is, perhaps space naturally is higher dimensional, and the three we experience are actually just three of a higher set, much like quaternions are exploitable for mapping really nicely to how we experience rotation in 3d. Matter as we know it, along with our familiar lowish energy EM forces seem to be constrained to three, with movement in the others being somehow very tightly constrained (except at very high energy densities where sufficient energy is available to ‘free up’ more degrees of freedom — much like how in thermodynamics, heat capacity for different materials tends to increase in jumps with increasing temperature as more ‘degrees of freedom’ get un-frozen).
This video utterly fails to mention Maxwell’s invention of Quaternions, or the controversy of how they were hated and suppressed by people who weren’t smart enough to see their elegance, or their incredibly practical application. People like… Oliver Heaviside…
The really sad part is how young Maxwell died.
Who knows where we’d be now if he’d only lived to a typical age for his peers.
Also, the speed of light ‘c’ didn’t come about that way either. It came about from the Telegrapher’s equations for transmission lines, and specifically due to the emergence of electronic engineering due the problems of signal reflection in long telephone lines. It’s slower, but exactly because absolute permittivity and permeability are higher in anything other than a vacuum!
Now think a little about the refractive index in transparent materials…. M-E’s are actually good for optics as well! It’s how you design anti-reflective thin-film coatings, as well as super-reflective thin film wavelength-specific (ie, laser line) coatings too.
And yes, 1/4 wave for impedance matches (no reflections) and 1/2 wave for full-reflection coatings applies just as you’d expect.
“This video utterly fails to mention Maxwell’s invention of Quaternions..”
I always thought that William Rowan Hamilton invented quaternions?
https://en.wikipedia.org/wiki/Quaternion
You sir, are correct.
And I, Am wrong in that detail. It was Hamilton. (I am really *really* bad with remembering names…) I got the two conflated. Doh.
Maxwell would surely have been aware of them, especially since he was personally tutored by Sir William Hamilton, and I’m quite sure he had a strong intuitive grasp of them.
His conception for his electromechanic field equations was all based on a concept of vortices. Nothing if not rotational in nature.