We are often struck by how often we spend time trying to optimize something when we would be better off just picking a better algorithm. There is the old story about the mathematician Gauss who, when in school, was given busy work to add the integers from 1 to 100. While the other students laboriously added each number, Gauss realized that 100+1 is 101 and 99 + 2 is also 101. Guess what 98 + 3 is? Of course, 101. So you can easily find that there are 50 pairs that add up to 101 and know the answer is 5,050. No matter how fast you can add, you aren’t likely to beat someone who knows that algorithm. So here’s a question: You have a large body of text and you want to search for it. What’s the best way?
Of course, that’s a loaded question. Best can mean many things and will depend on the kind of data you are dealing with and even the type of machine you are using. If you are just looking for a string, you could, of course, do the brute force algorithm. Let’s say we are looking for the word “convict” in the text of War and Peace:
- Start with the first letter of War and Peace
- If the current letter isn’t the same as the current letter of “convict” then move to the next letter, reset the current letter in “convict” and go back to step 2 until there are no more letters.
- If the current letters are the same, move to the next letter of convict and, without forgetting the current letter of the text, compare it to the next letter. If it is the same, keep repeating this step until there are no more letters in “convict” (at which point you have a match). If not the same, reset the current letter of “convict” and also go back to the original current letter of the text and then move to the next letter, going back to step 2.
That’s actually hard to describe in English. But, in other words, just compare the text with the search string, character by character until you find a match. That works and, actually, with some modern hardware you could write some fast code for that. Can we do better?
Better Algorithms
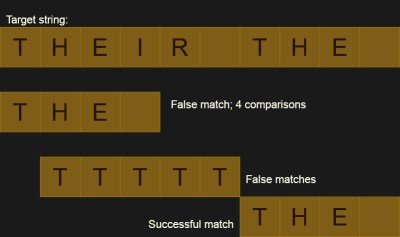
Again, it really depends on your definition of better. Let’s assume that the text contains many strings that are almost what we are looking for, but not quite. For example, War and Peace probably has many occurrences of the word “the” within it. But it also has “there,” “then,” and “other” all of which contain our target word. For the word “the” that isn’t a big deal because it is short, but what if you were sifting through large search strings? (I don’t know — DNA genome data or something.) You’d spend a lot of time chasing down dead ends. When you discover that the current text has 199 of the 200 characters you are looking for, it is going to be disappointing.
There’s another disadvantage. While it is easy to tell where the string matches and, therefore, where it doesn’t match, it is hard to figure out if there has been just a small insertion or deletion when it doesn’t match. This is important for tools like diff and rsync where they don’t want to just know what matched, they want to understand why things don’t match.
It was looking at rsync, in fact, that led me to see how rsync compares two files using a rolling checksum. While it might not be for every application, it is something interesting to have in your bag of tricks. Obviously, one of the best uses of this “rolling checksum” algorithm is exactly how rsync uses it. That is, it finds when files are different very quickly but can also do a reasonable job of figuring out when they go back to being the same. By rolling the frame of reference, rsync can detect that something was inserted or deleted and make the appropriate changes remotely, saving network bandwidth.
In Search Of
However, you can use the same strategy for handling large text searches. To do this, you need a hashing algorithm that can put in and take out items easily. For example, suppose the checksum algorithm was dead simple. Just add the ASCII codes for each letter together. So the string “AAAB” hashes to 65 + 65 + 65 + 66 or 261. Now suppose the next character is a C, that is, “AAABC”. We can compute the checksum starting at the second position by subtracting the first A (65) and adding a C (67). Silly with this small data set, of course, but instead of adding hundreds on numbers each time you want to compute a hash, you can now do it with one addition and subtraction each.
We can then compute the hash for our search string and start computing the hashes of the file for the same length. If the hash codes don’t match, we know there is no match and we move on. If they do match, we probably need to verify the match since hashes are, generally, inexact. Two strings might have the same hash value.
There are, however, a few problems with this. If you are just looking for a single string, the cost of computing the hash is expensive. In the worst case, you’ll have to do a compare, an add, and a subtract for each character, plus maybe some tests when you have a hash collision: two strings with the same hash that don’t actually match. With the normal scheme, you’ll just have to do a test for each character along with some wasted tests for false positives.
To optimize the hash algorithm, you can do fancier hashing. But that is also more expensive to compute, making the overhead even worse. However, what if you were looking for a bunch of similar strings all with the same length? Then you could compute the hash once and save it. Each search after that would be very fast because you won’t waste time investigating many dead ends only to backtrack.
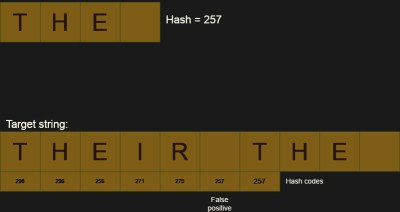
My hash algorithm is very simple, but not very good. For example, you can see in the example that there is one false positive that will cause an extra comparison. Of course, better hash algorithms exist, but there’s always a chance of a collision.
How much is the difference using this hashing strategy? Well, I decided to write a little code to find out. I decided to ignore the cost of computing the search pattern hash and the initial part of the rolling hash as those will zero out over enough interactions.
Convicted
If you search for the word “convict” in the text of War and Peace from Project Gutenberg, you’ll find it only occurs four times in 3.3 million characters. A normal search had to make about 4.4 million comparisons to figure that out. The hash algorithm easily wins with just under 4.3 million. But the hash computation ruins it. If you count the add and subtract as the same cost as two comparisons, that adds about 5.8 million pseudo comparisons to the total.
Is that typical? There probably aren’t too many false positives for “convict.” If you run the code with the word “the” which should have a lot of false hits, the conventional algorithm takes about 4.5 million comparisons and the adjusted total for the hash algorithm is about 9.6 million. So you can see how false positives affect the normal algorithm.
You’ll note that my lackluster hashing algorithm also results in a large number of false hash positives which erodes away some of the benefits. A more complex algorithm would help, but would also cost some upfront computation so it doesn’t help as much as you might think. Nearly any hashing algorithm for an arbitrary string will have some collisions. Of course, for small search strings, the hash could be the search string and that would be perfect, but it isn’t feasible in the general case.
The code doesn’t save the hashes, but suppose it did and suppose the false positive rate of the first search is about average. That means we save a little more than 100,000 comparisons per search once the hashes are precomputed. So once you have to search for 60 or so strings, you break even. If you search for 600 strings — but don’t forget, they all have to be the same size — you can save quite a bit over the easy comparison code.
I didn’t actually time things, because I didn’t want to optimize each bit of code. In general, fewer operations are going to be better than more operations. There are plenty of ways to bump the code’s efficiency up and also some heuristics you could apply if you analyze the search string a little bit. But I just wanted to verify my gut-level feel for how much each algorithm spent on searching the text.
Reflections
I originally started thinking about this after reading the code for rsync and the backup program kup. Turns out there is a name for this, the Rabin-Karp algorithm. There are some better hash functions that can reduce false positives and get a few extra points of efficiency.
What’s my point? I’m not suggesting that an RK search is your best approach for things. You really need a big data set with a lot of fixed-size searches to get an advantage out of it. If you think about something like rsync, it is really using the hashes to search for places where two very long strings might be equal. But I think there are cases where these oddball algorithms might make sense, so it is worth knowing about them. It is also fun to challenge your intuition by writing a little code and getting some estimates of just how much better or worse one algorithm is than another.
















Hash functions…. Wikipedia has many pages about it, and https://hackaday.io/project/178998-peac-pisano-with-end-around-carry-algorithm explores new approaches :-)
For the case of short words in a large text, a SIMD approach is probably more effective. Don’t bother trying to match for all letters of the word, instead pick the least common letter and compare a bunch of bytes against it at once. If you find a match, only then investigate more closely. On a multiprocessor system, the investigation of possible matches can be delegated to another core. This can easily process the data as fast as the system can fetch it from RAM.
If the original text is 3.3 million characters, to search for “convict”, and you want to minimize comparisons:
The probability of finding “C” is 2.8%, so 3.3*.028 million hits on the comparison for the 1st character.
“O” will be the next letter randomly 7.5% of the time, “N” is 6.7% of the remaining time, “V” is .98%.
3,300,000 + (3,300,000*.028) + (3,300,000*.028*.075) + … => 3.4 million comparisons.
(The presence of punctuation and other non-alphabetic characters make the actual frequencies *less* than standard frequencies. Also, this is caseful search, and when actually searching for words you may want caseless.)
Sorting “convict” by letter frequency and looking for the least common letters first:
3,300,000 + (3,300,000*.0098 “V”) + (3,300,000*.0098*.028 “C”) … => 3.3 million comparisons.
The issue is one of fundamentals. The RK algorithm assumes “Each comparison takes time proportional to the length of the pattern”, which is not true of simple text search. Since one (and only 1) English letter has a frequency of more than 10%, you can reduce your search space by at least a factor of 10 on each consecutive letter.
(Note: Information content of English is about 1 bit per character. Shannon, 1950)
If you want to do multiple searches *and* you know the search string contains more information than the word size of your computer (8 English characters per byte, and note “convict” is only 7), hashing can optimize searches because each hash can represent multiple characters simultaneously and you can keep the hash around for subsequent searches.
The optimal hash length is then 3.59 characters (round to 4) per hash to optimize average hit rate, or 2.71 characters (round to 3) to optimize worst-case hit rate (“Most efficient chunk size”, Durlam, 1972). Having chosen which you want to optimize, you make a table of hashes, then “hashes of hashes”, and then “hashes of hashes of hashes” up to the size of the file, which results in an optimal evenly-spaced branching tree of hashes. The tree is small relative to the original file (adds 25% to the original size) and will give you optimally fast checking for strings.
To search for “convict” for example, calculate the possible hashes that could identify it: “CONV”, “ONVI”, “NVIC”, and “VICT”. Check each hash in the file for one of these, get 6,000 hits and then check those positions individually. This is roughly as efficient as simple text searching for small words (such as “convict”), about length of the original text (3.3 million checks), due to the shortness of this particular string and the low informational content of English.
Despite the poor performance of the example cited, hashes of hashes quickly wins out when searching for longer strings.
But for simple text searching, done once, it’s hard to beat the naive algorithm.
As a followup to the above:
The rsync command wants to optimize not just file comparison, but file transfer. Since the files may be on different computers, the actual *transfer* of information is the bottleneck. Hashing is so fast it can be done at close to the RAM access speed.
Consider updating a 10GB file on 2 systems, with an rsync process running on each. This 10GB file might be a virtual machine that you want to save, or the zipped contents of your video blog.
Suppose your virtual machine has several updates, so a small number of files got changed. Or maybe you added another video to your collection, changing only the last section of the blog zip file.
Video case: Comparing the overall hash shows that the zip files are different; however, the 2nd level hash (4 of them, 25% of the original file each) might show that 3 out of 4 of the original hashes are the same, so that only the last 25% of the file needs to be copied across. You can then recursively check the last 25% and see that half of that slice is unchanged, then recurse into those changed slices, and so on.
At some point the hashes refer to memory chunks smaller than the buffer transfer size, and the size of the hash table you’re checking gets bigger than the buffer transfer size, so at some point there’s a tradeoff and you just start copying file data.
VM case: Comparing the overall hash shows lots of changes at the high resolution end, but when you get down to a 10MB granularity you find mostly matches, with a few changes. There will be about 2N mismatches for each single file change (each file probably crosses a hash boundary, so changes 2 hashes). If each single file is less than 10MB in size, that’s 2N*10MB changes per file. If the upgrade changed 40 applications, and each app upgrade touched 3 files, that’s 120*2*10MB => 2.4GB of copy to update the 10GB file.
Note that for the VM example the 10MB level of hashes contains 1024 entries, which is a trivial amount of information relative to the 75% savings you get for making the effort.
This is a significant amount of savings when used on a, for example, 50MBit wifi speed.
And to be completely clever, you can consider *all* your data as one continuous bit string and calculate the hash table for everything you want to update, in order, rather than individual files. (Managing missing files as a separate step.)
The optimal hash tree can result in massive savings in copy time.
rsync CRCs and string searching hashes are two very different operations that both use an algorithm called a “hash function”, but that’s where the similarity ends. The reason a hash is useful in data transfers is that it can be quickly computed on a block by block basis; any delta between both ends means the block is corrupt, and needs to be retransmitted. The only property the hash needs is to detect substituted or transposed values so the data can be resent. You can select the block size based on the reliability of the data link; let’s say a noisy RF link might have a data corruption every few seconds, so you might want to keep the block sizes small to minimize the amount of data retransmitted. Or if you’re on a reliable fiber connection, you might increase the block sizes to take advantage of the medium. Some protocols even dynamically adjust the size of the blocks based on the amount of CRC errors on the link.
For searching, a hash algorithm makes for a highly efficient dictionary index. You index the keys with a hash as they’re being inserted, and keep the hashes in a sorted structure (b-tree or whatever). Then when you have a lookup in a million entry table, you compute the hash on the search term and find it in your data structure. A b-tree will get you the match in about 13 integer comparisons. This produces brilliant performance when you’re building a huge database.
Note that these two operations benefit from completely different types of hash algorithms. A communications line benefits from speedy and simple computations on ultra-low-end hardware that doesn’t have space to keep a lot of state (typically they can be kept in one register), they use small blocks of varying sizes, and so a CRC algorithm is usually preferred. (There’s a reason CRC algorithms are classified as “checksums” rather than “hashes”.) But CRC16 is subject to lots of collisions, and would be a poor choice for a dictionary index. There you’ll want a fast hash algorithm that’s tuned to your architecture size and is optimized to quickly produce largely different values of output for very similar inputs, such as an FNV hash or Jenkins hash (this is referred to as the avalanche effect). These take bigger algorithms and are less concerned with internal state.
And neither of these classes of hashes are designed with the security needed for cryptographic work. For those you need a specialized cryptographic hash, such as SHA or BLAKE. A cryptographic hash specifically needs to be irreversible (by studying the hash value it is not possible to determine any of the input bits) and it has to have collision resistance (given the original data, it is not possible to find another string that produces the same hash value.) But crypto hash algorithms are a lot more heavyweight than CRCs or regular hashes, so they’re not good for those applications.
I’m still stuck on the Euler thing. It seems to work for summation of all folded sums. Try 10: 10+1, 9+2, .. 6+5 are all 11, so there are 5 pairs resulting in a sum of 55. That works well for every even number of sums, but what about odd summations, say 9? 9+1, 8+2, .. 6+4 ??? What about the left over 5? Well 5 +5 is 10, but that’s unnecessary. Just add the four sums of 10 and 5 to get 45. That works for all sums of odd numbers. Hmm? What’s the sum of 1..8: 8+1 + 7+2 + 6+3 + 5+4 = 36. Sum of 1..7: 7+1 + 6+2 + 5+3 + 4 = 28. Do these constitute a series? .. 28, 45, 55, .. 5050 .. ?
Imagine a big blank square.
Place “1” in the top left corner, then place “1 1” (which is 2) underneath that, then “1 1 1” (ie – 3) underneath that, and continue all the way to the bottom, where you place 100 of the ones, left to right, as the bottom row.
At a glance, you have half the square filled with 1’s in a big right triangle, top (single 1) to bottom (one hundred 1’s).
You want to tally all the “1”s in the box.
The area of the box is the side squared, so 100^2 => 10,000, but you’ve only filled half the box so the total number of 1s is half that, or 5000.
Now you have to deal with the odd-even case. When the number of rows is odd, each row in the top half matches a row in the bottom half, except the one in the middle. So 99 matches with 1, 98 matches with 2, and so on down to 51 matching 49. The middle line is N/2 (50, in this case) isn’t matched so the result is N^2 – N/2: sum(1 .. 99) => 5000 – 50 => 4950.
Or another way to look at it is to note 1 .. 49 all have counterpoints that add to 100, then add the 50 in the middle: sum(1 .. 99) => 4900 + 50 => 4950.
In the even number of rows case is exactly the same, noting that 100 matches up with zero. So it’s the original sum, plus the extra 100 at the bottom. sum(1 .. 100) => sum(1 .. 99) + 100 => 4950 + 100 => 5050.
Or another way to look at that is that each item in the top half matches an item in the bottom half *including 100* matching zero, so you have 0 .. 49 cases of 100 (which is 50 cases of 100), plus the extra 50 in the middle. sum(1 .. 100) => 5000 + 50 => 5050.
The original formula N^2 – N/2 can be rearranged to be N(N+1)/2, which I believe is the formula you’re looking for, and works for odd and even sums.
If you are interested in such things checkout plocate and how it can get a 2500 x speedup on search times with an index file that is less than half the size of the index used by mlocate.
I learned that the ‘generic’ most efficient way for searching substring are ‘deterministic finite automate’. For sure, they are not the solution if you look for string1, then string2…. But if you are looking for any occurence of String1 and String2… at the same time, do not hesitate.
Most regular expressions ( regexp) can be translated in such an automate. The automate is such that you feed it with one character at at time, you use its transitions table and get new state. You read your file only once. Many regexp processors will code the automate from your regulat expression and compile it, and will execute it with almost no overhead.
It is also very very efficient if your pattern is somehow autosimilar (eg aabaaa) and in the worse case it is just like a basic algo. Unless you have a very specific use case such as rsync, it hard to beat
Especially do not search a known-before- starting set of string with another method
I remember from my algorithms course that you can make string search functions more efficient by doing some analysis on the target string first, looking for self-similarities.
For instance, if you have a target like “foobarfoo”, and you compare and find a partial match of up to 6 letters (but it fails on the next comparison), then rather than moving just 1 character forward in the search text, you can move forward by the length of the partial match. However, if you had an 7+ letter partial match, you can only skip forward to the point where the target string repeats itself (ie, 6 letters).
If partial matches are rare, then this doesn’t help much. But if they are common, it can help a lot.
You might be thinking of https://en.wikipedia.org/wiki/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm ?
That’s ‘included’ in the automate that is generated from a regexp, at least in serious implementation. This and the search for several string at the same time still mutualising the autosimilarities between the various string you are looking at.
I a convinced that except for some rare niche cases, looking for a set of one or more strings in a wide corpus is really best adressed by proper translation of regexp as a finite deterministic automate.
Once the regexp is compiled, you just have list of transitions, a list of final states and a ‘current state’. Almost nothing! It is really fast
Rk od easy to understand, show off with boyer moore
Could one read up to 8 bytes (depending on cpu arch and length of search string) at a time and xor with the search string as you slide down the text? That is do the comparison in bigger chunks.