If you’ve ever dealt with orbital mechanics or sophisticated computer graphics, you’ve probably run across the math term quaternions. [Anyleaf] has a guide to the practical use of this math concept which focuses more on practicality than theory. We like it!
Quaternions are one of at least two ways to model rotations in a 3D space. Most people are familiar with the classic Euler angles which cover yaw, pitch, and roll. However, this method is prone to some ambiguities — in other words, there are multiple ways to go from one Euler state to another and all are equally valid. In addition, Euler angles are prone to gimbal lock where two of the axes are parallel and, thus, don’t have a different effect on the object’s orientation. There are several ways to combat that including the use of quaternions.
If you think gimbal lock isn’t a problem, don’t forget that the Apollo IMU had this problem because they used three gimbals instead of four. The system would detect it was in gimbal lock and require manual intervention. This prompted [Mike Collins] to joke “How about sending me a fourth gimbal for Christmas?”
Of course, you can convert between Euler angles and quaternions subject to the ambiguity involved. The section about converting from quaternions is marked as future work, though, so you might need some more resources to fill in that blank. If you want more detail in general, [Anyleaf] suggests an excellent page from [3Blue1Brown] and [Ben Eater] that has explorable videos (the title graphic comes from one of these videos) and also a PDF tutorial from the Weizmann Institute of Science.
Honestly, we know not everyone likes math and it is true that — especially today — you can do a lot without diving into math. But if you do know the math behind things it often makes things easier or, sometimes, even possible. It is like assembly language. You probably don’t need to know it these days, but if you do know it, helps sometimes in strange and unexpected ways. So why not brush up on calculus or advanced topics like the Laplace transform?















What I’d like to know is there some experiment to determine the mass of these things?
You may be thinking of quarks, not quaternions.
Complex numbers are 2D vectors based on the sqrt of -1.
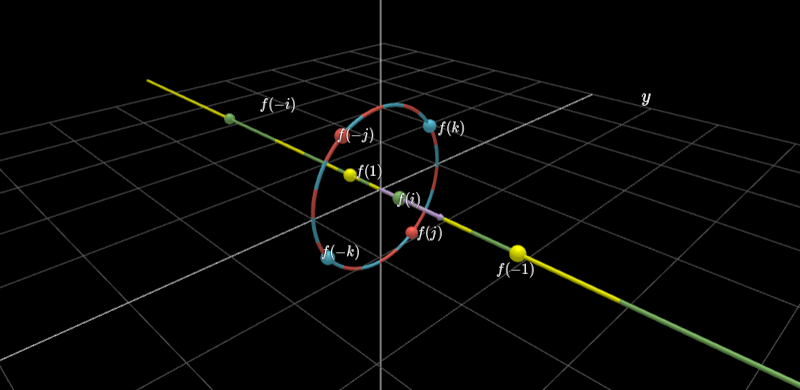
Quaternions attempts to extend complex numbers to 3D space. This can’t be done in 3D, but it works when you get to 4D space: you define 4 roots of -1 i,j,k such that i*i = -1, j*j = -1, k*k = -1, and i*j*k = -1.
This gives you 4D vectors (a + b*i + c*j + d*k) which act in 4D analogously to the way complex numbers act in 2D space.
I’ve often wondered if quantum physics could be simplified by using quaternions instead of the Dirac matrices. That might give a more intuitive geometric understanding of the relationships instead of just “use these matrices to get the result you want”.
Try this https://www.youtube.com/watch?v=ltvCOrIWcEY
For those who do not want to open links blindly to find out if it is interesting:
“Biquaternions and the Clifford algebra CL(2) (Video 4/14).”
A harsh jump into the great topic of Geometric/Clifford Algebra.
There are some links below that make it much easier to understand why Quaternions are hard to understand while Geometric Algebra makes it easy and at the same time reveals the secrets to easily understand Quaternions.
“you define 4 roots of -1 i,j,k”
‘Splain that to me Lucy.
1) i*i = -1, 2) j*j = -1, 3) k*k = -1, and 4) i*j*k = -1
But more importantly, i * i = -1; j * j = -1; i * j != -1.
Those aren’t roots. Those are relations between the imaginary bases. The roots of -1 are i,j,k. So there are only 3 roots of -1, and then a real basis.
That’s just a mathematical magical spell to allow unicorns in a lower dimensional world. It’s used to fit a 4 dimension vector space in a 3 dimension world. It’s impossible, but if you accept that it is, it works beautifully and that’s what we care about.
Now see? That’s all they had to say.
I think you mean 3 roots of -1. The three imaginary units, like you say, are i,j,k and then the fourth basis is real, not imaginary.
And to your question about quantum physics, yes you can forgo gamma matrices and use quaternions, but it’s not necessarily a simplification, nor is it inherently an actual explanation of anything physical in terms of geometry and such. Remember, the gamma matrices are designed to be a Clifford algebra, which is a generalization of various algebras where the four dimensional version is isomorphic to the quaternions, but the algebraic relations when you start getting to spinors and quaternions are remarkably abstract, and I’m nowhere near qualified enough to explain them simply, if I even fully follow the relations in the first place.
But it’s always important to remember mathematical models, even if accurate, do not inherently correspond to an actual explanation of the thing in question, which is why when it comes to something as unintuitive as quantum physics, it’s probably better to work with the model that is the simplest to get the results you want instead of chasing your tail of an aesthetic you prefer, trying to give it more meaning than it likely has. It’s not like the Dirac matrices come out of nowhere, so investigating their origins would be just a useful.
Actually, it is 1+3-dimensional. The a component is a scalar, the b,c,d components are bivectors (rotation elements in the three coordinate system planes)
If you just look at the coefficients it may look like a 4 component vector, but that way you loose the important structure that helps you to understand the underlying mechanism.
The misterious product result of -1 means that Quaternions “anticommute”, that is you can flip the position of the elements, but then the sign flips (“commute” means you can flip without any effects).
Everything folds in quite nicely if you look at it from the perspective of Geometric/Clifford Algebra. You will find that Quaternions can be extended easily into Multivectors, useful for rotation, translation, reflection, scaling etc., and if you just want to have rotation, only the “Quaternion” components are non-zero. Makes a lot of sense then.
Best introduction is “The vector algebra war: a historical perspective” by James M. Chappell et al. https://doi.org/10.1109/ACCESS.2016.2538262
Regarding Quantum Physics and Dirac matrices:
Yes! There is!
It’s called Space-Time Algebra, and the trick is to take a 3D Geometric algebra and cleverly extend it with a time component. This give you a rich structure that just describes Space-Time, and you can simply translate Dirac matrices into that, but it’s much easier to handle (and understand.)
Read all about it, starting with
Space-Time Algebra by David Hestenes, Birkhäuser 2015, ISBN 978-3-319-18412-8
I think today you will find the Clifford Algebras in any sophisticated graphic system. Clifford Algebra is quite amazing and quaternions are a special case. Maybe the extension called Geometric Calculus are what is used most. For the last 15 or 20 years I have been telling students going into engineering and physics that it might be worth their while to have a go at Clifford’s work as presented by and expanded by these guys (I just checked Amazon and the number of books and the fields they are used in has exploded.) https://www.amazon.com/Linear-Geometric-Algebra-Alan-Macdonald/dp/1453854932 https://www.amazon.com/Geometric-Algebra-Physicists-Chris-Doran/dp/0521715954/ref=sr_1_3 and there is a 2 hour lecture by Lasenbey here https://www.youtube.com/watch?v=m7v2IUJtC3g
Do I have to go back to watching PBS? I apparently missed the “Clifford the Big Red Algebra Dog” series.
Do watch the 3Blue1Brown / Ben Eater videos linked in the articles. It’s really not that important to understand how it works (unless you are a mathematician, in which case you already understand) – what’s important is that if you have a need to do 3D rotations, the videos show what variables you adjust to have specific effects on the orientation of your models. If you’ve used applications that let you drag a point on a 3D object to rotate that object, then you have seen quaternions in action. I will probably use this in the future. And I am not a mathematician, but I do use matrix transforms to rotate things in three dimensions, and qaternions can be converted to such matrices.
No no no no no. Stop poking sharp things into my brain.
It is too busy visually (structurally) and with too many colors (that don’t contrast enough). It really increases complexity instead of reducing it. I am not a fan of 3blue1brown videos for that reason.
Don’t give so many visualizations, make a very simple one to drive the point home. It’s nice you can rotate all and move “sliders”, but things like colors or hiding details is not available.
Though the effort is clearly amazing, the educational effect is limited.
I like ben eaters presentation with his bread board computer a lot more.
You’re talking about a four dimensional number system that is not commutative that possesses three imaginary bases. They are not structurally simple, and 3blue1brown’s job is not to simplify something to the point of it being an improper conceptualization of the thing in question. He does a very good job of demonstrating what they are, and the interactive portions do a good job of demonstrating small, digestible components of them, and some of their use cases. The mathematical things you can say about them get far, far more complicated.
It’s complicated because it’s incomplete, and all the weird behaviour comes without reason and explanation.
Geometric/Clifford Algebra explains Quaternions just fine. No need to imagine a 4th dimension where there is none.
None of that makes any sense. Quaternions are not “incomplete” and are isomorphic to the four dimensional Clifford Algebra Cl0,2(R), where with the Clifford Algebra, the bases are 1, e1, e2, e1e2 that anti-commute, where everything except the 1 squares to negative -1. Quaternions are literally just a different formulation of a specific Clifford Algebra, but again, are isomorphic to it.
Saying there is no fourth dimension with respect to quaternions is misunderstanding the mathematics, one thinks. There are four orthogonal bases for quaternions, hence it’s a four dimensional number system, so I’m not really sure what you’re going on about, just as the case of the Clifford Algebra that represents them is four dimensional.
And the Clifford Algebra in question is just as complicated as Quaternions are. The “weird” behavior is the same between both sets, and Clifford Algebras get even more “weird” when you look at them over a complex vector space. Thinking these are simple concepts that will be simply visualized is… not reflective of the actual mathematics involved.
After thinking on this, I believe you’re crossing streams a bit in your comment, and I think I understand where you’re coming from. The Clifford Algebra required for working in 3 dimensional space is NOT the Clifford Algebra that’s isomorphic to the Quaternions, and my previous comment to you was on the basis of the Clifford Algebra that IS isomorphic to the Quaternions. The Quaternions are four dimensional, and there’s a four dimensional Clifford Algebra isomorphic to them, but for the problem at hand, that Clifford Algebra isn’t needed.
If the problem in question is dealing with rotations in 3 dimensional space, then yes, you can do that with a different Clifford Algebra that does not represent the Quaternions but is easier to understand. There are quirks with the Quaternions that make certain operations dealing with 3D space be less simple than a Clifford Algebra dealing with 3D space.
But that doesn’t inherently mean they’re more ideal, and this is where my knowledge is completely lacking. Working with a Clifford Algebra for 3D space is easy to reason about, but that doesn’t inherently mean it’s best to program with. Clifford Algebras can be utilized to reduce computational complexity of problems, such as finding Hamilton cycles, but how they compare computationally to quaternions for 3D rotations isn’t clear to me. Quaternions are often used in computer graphics because of both issues with Euler angles (like gimbal lock) AND the computational complexity difference. Quaternions are just more efficient to compute. The question I can’t find an answer to is how the computational complexity compares to Clifford Algebras. Because in the context of this discussion, how well YOU can understand it is less important than how well a computer can compute it.
If you have information on computational complexity comparisons, I’d love to read through it. I briefly looked but couldn’t find much.
There is an actual practical guide to quaternions, but I can’t seem to find it in all my bookmarks.
It gave you rules of thumbs to guess the rough rotation from quaternion values, and how to combine them and in which order. The actual nitty gritty of math is not that relevant, especially not as something to learn first.
And if you’re a real masochist, you should check out dual quaternions right after reading the linked article.
Would that be the same thing as “octonions”?
Semions?
(fnarr)
Octonions are a thing. Not a thing, as you might surmise from the name, made of eight onions, either.
8 onions. Seems a bit much for any recipe.
I think Outback has just such a dish.
No masochism or mystification here:
GAME2020 0. Steven De Keninck. Dual Quaternions Demystified https://www.youtube.com/watch?v=ichOiuBoBoQ
Quaternions are just a stupid way to do 1 thing of the many things geometric algebra can do. Nothing against your post but we should stop teaching eachother the wrong stuff.
Quaternions are a simple, clean, and effective approach to a whole host of rotation problems in video games (to say nothing of space navigation). While you may find scrawling it out on a bar napkin is a brain burster, using the built in quaternion math functions to “subtract one rotation from another” without having to unwind eulers, avoid gimbal lock, or bloat up your code with world/local space matrix transformations… quaternions are the right stuff.
In short: Read the great, fun to read and revealing
“The vector algebra war: a historical perspective” by James M. Chappell et al.
https://doi.org/10.1109/ACCESS.2016.2538262
While Quaternions solve the problem just fine, but they are really hard to understand because they only show one dimension (actually, blade) of the whole picture. The result is that people are struggling to understand, following recipies without understanding, and cannot abstract the system to create more powerful stuff because they are tangled in the mind-bogging un-obviousnes of Quaternions. It’s like looking at a 3D object by taking 1D and 2D cross sections.
With Geometric Algebra you will find that scalars, vectors, bivectors and so on are forming a perfectly sensible system, and Quaternions are just the bivectors in the 3D Geometric Algebra. The same is true for Complex Numbers and 2D Geometric Algebra
What I did not know and you probably as well is, that the Vector and Quaternion concepts where in rivalry already more than hundred years ago, and the unifying concept of Geometric/Clifford Algebra was known at that time, but just not as popular. More on that in the document cited above
Do you have a comparison of the computational complexity involved between the two? Just because geometric algebra can do many things does not mean those methods are what you actually want to compute the problem with. Calling it “wrong stuff” while simply calling quaternions stupid is a poor argument that you should feel bad about, and ignores the reason quaternions are used: efficiency.
Then there’s this ..
https://www.quantamagazine.org/the-strange-numbers-that-birthed-modern-algebra-20180906/
I only knew Ben Eater as the guy who made breadboard 8bit computers popular. Didn’t know he also did work on educational applets. The guy’s a wizard.
I see THAT word, and this comes to mind;
https://en.m.wikipedia.org/wiki/Allan_Quatermain
B^)
“Marty ! … You’re not thinking 4th dimensionally!…. Yeah I have a problem with that.” – BTTF
Then there’s this: https://marctenbosch.com/quaternions/
Thanks. I will look into rotors before working on any more 3D applications. I’m serious.
ive been walking on 4d spheres for some time now.
@Al Williams:
I encourage hackaday to tell more about Geometric Algebra, which is so much more understandable and powerful than Quaternions!
Hackaday already had an article regarding Geometric Algbra in 2020-10-06:
GETTING STARTED WITH GEOMETRIC ALGEBRA FOR ROBOTICS, COMPUTER VISION AND MORE by Maya Posch.
https://hackaday.com/2020/10/06/getting-started-with-geometric-algebra-for-robotics-computer-vision-and-more/
The CG people are using Geometric Algebra highly successful (ever heard of Chris Doran’s Geomerics and their Enlighten package to provide Radiosity, which was highly sought for and finally acquired by ARM. Worth a story!).
Electric/electronic people can use the structure to better understand and handle the Maxwell Equation (sic! It is one thing still written too complicated):
Geometric Algebra for Electrical and Electronic Engineers by James M. Chappell et al. 2014
https://doi.org/10.1109/JPROC.2014.2339299
Physicists use it for Space-Time Algebra, making a lot of topics from mechanics to quantum physics easier to understand and to handle.
“TODAY’S THE DAY YOU FINALLY LEARN QUATERNIONS”
I read the article, and still don’t understand. Maybe tomorrow.
Sorry, the article was posted on 2022-09-05, you missed it by two days.
Perhaps in the next 128 years, another opportune date will occur.
Just came here to say,
“TODAY’S THE DAY YOU FINALLY LEARN QUATERNIONS”
Nope.
No it’s not.