[Rolinychupetin] insists that his recent video is not a lecture but actually a “recitation” about Bode plots. That may be, but it is still worth a watch if you want to learn more about the topic. You can see the video below.
If you haven’t run into Bode plots before, they are simple plots of magnitude or phase vs. frequency, usually plotted on a log scale. Named after Bell Lab’s [Hendrik Wade Bode], they are useful for understanding filters or anything with a frequency response.
Of particular interest are the zeros and poles of the graph. Simplistically, you can think of these as the dips and peaks of the response curve. The math is a bit more complicated than that, but you can learn more in the video.
Of course, these days, we are more likely to see a Bode plot from a simulation tool or test instrument than plot them by hand, but it is good to understand what’s going on. As you might expect, if you can generate a frequency sweep, it isn’t that hard to display a Bode plot on an oscilloscope. Or just use a network analyzer.

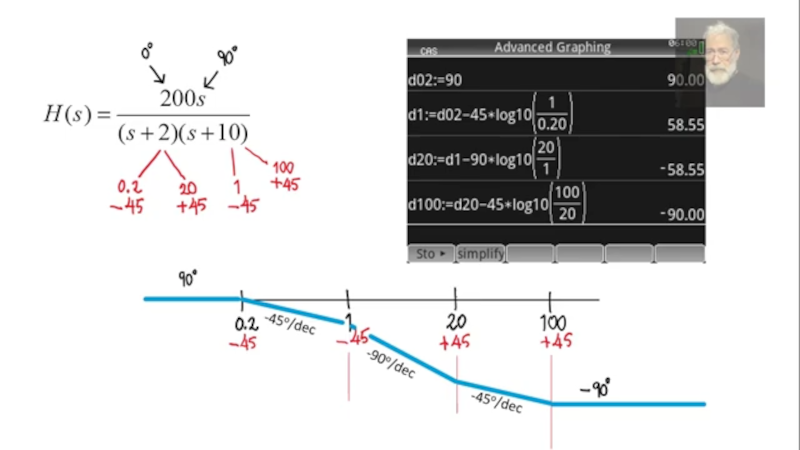













This “45 degrees per decade” is just wrong. Phase is not ‘degrees per decade’, it’s just degrees.
What he’s referring to is the slope of the phase plot with respect to the (log, hence decade) omega axis. The ultimate phase is in degrees, but as you are moving from left to right along the omega axis, it’s helpful to think of the phase as increasing with a slope.
Hey this is my professor! He’s an excellent teacher, and his videos are really useful when reviewing for exams! He teaches the fundamental circuit analysis courses as well as electric machines (the one I’m taking right now).
I have made it through 40 years of engineering only to realise I have been pronouncing Bode incorrectly- I pronounced the plot name as Bode as in “mode” . Next I’ll find out I should be pronouncing Moog as “M-ohh-g” and not “Muu g”.