The languages we speak influence the way that we see the world, in ways most of us may never recognize. For example, researchers report seeing higher savings rates among people whose native language has limited capacity for a future tense, and one Aboriginal Australian language requires precise knowledge of cardinal directions in order to speak at all. And one Alaskan Inuit language called Iñupiaq is using its inherent visual nature to reshape the way children learn and use mathematics, among other things.
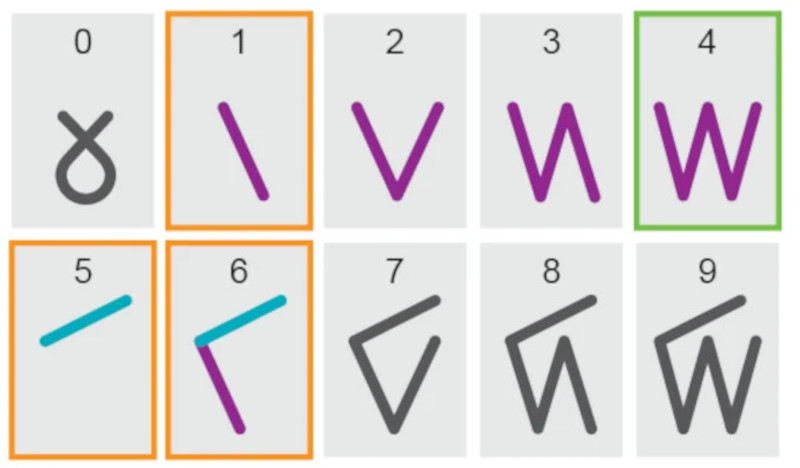
Arabic numerals are widespread and near universal in the modern world, but except perhaps for the number “1”, are simply symbols representing ideas. They require users to understand these quantities before being able to engage with the underlying mathematical structure of this base-10 system. But not only are there other bases, but other ways of writing numbers. In the case of the Iñupiaq language, which is a base-20 system, the characters for the numbers are expressed in a way in which information about the numbers themselves can be extracted from their visual representation.
This leads to some surprising consequences, largely that certain operations like addition and subtraction and even long division can be strikingly easy to do since the visual nature of the characters makes it obvious what each answer should be. Often the operations can be seen as being done to the characters themselves, instead of in the Arabic system where the idea of each number must be known before it can be manipulated in this way.
This project was originally started as a way to make sure that the Iñupiaq language and culture wasn’t completely lost after centuries of efforts to eradicate it and other native North American cultures. But now it may eventually get its own set of Unicode characters, meaning that it could easily be printed in textbooks and used in computer programming, opening up a lot of doors not only for native speakers of the language but for those looking to utilize its unique characteristics to help students understand mathematics rather than just learn it.
















Interesting. Biquinary. I wonder if it is borrowed from the abacus, or sprung up independently.
I think both come from people often having two hands with five fingers.
Fingers and toes?
Fingermath.
https://en.wikipedia.org/wiki/Chisanbop
Yes, the students who developed this language in the 1990s were indeed aware of the abacus. And then they developed a base-20 one. https://en.wikipedia.org/wiki/Kaktovik_numerals#Abacus
Iconary?
Yeah yeah nah, otherwise we’d all be working in binary notation. This is just another linguistic curiosity that will go nowhere and eventually be completely forgotten as far as everyday use is concerned, just like all of the languages from Australia, because the way of life that may make them relevant is no longer practiced by anyone.
“because the way of life that may make them relevant is no longer practiced by anyone” – this is precisely what the end of the article explains isn’t the case…
Except that it _is_ the case in Australia. Homogenization of cultures that interact is to be expected and there is nothing wrong with the process. This is the price of all of the other benefits of globalisation and the internet. You are more likely to hear young aboriginal Australians playing rap music from NYC rather than anything from their culture from >200 years ago. That is their free choice and I support it because it is very offensive to treat people as if there were a quaint museum exhibit and place limiting expectations on them.
Pessimisim here from someone who always uses a username with unspeakable symbols in unicode is indeed ironic
Touché !
Fortunately for humanity it is the worst unspeakable thing I have ever done.
Chinese and Japanese people also have it much easier with math thanks to their number system. For example, in Japanese instead of “thirteen” they say “juu san” (ten three) and for “one hundred and thirteen” they’ll say “hyaku juu san” (hundred ten three). All you need to know are numbers between 0 and 10, 100, 1000, 10000, and you easily know all numbers in between. French is probably the worst when it comes to numbers. Something like “eighty four” ends up “quatre vingt quatre” (four twenty four), but then “ninety four” is “quatre vingt quatre orze” (four tenty four orze) haha what the hell is an orze?.. i know i know, it’s actually (four twenty fourtneen) but it’s still stupid. Yay for languages which simply math.
That’s easier *talking about* math. They pretty much exclusively use Arabic numbers when *doing* math.
And then there’s French numbers…
99 – quatre-vingt-dix-neuf (literally “four twenties plus ten plus nine”)
And then there is Danish:
trehalvfems -> tre-(halv-fem)-s -> three and (halv-five)[twentie]s -> 3+4.5×20 -> 93
QUATorze
japanese kanji don’t translate to computers well though, with hundreds or thousands? of different characters and combinations thereof. the 26 + 10 alphabet and decimal system can be supported on a keyboard. maybe it doesn’t matter because technology has developed so that kanji could be entered on a drawing tablet, but in the past the roman alphabet was a massive advantage in computing.
For Japanese, most people don’t use any kind of drawing tablet, but input characters in one of two ways using a keyboard:
1. Direct kana input. Often used in phones (f e. By me!), It by older people on computers. For example つなみ is the key presses.
2. Romaji input. You type in Roman transliterations like “tsunami”, and it shows up as kana like “つなみ”. It takes more keypresses, but has the advantage of using they same qwerty layout as is typically used for English.
Either way, this is possible because there aren’t that many kana. In order to get to kanji, the computer will show a list of possible candidates sorted by likelyhood. Generally you press space to cycle through them and press enter to select one. So after typing in つなみ, I might select the first entry, 津波. It’s similar to using predictive text entry in English, actually.
Quatorze is 14
And 94 could be either “quatre vingt quatorze” or “Nonante quatre” depending on the speaker region.
And 14 is quatorze, not quatre orze
Exactly!
That x20x system comes from the Celtic languages I believe, I think Irish Gaelic does the same thing.
Is easy necessarily proper?
Neat. Like Roman Numerals but a lot smarter. I don’t know about so many strokes compared to Arabic, but you write fewer characters.
This reminds me of something… was it.. maybe the Romans? Nah, they didn’t have a zero.
Except the Romans did the whole subtraction thing that makes it more complicated.
Bold title.
4 paragraphs dont deliver on it though.
Just one comment: the written numbers have less than 20 years now (they were created in 1994), it is the use of them orally that is ancestral. Interestingly, Canada has considered use them (I don’t know where in the process if the idea they are at the moment).
It might be easier to integrate into Inuit Syllabics, are the Iñupiaq going to adopt syllabics?
Finger Abacus based symbols?
Vigesimal ?
https://en.wikipedia.org/wiki/Vigesimal#Use
example; French umbering is 20 based, 80 being quatre-vingt, aka “four twenties”….
And others
Isn’t this basically tick marks? |||| with a slash though them for five?
Yep. Tally marks.
“The Kaktovik numerals started as a class project to adapt the counting system to a written form. The numerals, based on tally marks, “look like” the Iñupiaq words they represent.”
I *highly* doubt these people aren’t also going to be taught 0-9, because cheap calculators and phone keyboards, aka the main way people interact with math, use it.
Maybe it’s just as valuable as the times tables or all the other random math stuff nobody uses that we learn to theoretically help us learn other math, so that a few percent can get a job that actually uses it while everyone else just has a better appreciation of how to use a calculator.
The few percent that actually use math are the only ones that matter.
The rest are just freeloading on the work of the few.
They are the only ones whose *minds* matter. Their bodies, as self-healing reproducing “robots” with some cheap integrated processing, are still relevant until we have von Neumann replicators or advanced synthetic biology to create physical workers another way.
Did chatgpt just get out again and now posting on hackaday?
Surprisingly many of the numeric systems around the world trace their origins to India and the middle East of 8000 years ago. I personally like how the Sumerian numeric systems prevail until this very day (base 60) in things like the number of minutes in an hour, and the number of degrees in a circle. Numbers don’t lie, and they indicate that there’s a lot to our pre-history that we just haven’t connected yet.
“Numbers don’t lie”
Err… nope. “Lies, damned lies, and statistics”.
The UK census has just “shown” that 1/67 Muslims are trans, and those for whom English is not their first language are 5x more likely to be trans than native speakers. Quite clearly these numbers lie, and almost certainly relate to a badly worded question on the census.
“Numbers don’t lie” does not mean “every statement expressed with numbers is true”.
“Numbers don’t lie’ is both true and a lie.
The numbers don’t lie, being numbers. But the person saying ‘numbers don’t lie’ is almost always a liar that’s trying to get his numbers/lies accepted without questioning.
Put in a similar way:
Figures don’t lie, but liars sure do figure.
>Bartley reports that after a year of the students working fluently in both systems, scores on standardized math exams jumped from below the 20th percentile to “significantly above” the national average.
I’m afraid they’ve fallen into a trap. The article desicribes how the system was developed by the students themselves, and then taught alongside arabic numerals, which means the students actually got twice the math training because they were doing the work in double.
Naturally, if you train harder, your scores will improve faster. Whether that makes you any better at math is debatable.
Did they get twice the amount of training though? If the way human beings learn is primarily through repetition then “twice the training” would indicate “twice the hours”. If they only had the same number of hours (not double) then they didn’t have “twice the training” and thus the differentiating factors are the content of what was learned and how they learned it.
Possibly not twice, but still they went through a lot more trouble to incorporate the new system as opposed to just learning the old. More time spent on the subject, while approaching it through more varied examples, usually leads to greater learning outcomes.
Plus, there’s the Hawthorne effect where the test subjects become more engaged in the topic while they’re being tested, which leads to improvements in performance. When the new system becomes routine, performance drops to previous levels or lower, because the real effect was masked by the greater motivation of the test subjects. Everyone can perform at 110% for some time, but eventually fatigue will set in.
“More time spent on the subject” – again, if it was the same number of hours, that wasn’t “more time”. Remains to be confirmed whether they had the same number of hours, or more.
Everything is relative; even if the effect you describe did happen, it would be in a system where people have still learned to understand Mathematics better through the language used so the general ability in Maths should be improved when compared to the previous system.
True, but the point is that the results can be explained by other means than by the special base 20 number and symbol system being used.
Learning these kinds of arbitrary patterns can be entirely superfluous, and if the method of teaching is not motivating in the first place it can even become counter-productive with worse learning outcomes; exactly like “new math” where you were actually spending most of your effort learning set theory instead of basic arithmetic.
Or, another example, in most language studies, the teacher is attempting to teach from the same point of view as they were taught as language teachers. As a result the students are forced to learn concepts and rules – essentially a whole different meta-language that analyzes and describes languages – rather than simply learning to speak in a different language. They have to learn what a concept like “accusative” means before they can follow the teacher’s instructions and answer their questions, which is simply more work and extra cognitive load. Nobody thinks in these terms when they’re actually conversing in a language.
In the same sense, it’s not efficient to teach multiple number notation systems for basic arithmetic. You can get the point across using any one of them, and the question is about keeping the kids interested enough to assimilate the information.
>whether they had the same number of hours, or more.
Or completed more work in the same number of hours, or more homework, or spent more time on the subject outside of class voluntarily etc.
Usually in a math class, most kids are just trying to avoid work and entertain themselves to make the time pass quickly. Simply engaging them in the work improves results tremendously.
The only way to get to 110% is 25% Mon-Thu and 10% on Fri.
The very expression is just dumbass football coach talk.
It takes Zen like focus to get anywhere near 100% for a moment, 110% is just dumb.
The first time I hear some dumbass in a business environment say ‘give 110%’ I’m updating my resume. It’s a tell. GTFO ASAP. That moron can’t be helped.
And it’s not the hours of training really. If you repeat 1 + 1 for two hours, you’re not going to learn it any better – or at least you’ll have diminishing returns. Long term retention requires you to space it apart and “sleep over it”.
Repetition leads to boredom, which shifts the brain into “I’ve seen this before” mode and it stops memorizing stuff, but if you pose the same problem from a novel angle, such as learning a different notation for the same thing, the brain goes “Hey, this is new, better pay attention.” and you get a dopamine hit, and your brain makes a note to remember it better.
But that’s still repetition, just from a different angle. If you learn a list of vocabulary the night before a test and get a full score, it’s very easy to forget some of them within a week (perhaps a day, even) if you don’t repeat those words in different contexts.
Yes, but it is from a different angle which avoids the boredom response.
The most effective form of repetition learning is by introducing the same subject as part of different problems, where the subject acts as a necessary stepping stone to solve the question. The problems themselves can be quite trivial, and should be so. Of course if you simply phrase the question differently like “Johnny has five apples…”, it’s not novel – it’s just convoluted.
What “rote learning” usually means is saturation learning, where you repeat repeat repeat until you can reproduce the correct answer by reflex. I say A, you reply B. That kind of learning is what’s mostly employed in elementary level math classes where you’re filling in sheets and sheets of “5 + _ = 8” type of problems where you simply fill in the correct answer. That’s exceedingly boring and very inefficient.
If you set the students to design their own system of notation, and rules for using it, then automatically you set up a situation where they have to learn the matter that you’re teaching as an instrument for achieving their goal. To think about the matter, they have to think in terms of the fundamental arithmetic, which means they repeat it over and over and automatically memorize it.
https://www.gse.harvard.edu/news/ed/17/01/bored-out-their-minds
“A 2014 study that followed 424 students at the University of Munich over the course of an academic year found a cycle in which boredom bore lower test results, which bore higher levels of boredom, which bore still lower test results. Boredom accounts for nearly a third of variation in student achievement.”
I’d like to see a proper system of notation for ternary ie (on), (off) and (both on and off) and get rid of binary in computers. Maybe it exists already?
Or quarternary, including “neither on, nor off” – a Schrödinger’s Cat-based, quantum system 😜
Yep, even better !!!
I put your comment into Bard and it came up with this: ‘This system is called Schrödinger’s Cat notation. It is a base-4 number system, which means that it uses four symbols to represent numbers. The symbols are 0, 1, 1/2, and -1/2.’ Using ‘1/2’ is confusing and inappropriate IMO.
BTW i then asked Bard: ‘is there such a system as Schrödinger’s Cat notation?’ and they replied ‘no there is not’. So obviously Bard spontaneously invented it and then, only minutes later, forgot about it again.
I see what Bard did there 😝 Although it really ought to have replied:
There is
There isn’t
There is and isn’t
…
I’ll show myself out
Sorry, I forgot the:
There neither is nor isn’t
🤦🏼♂️
A brief DDG search indicates it might possibly be referred to as “Bra-Ket” notation?
IIRC, Scottish courts can declare Guilty, Not Guilty, and “we can’t prove it, but we think you did it”
AKA “not proven”, which is particularly poignant in cases of state-fabricated and sponsored charges involving a witch hunt and where their must-be-protected-at-all-costs witnesses perjure themselves…
It’s been invented already, and the values are known as “true”, “false”, and “file not found”.
The obvious answer why 60 is the number of minutes per hour is because it has maximal number of dividers up to it’s double, which just makes it convenient and obvious choice. There is nothing magical about it. The same reason goes why people used to count stuff in dozens instead of multiples of ten, e.g. you can divide dozen eggs between three people without a quarrel.
Huh. A more socialist counting system?
A more mother at dinner time counting system. :p
I agree with others here. This is just a bad idea. Unlike language, arabic numerals are near universal which means no matter where anyone is in the world they can write them down and everyone understands. THIS IS AMAZING. Even if by some miracle this was a better system to represent numbers (I’m sure 444 looks awesome using this system), it is not so much better as to cripple children into not learning a universal notation. If a system can make 0.1% more students comprehend math at the cost that all students in that group can not share math with others this is a net negative. If we are teaching students both systems why not just spend 2x as long teaching them the one everyone else uses I’m sure that will have better results.
I’m for octal or hexadecimal combined with scientific notation. Fewer digits to write/type.
Oops, make that just hexadecimal with scientific notation.
an interesting system from my state. i think we may have had an assignment on these, but im not sure. i graduated back in 2000 and the system seems to have originated a few years before then. they seem familiar. of course this would have been more taught in village schools, where i went to school in anchorage, so i don’t think it would have been any more than a social studies assignment.
anyway go read the article to see the full matrix. i like that the number system forms its own look up table. such that the ones and fives components define the whole set.
“centuries of efforts to eradicate it and other native North American cultures” [citation needed]
Try the Encyclopedia Britannica entry on eugenics.
It’s horrific.
Sorry, “Encyclopaedia”
My great, great, great grandmother’s language has 150 fluent speakers. The few words I know have been dropped into otherwise English text, where I wonder and look them up.
I’ve been working on a similar “visual” numeral system for base-16. This system gives some great insight into some useful features that I should build into my system. Thanks for the write up!
Somewhere back in 4th grade or so I started to make pencil dots on the numbers 1 through 9 like domino dots and then count them and on the next digit and have the answer. The shapes of the numbers mostly convey this already. I still do 60 years later if not empowered with some common tech. Multiplication tables, gak! I forgot about that mental torture from back then, perfection expected from my brain of what could be printed on a business card.
Ten years or so ago I heard they found a subset of dyslexia that is distinctly mathematical. I was elated! A few years later I’m browsing a 1930’s Popular Science and see an article with this same discovery and it had a fancy name. They covered it up and kept pushing a subject on a disabled group of students. This must be recognized.
We were going to the moon then I knew then things would be different in the very near future.
Now with AI math can go figure itself out. We’ll have all the answers.
The interesting thing about this to me is that the number system works almost identically to the Mayan number system, although the symbols are different (but have a similar orthography). I wonder if this was the result of communication between the various indigenous societies of the Americas, or if both cultures came up with the base-20 numeric systems independently.
Get ready for a teacher rant…apologies in advance, but how many times do we have to go down this thoroughly flawed path before WE learn that it’s a fools errand?
We already adopted this frankly idiotic idea that children are failing at math because they don’t understand what they’re learning. So, we upended the way we’ve taught math for generations and reorganized it around nonsense marketing terms like, “number intuition” and an endless parade of others. What was the result? Children did even worse. Why? Well one interpretation was that we took away their in-house tutors. It seems another is that they don’t understand what they’re learning…again. Oh know…let’s go consult someone who’s never taught kids and play boggle with the standards again. You know, maybe the problem is that they don’t understand the symbols for numbers…let’s just make that kid learn them twice. He/she totally won’t end up illiterate to numerals and unable to pay for things, right guys? Right?
The reality is that the last paragraphs tell you every thing you need to know about the problem, it’s ready to be put into brand new textbooks. This is yet another hill that Big Ed and their marketing department is willing to sacrifice our kids on. How about we focus on something useful, like open-source textbooks? Or actually offering courses on tutoring to ill-prepared parents? Something without a perverse profit motive centered on our kids?
I came across your article on the Native Alaskan language reshaping mathematics, and it’s truly remarkable. The way the Yupik language incorporates unique mathematical concepts and perspectives is both fascinating and inspiring. It’s a powerful testament to the interconnectedness of language, culture, and mathematics. Thank you for shedding light on this incredible linguistic influence and its impact on mathematics. Great read!