Cryptography ain’t easy. Seemingly small details like how many times a computationally intensive loop runs can give the game away. [Lord Feistel] gives us a demo of how this could work with nothing more than poorly designed code, a resistor, and an oscilloscope.
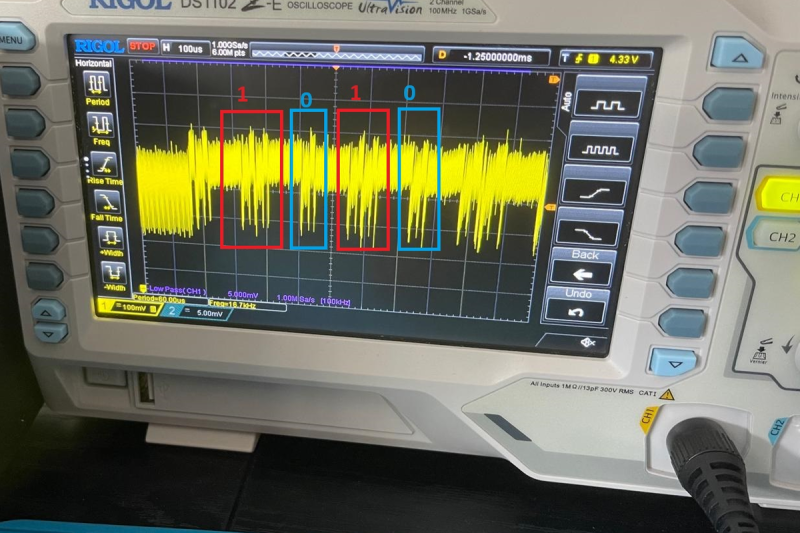
The hardware side is, as mentioned, really simple. Put a resistor inline with the Arduino and monitor the voltage drop across the resistor with the scope. When the chip is working hard, it consumes more current, and code sections that take longer will show up as longer dips.
On the software end, it’s only a little more complicated. The RSA encryption scheme involves a lot of exponentiation and modulo-taking. Here, [Lord Feistel] is targeting a naive way of computing the exponents quickly, and demonstrates how you can read the exponent straight out the chip’s power demand.
Implementing this attack against a real-world RSA algorithm, in the context of the Arduino doing other stuff, will be harder. And we don’t know if the algorithm implemented in “standard” Arduino libraries is smarter than this one. (If you know, let us know in the comments.) But still, this is a cool example of just how simple and straightforward it can be to eavesdrop on bad code.
If you only need to bypass encryption instead of breaking it, check out [Lord Feistel]’s other tutorial on power glitching that we featured previously. If you haven’t played around with the hardware side of security, it gets deep pretty quickly, but you can at least dip your toes in the shallow end with what you’ve got in your closet.















I suppose with Arduino encryption broken, soon we’ll finally be able to run custom code on them! :o)
+1
If you look closely at the output on the oscilloscope, you can actually see the decrypted text:
Eat more Ovaltine
+1 but Ovaltine’s a drink, although I’ll confess to eating the powder out of the tin more than once https://youtu.be/zdA__2tKoIU?si=aDkIwu3Czid2w6O_
Might want to add some water before you “eat” it.
You add water??
What a menace
I am wondering if the implementation of RSA was deliberately modified to show this weakness.
For people more interested in this, have a look at the ChipWhisperer. (No affilation, just a project I remember having seen long ago).
https://hackaday.com/blog/?s=chipwhisperer
Indeed easy to find ,but the tags are a bit of a mess. :)
It was definitely a simplified or naive version.
This is a known channel for cracking encryption.
Hello actually you are correct is a dummy implementation of Fast Exponentiation.
As you said it is a very well-known stuff, I made it just to prove a point and show people how the “Leak” happens.
Next chapter I will break real library.
Hello guys,
I am the Author.
This is just a PoC I just got some Fast Exponentiation from stack overflow to show.
This is a PoC of an SPA ( Simple Power analysis attack ). I made it more to prove a point.
Also, I think the main focus is to show the shunt stuff that almost every paper I read they don’t let clear how they are doing it.
However is valid to point that it is possible to do it in some official libraries and that will be my next post.
This begs the question: how can you implement fast exponentiation that doesn’t leak? I assuming if you make every functional call take the same amount of time and consume the same amount of power it won’t be fast anymore. There is too much data to fully store all possible values in a lookup table (but perhaps a hybrid method using a partial lookup table, might help?). I assume that using a RNG to generate random operations to the function call would confuse the attacker a little, but with enough data those would be averaged out.
You can keep fast exponentiation fast without making it data dependent. fast exponentiation has time complexity of log(N) to 2log(N) depending how many bits are one or zero. If you expand it to 2log(N) it’s still fast while being consistent. Even better to expand it to 3log(N) to keep power footprint consistent.
One could simply modulo the iteration count by a randomised number. If it’s even, pause execution by a randomised number effectively mitigateing the timing leak.
Adding random noise to a variable-time algorithm doesn’t really help – with enough data, you can cancel out the randomness. Making algorithms constant-time is necessary to prevent timing attacks.
And queue the satellite hackers rejoicing in 3….2….1!