Multiplication on a common microcontroller is easy. But division is much more difficult. Even with hardware assistance, a 32-bit division on a modern 64-bit x86 CPU can run between 9 and 15 cycles. Doing array processing with SIMD (single instruction multiple data) instructions like AVX or NEON often don’t offer division at all (although the RISC-V vector extensions do). However, many processors support floating point division. Does it make sense to use floating point division to replace simpler division? According to [Wojciech Mula] in a recent post, the answer is yes.
The plan is simple: cast the 8-bit numbers into 32-bit integers and then to floating point numbers. These can be divided in bulk via the SIMD instructions and then converted in reverse to the 8-bit result. You can find several code examples on GitHub.
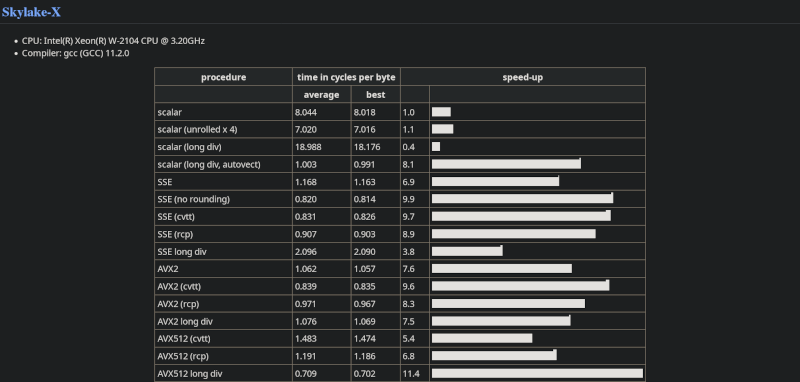
Since modern processors have several SIMD instructions, the post takes the time to benchmark many different variations of a program dividing in a loop. The basic program is the reference and, thus, has a “speed factor” of 1. Unrolling the loop, a common loop optimization technique, doesn’t help much and, on some CPUs, can make the loop slower.
Converting to floating point and using AVX2 sped the program up by a factor of 8X to 11X, depending on the CPU. Some of the processors supported AVX512, which also offered considerable speed-ups.
This is one of those examples of why profiling is so important. If you’d had asked us if converting integer division to floating point might make a program run faster, we’d have bet the answer was no, but we’d have been wrong.
As CPUs get more complex, optimizing gets a lot less intuitive. If you are interested in things like AVX-512, we’ve got you covered.















For 8 bit by 8 bit division without vector extensions, it might be fastest to look-up a reciprocal in a table and use multiplication. But vectorized versions will still be significantly faster.
Yep, I’ve done this on MSP430(f5529) because it has a multiplier FPU, but the FPU cannot do division.
WRT the fact that sometimes using FPUs are faster than doing integer math, that has been the case (in some circles) for 40 years.
And sometimes doing magic math is faster than either. ;)
https://en.m.wikipedia.org/wiki/Fast_inverse_square_root
Thanks for the rabbit-hole! Fun read…
I kinda doubt it. Definitely not for a single operation – the cache hit alone would kill you. But in order to get the right answer you can’t just do “value * reciprocal” because for any reasonable LUT you’d need to round to get the correct answer to avoid the precision loss in the reciprocal (and I’m not sure you can actually do it exactly without a LUT with precision bigger than 8 bits?). The fetch + mult is already costing you like 6 cycles in the best case with everything in cache. With multiple operations you might start to win.
There are times were contrary to the popular belief, use of LUTs can give surprising results, even when I am living with the idea that what I am doing right now must be horrible because it will trash the cache and make things even more slow. It might even make most people to not even consider it because it’s something from the 90s that is bad for current hardware. But that’s why it makes sense to sometimes test these assumptions. Unless of course once code is so horrible that even a LUT would make it faster, so nothing is absolute.
I could point examples from my experience. All of the examples are over iterrations over several pixels. One has to do with replacing a division with LUTs. In a modern CPU. But as we know integer divisions are still bad. The other was when I was making a big 128k table that takes two 8bit pixel values and gets 16bit pixel color. Something like a fake palette colormap in 16bpp. On a Pentium 1. One of the early CPUs where I first heard in Abrash’s books maybe, that things have change and making a LUT especially such a big, is a No No. Previously I would do integer shifts and ORs to create 16bpp RGB values the typical way one does it. It wasn’t as fast as I’d like on the Pentium. Then I decided to try this and I was in horror when I tried because I knew “it was considered horrible idea especially with a huge 128k LUT for the small cache of the Pentium”. And yet I went like double speed. I just stopped assuming any modern wisdom at that point and decided to try anything no matter how absurd and if it makes my code faster that’s fine. Sure, maybe I was doing something stupid in the original code but I am well versed in optimizing such things so relatively confident the non-LUT approach wasn’t that badly written to suffer more in performance than cache misses.
However, all ideas welcome. I was looking at a recent Casey Muratori’s video (with Primagen) where he infact replaced an integer modulo with floating point division and subtraction, with all the conversions from integer to float and then back, and made the compiler to do use the SIMD really well and get 4x speed. I’d also see that code before and be like “What? That’s gonna be way slower, what about the conversions?”.
https://arxiv.org/pdf/2207.08420
If speed is of utmost importance, why not just have a direct LUT for any slow operation taking two 8-bit operands? That’s a 64kB LUT. And the solution doesn’t need vector operations or have some minimum number of operations before breaking even.
LUT is usually 1 or 2 cycles per value on out-of-order architectures. The vectorized versions shown here get more than 4x speedup over that.
Could you explain this, as I don’t quite understand how that works.
If I need one instruction to perform that lookup-division, but the articles methid would be 4 times as fast, I’d end up with a quarter instruction?!
Vectorized instructions handle multiple values per cycle (SIMD, single instruction multiple data). AVX512 can handle 64x 8-bit values.
Right, but this all falls appart if you have 32bit ints (as wood a lut, or rather it be very expensive) or you cant parallize these divisions.
Anyway, subtle but understood. Thank you.
four results per cycle
IIRC vectorized means they run multiple divisions in parallel on the same core at the same time. So if you are doing more than one at a time then it will be faster.
“why not just have a direct LUT for any slow operation taking two 8-bit operands? That’s a 64kB LUT. ”
That’s a huge LUT. On a modern CPU you’d eventually evict the entire L1 cache doing that. And obviously embedding a LUT like that in the CPU is impractical, because it’s, uh, exactly the same as the L1 cache.
Embedded in the cpu, it would be in ROM, which is typically smaller than the RAM of the L1 cache. So not exactly the same. Nevertheless not a good idea, probably.
I was assuming the poster meant a programmable LUT, hence “any 8 x 8 function.”
Even for a fixed function LUT, though, for a math function a full LUT is a poor choice because there’s structure to the LUT, and it’s faster to use math since LUTs inevitably slow down as they get larger.
It’s funny because working with FPGAs you’d figure LUTs are a good choice for math in a lot of cases: only a single critical path. But I’ve ended up implementing so many of them as actual math after trying LUTs because the LUT is so big and the math can be trivialized and compacted.
If you really need the speed on an wide variety of processors write it multiple ways and test in a realistic manner at run time. Your be surprised how caused things are even within an architecture. (Examples, ftw, seti@home…)
I’ve been working hard as I can over the past 2 years to completely retrain my intuition about good code.
A cache miss is 200 cycles (for the sake of arguing) so it’s possibly 10-20 floating point divisions!
Data orientated design completely over turns just about everything I thought I knew about fast code.
This.
In my opinion it goes even further:
The data is the core and any program is just a replaceable convenience to handle the data. The language is not important, it just makes certain manipulations more convenient.
Probably would be much faster using a GPU
Most people have those installed
Or have integrated graphics on the cpu…
Algebra, trigonometry, and caculus is something GPU are extremely efficient compared to a cpu
Especially logarithmic operations and floating point math
Except that you’d have to wait for a round-trip on the bus to talk to the GPU. The APU should at least avoid that.
It all comes down to dataset size، If it’s big enough then then the latency doesn’t matter.
While I can and do use openCL, I never even look at SIMD intrinsics.
I write code that’s simple and clear enough that GCC can vectorise.
I can and do use OpenAC and OpenMP (in the past).
Once you take the perspective of the data flow (data orientated programming) you find that much of the micropotomization is a false economy.
The amazing work being showcased here is vital though and interesting. It’s not a criticism of that.
It’s just that no matter which route you take you better have the data laid out so it can be applied efficiently.
If the data was buried in large structs and in long arrays of that structs. No matter what you do you will have bad performance as you utterly thrash your cache.
You might think that’s contrived but it’s actually the most common data pattern in use by “career programmers” using OOP.
Interesting. Reading this I was curious if this would be applicable to the AMMX SIMD instruction set in the Apollo 68080 CPU core but it doesn’t support division so no. It does support XOR though so I wonder if this is workable using SIMD XOR division … 🤔