In the last edition of Don’t Fear the Filter, we built up two examples of the simplest and most-used active filter of all time: the two-pole Sallen-Key lowpass. This time, we’re going to put two of these basic filter blocks in a row, and end up with a much sharper lowpass filter as well as a bandpass filter. For the bandpass, we’ll need to build up a quick highpass filter as well. Bonus!

I claimed last time that the Sallen-Key lowpass would cover something like 80% of your filtering needs. (And 72.4% of all statistics are totally made up!) These two will probably get you through another 10% or so. Honestly, I’ve never built a standalone active highpass, for reasons we’ll see below, but the active bandpass filter that we’re building it for is a great tool to have in your belt, especially for anything audio.

Cascading Sallen-Key Lowpasses for More Rolloff

If, as we said last time, a two-pole filter has two reactive elements (the two capacitors) and a rolloff of -12 dB per octave, surely we could just add another copy of the same circuit downstream and get even more filtering done, right? Yes, but it’s not optimal.

A little bit on a detail that I glossed over last time. All filters of a given order have the same asymptotic (eventual) rolloff rate of -6 db per octave per pole. The main performance difference among the various responses — Butterworth, Bessel, or Chebyshev — is in how quickly the filter gets from flat in the passband to the eventual rolloff rate. A 1969 VW Bug will drive the speed limit at the same rate as a Lamborghini, but how fast you get up to the speed limit can differ.

It turns out that, as long as you’re stacking filters, you can pick one to be slightly peaky (resonant at the cutoff frequency) and the other to be a little too flat, and the combination will have a nice flat transition that nonetheless gets to the rolloff rate faster than simply stacking identical filters. Which is to say, the overall filter has a Butterworth response, but the individual stages won’t. This makes the design a tiny bit more critical, but it’s nothing you can’t handle.

Picking the optimal resonance values is a matter of math, and not really informative. In the old days, you’d look them up in a table in a book and then scale up the prototypical 1 Hz filter to your needs, using pencil and paper. Today, we cheese out and head to an online calculator. Click Butterworth, 4-pole, enter 1 for the various stage gains, and enter your cutoff frequency, and you’re done. This tool is even nice enough to draw the circuit diagram and pick the nearest capacitor values out of the standard-value E6 or E12 series. Bam!

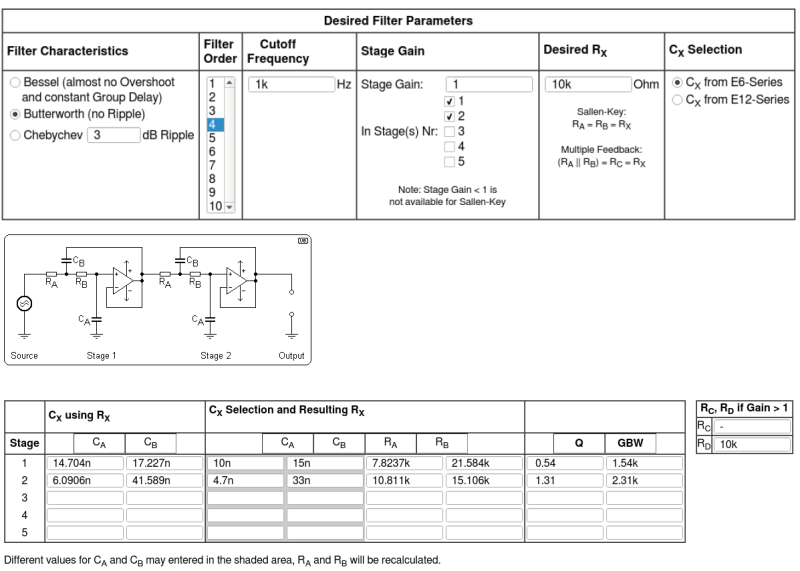You’ll notice that there are no round-number resistors anymore: the values are strange, and no longer in integer ratios. Getting close to these values is a good goal, but again with a Butterworth response, nothing is too critical. So where it calls for a 21,584 Ω resistor, I’d just pull out a 22 kΩ out of the box. With the particular tool above, you can even measure the actual capacitors that you’re using, enter the real values into the spreadsheet, and it will re-calculate the resistors for you. A nice touch, but not necessary with a forgiving circuit.

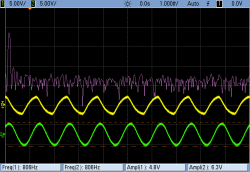
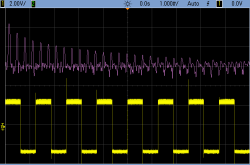
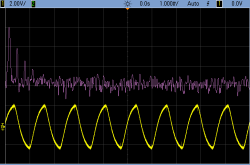
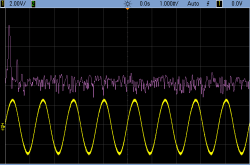
Constructing a fourth-order filter is slightly more than twice as much work as a second-order filter, but the results are worth it when you need them. Here are some FFT spectrograms to show off. In both cases, the input is a square wave at 800 Hz. Square waves have harmonics of diminishing volume at all of the odd values, so there’s a substantial peak here at 2400 Hz and another at 4000 Hz.

In all of these scope shots, the input is a square wave at 800 Hz being run through a filter with a cutoff at 1000 Hz. The first pane displays a comparison of two- and four-pole filters. The remaining three scope shots also show the Fourier transform of the source and two filtered waves. You can see how the peaks fall off nearly twice as fast in the four-pole filter. Success!

The Sky is the Limit?

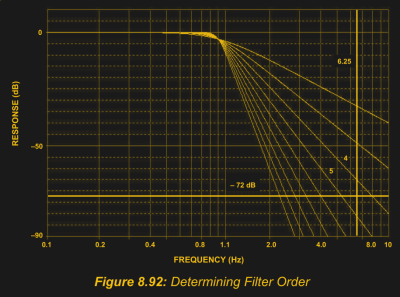But why stop at four poles? Each additional pole-pair only costs you two resistors, two capacitors, and an op-amp stage, right? To maintain the overall non-resonance of the filter, the different stages will need carefully controlled resonance values, and this will mean exact capacitor ratios. With practical parts tolerances, this gets more and more difficult. Additionally, as more stages get added on, the resonance that the final stage requires to compensate for the early stages puts increasing demands on the op-amp’s frequency abilities, in particular requiring a higher gain-bandwidth product.

Finally, at some point the simplicity advantages of the relatively slow Butterworth response is outweighed by the extra stages, and you’re better off designing a lower-order Chebyshev filter than a higher-order Butterworth. On the other hand, the four-pole Butterworth is a beautiful and stable filter. Don’t overcomplicate things unless you really need to.

Two-Stage Bandpass Filter

And now for something completely similar: cascading highpass and lowpass filters to make a bandpass filter. If a lowpass filter knocks out the high frequencies and lets the lows pass, you won’t be surprised that a highpass knocks out the lows, and a bandpass knocks out both the highs and lows, leaving the juicy middle frequencies intact. The strategy is to take the signal first through a highpass followed by a lowpass.

Bandpass filters like this are a great frontend to any ADC scheme where you have a general idea in what range the frequencies of interest lie, but you don’t want to narrow down on one thin slice of the spectrum. If you’re lowpass sampling with an ADC, you’ll at least need the lowpass filter. If you’re not interested in the lowest of the low frequencies, why not trim them off in analog while you’re at it?

For instance, in a capacitive-sensing application, a person touching a metal plate is an event that can span frequencies from something like 10 Hz up to maybe 1 Hz — even a short tap will last 100 ms, and you probably don’t care if the person holds their finger on the button for much longer than a second. Here, bandpassing the signal has the effect of throwing away the low-frequency environmental changes (humidity, temperature) that will cause capacitive drift over the course of a day, and also throws away high-frequency noise like interference from nearby electronic devices. Doing this up front in analog makes the programming and analysis work in firmware very easy.

The Highpass

There’s not much to say about the Sallen-Key highpass filter, because it’s the same circuit as the lowpass with the capacitors and resistors swapped. In the lowpass we set the resistors equal and the capacitors in a ratio of 1:2, but now the capacitors are equal and the resistors are 1:2 for the Butterworth response. If you’re powering the op-amp off of a single-sided power supply, as opposed to matching positive and negative voltages, you will need to create a constant mid-rail voltage (GNDREF in the diagram). Doing so can be as easy as making a voltage divider out of two relatively low-value resistors. If you have an unused op-amp stage anywhere, you can buffer this “virtual ground” as well.

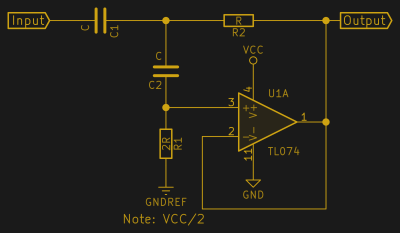Active highpasses just aren’t as useful as lowpasses. Highpass filters really shine in radio-frequency applications, but most op-amps are too slow to keep up. Still, you’ll find them in audio applications like crossover and equalization circuits. As with the lowpass, the highpass version of the Sallen-Key filter can be cascaded for steeper rolloff.

The one time I’ve built a standalone highpass was in a bat-detector preamp, filtering out the audible portion of the audio range to focus on the bats’ high-frequency chirps. If you’ve used active highpass filters, I’d love to hear about it in the comments. Am I missing obvious applications?

The Bandpass

The bandpass simply cascades a highpass and a lowpass. This circuit isn’t intended for extreme selectivity of a particular frequency, and a rule of thumb is to make the highpass and lowpass cutoff frequencies differ by at least a factor of five or so. This is a good fit for the human vocal range — 75 Hz to 1000 Hz fundamentals, with important content up to 3000 Hz — or for pre-filtering slow-moving DC analog values before sampling them with an ADC.

When you’re aiming for a particularly tight frequency band, this circuit may not help that much. Narrow bandpass filters are a separate topic of their own, and I’ll cover them along with narrow band-reject (notch) filters on their own, because they’re tricky to design right, but are very useful when you need them.

As mentioned while discussing the highpass filter, there is no need for an extra DC-blocking capacitor on the input of this circuit because the highpass already takes care of that. There’s also no need for DC-blocking between the stages, because even though the second stage is a lowpass, the signal has already been centered in the middle of the op-amp’s response range by the time it gets there. So the only difference between DC- and AC-coupled bandpasses of this design is the addition of an output capacitor.

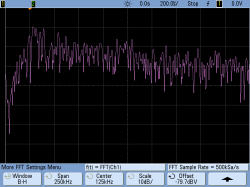
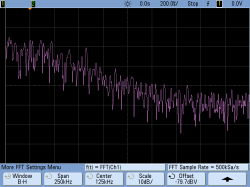
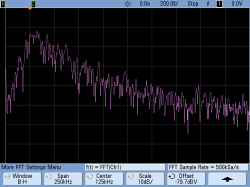
To demonstrate this circuit, I built up a highpass with a cutoff at 20 kHz and a lowpass with a cutoff at 50 kHz. Feeding white noise into this bandpass filter gives you a good feeling for the frequency response, at least as well as my ‘scope will capture it. You’ll note that the slopes of the highpass and lowpass sections don’t look the same. This is partly due to the fact that frequency rolloffs are multiplicative in nature — they would look the same on a log scale in frequency. Indeed, this would be the empirical version of a Bode plot.

Wrapup

The two-pole Sallen-Key filter that we built last time is a workhorse, but sometimes you need a racehorse and sometimes you need a show pony. Stacking two of the units that you already know together, while taking care to tweak the resonance values just right, makes the four-pole design easy to build and quite stable when you need that extra rolloff. Similarly, stacking a highpass and a lowpass together is child’s play and adds a new filter type to your toolkit.

And since all of these circuits are made with (multiples of) the same circuit topology, perhaps with the resistors and capacitors switched around, you could easily imagine making a single circuit board based on a two- or four-op-amp chip where you just plug in the right values for the passives, maybe with optional AC-decoupling stages, and you’re ready for anything. Since most op-amps share a common pinout, it would be easy to swap them out as well. Hmmm…maybe I’ll do that.  If you beat me to it, post up in the comments.

Up next are going to be the single-purpose filters: tight bandpass and notch filters. These are useful when you want to emphasize or reject a tiny sliver of the frequency spectrum while leaving the rest ideally unchanged. Want to detect a particular tone or remove that nasty AC hum? Stay tuned.