How can you generate random bits? Some people think it’s not easy, others will tell you that it’s pretty damn hard, and then there are those who wonder if it is possible at all. Of course, it is easy to create a very long pseudorandom sequence in software, but even the best PRNG (Pseudorandom Number Generator) needs a good random seed, as we don’t want to get the same sequence each time we switch on the unit, do we? That’s why we need a TRNG (True Random Number Generator), but that requires special hardware.
Some high-end microprocessors are equipped with an internal hardware TRNG, but it is, unfortunately, not true for most low-cost microcontrollers. There are a couple of tricks hackers use to compensate. They usually start the internal free running counter and fetch its contents when some external event occurs (user presses a button, or so). This works, but not without disadvantages. First, there is the danger of “locking” those two events, as a timer period may be some derivative of input scan routine timing. Second, the free running time (between switching on and the moment the unit requests a random number) is often too short, resulting in the seed being too close to the sequence start, and thus predictable. In some cases even, there is no external input before the unit needs a random seed!
Despite what has already been discussed, microcontrollers do have a source of true randomness inside them. While it might not be good enough for crypto applications, it still generates high enough entropy for amusement games, simulations, art gadgets, etc.
Uninitialized RAM
Hackers often make use of hardware resources beyond their initial means. Here we will use volatile RAM, not as a memory unit, but as a source of entropy.
When power is applied to the MCU, its internal volatile RAM has unknown contents. Each flip-flop will be preset to a 0 or 1 state – a consequence of the imperfection of internal circuits, power supply glitches, surrounding current flow, or thermal (or even quantum) noise. That’s why the content of RAM is different each time it is powered on.
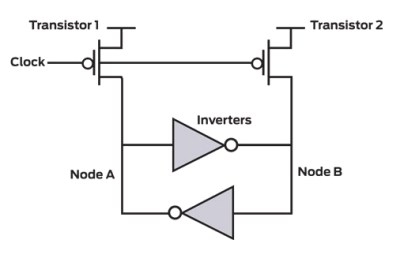A few years ago, Intel came up with a new way of generating true random bits, using a tuned flip-flop which was forced to a metastable state, and then released to a stable 0 or 1 state at 3 MHz rate. They announced that it will be embedded in a new generation of processors.
We don’t have tuned flip-flops in the MCU, but we have a lot of flip-flops and we can expect some of them to act as tuned. How many flip-flops do we really need to create a good random number using volatile RAM content? It surely depends on MCU RAM performance, so we should go through with some experiments to see how many bits are unpredictable after powering on the MCU. This instability occurs only in flip-flops which are highly symmetric, with well balanced transistors. We need those unpredictable bits to harvest entropy, so we should use as much data as we have – the whole data memory, before it is initialized to some known values. We don’t have control lines which could force RAM flip-flops to a metastable state, so we can use it only once – after powering on, and before initializing RAM.
Experiments
Let’s see the contents of a typical uninitialized MCU RAM. The following picture represents an initial state of one part (20480 bits) of data memory in PIC18F2525 MCU. There are 256 bits (32 bytes) in each row. The ones are red, and the zeros are yellow.
Obviously, there are less 1’s than 0’s in this MCU RAM, but it doesn’t really matter. There are two other matters of interest here: first, will this pattern be different if we use other MCUs (even from the same production line), and how many bits will be changed after the next power on, with the same MCU?
You probably guessed the answer to the first question – yes, each MCU has a completely different initial RAM pattern. The second question is more important, and the answer is that not many bits are different (unpredictable) after every power on. Yet there are enough to generate several random bytes.
Here is an experimental result of switching off and on PIC18F2525 twice. Gray pixels are both times read as 1’s, white are both 0’s, red ones are “0, then 1” and blue ones are “1, then 0”.
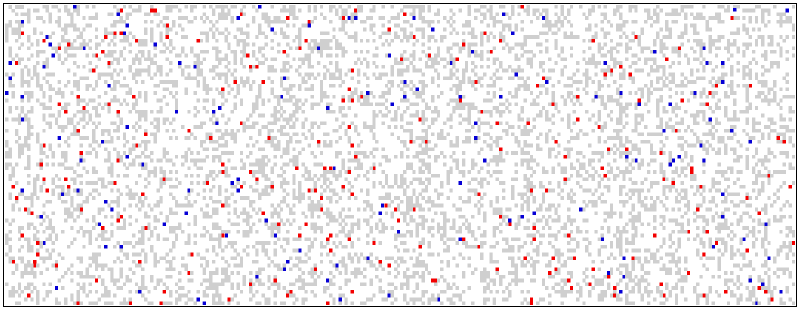
After some experimenting, you could see that generally the same bits in one MCU are unpredictable after switching on. They came from “good” flip-flops and they represent our source of entropy. I tested Microchip’s PIC18 and PIC24E MCUs only (the results are listed below), but any other MCU should act in a similar fashion. Examples shown here are generated with short Vdd rise time (high slew rate), as the on-off switch was between DC supply and the MCU. If you switch the primary side of the power supply which has a low slew rate, you will notice some patterns in memory contents, but somehow the number of unstable bits will actually increase.
Software
So, if you need a few random bytes (for PRNG seed or some magic number), you can use uninitialized RAM contents to generate them. You have to create a special routine, which will XOR (or ADD MOD 256) every byte in some block of uninitialized RAM to generate the first random byte, then the next block for the next byte, and so on. For instance, if your MCU contains 4K of RAM (like PIC18F2525, if you include SFR area), and you need a 32-bit seed, you can split RAM into four 1024-byte blocks and use them to generate four random bytes. Even if small parts of some blocks are already initialized (SFRs or variables for a routine loop), it should not affect the global entropy significantly. I used this technique about a decade ago for LED curtains, which simulated a waterfall in a casino. I built a lot of single chip MCU controllers for that project, and each of them was dimming 256 addressable LEDs. The trick with RAM random seed and 32-bit PRNG created beautiful chaos with a minimum of hardware.
You can also add more scrambling later, for instance you can call your PRNG routine from an existing timing loop (instead of NOP looping), so it will be invoked, supposedly, a random number of times until your program asks for PRNG output. This principle would not create a good random number sequence if used alone, but it can not cause the TRNG performance degradation, as the entropy can only grow.
The major limitation of this approach is that it can’t be used if there is battery backup, or if SLEEP mode is used instead of the ON-OFF switch. However, for some less sensitive applications (like digital arts or amusement games), you still have the long PRNG sequence to cover the period until battery replacement and a new Reset, when the seed will be randomized. You can also let the peripheral counter run in sleep mode and use it later in PRNG seed scrambling, supposing that the extra current in sleep mode does not affect battery life significantly.
We have to keep in mind that RAM contents must be uninitialized and used as-is, immediately after power up. It is also recommended to avoid high capacity Vdd decoupling, as CMOS RAM retention voltage can be pretty low. The worst case scenario is if you switch off the unit for a very short period of time, so that the voltage at the decoupling capacitors drops enough to activate Brown-Out Reset, but not to scramble the RAM contents. Luckily, it is very unlikely that the contents of RAM will ever be exactly the same, as there is always some “housekeeping” part of RAM (or at least MCU registers) which will be affected by program flow. Additional safety can be achieved by a multi-byte freerunning binary counter in RAM, even if the program doesn’t need it and never reads its state.
There are a few design approaches which you can use to enhance the quality of random numbers harvested from the volatile RAM. Never initialize the whole RAM with zeros or any other content, but only the necessary portion. If you don’t use sleep mode (but switch Vdd off instead), then don’t use too high decoupling capacity, or at least use an extra resistor in parallel with MCU supply. It will increase the supply current, but not by too much. Even 5% of total MCU supply current through this resistor will be enough to prevent voltage locking, when Vdd drops so that Idd is close to zero, or even when some external component sources current to the MCU (a beautiful example is described in The Mystery Of Zombie Ram article) . This resistor guarantees that RAM will not remember anything from its previous “reincarnations”, even if MCU was in sleep mode before switching power off.
Searching the Web for similar ideas and experiences, I stumbled upon a discussion with the topic Why don’t we use CPU/RAM-usage for “true” random generation. The author of the idea was heavily criticized, mostly because he suggested using initialized RAM for crypto applications. I also found the patent US5214423, which is based on a similar idea (used to reduce the possibility of repeated bus access collisions). Such patent applications scare every design engineer, as it makes the design process look like walking through a mine field – you never know when you might get sued for your ideas. The good news is that the legal status of this patent is “expired due to failure to pay maintenance fee”, so, hopefully, I have nothing to worry about – at least this time.
Experimental Units
The first experimental results encouraged me to build some units which use uninitialized RAM contents to create permanent random data stream. So I named the described idea (using uninitialized RAM contents for seed creation) “zero concept”, and then built three units to test three new concepts.
- Two PIC18F2525s with 8-bit one-way parallel communication, supported by simple handshaking. Slave MCU generates 16 random bytes, each of them based on 248 bytes of uninitialized internal Data RAM. Master MCU (shown in the middle above) receives those bytes and sends them to a desktop PC through the RS232 port. After receiving a 16-byte string, master CPU uses the PNP transistor to power off the slave MCU for 200 ms, which will supposedly create new random contents of RAM (according to my experiments, the “Zombie Ram” effect in 8-bit PIC MCUs takes place if the unit was switched off for less than 85 ms). Then the whole process is repeated 625,000 times, for a total of 10 MB of binary data, needed for randomness tests. It takes about 50 hours (the average rate is 56 bytes/sec).
- For the second test the same master MCU is used, but this time the slave is a 16-bit MCU 24EP512GP202. All MCUs are on the same proto board (that’s why they are on the same schematic diagram), and the program in the master MCU decides which slave MCU will be used. The left one is significantly faster (70 MIPS vs. 4 MIPS) and has much more internal Data RAM (48 K instead of 4 K bytes). One string of random data contains 192 bytes, so the 10 Mbyte file was created in 5.5 hours.
- And finally, only one MCU is used (24EP256GP710A) with 4 Mbytes of external SRAM (CY62177EV30). I had hardware leftovers from some old project, otherwise I would have used the low cost I2C SRAM and a small MCU. SRAM is powered off-on, and then read in a similar manner. The only advantage is high amount of RAM which resulted in high speed, so it took only 19 minutes for a 10 Mbyte file. It could be much faster, but the RS232 port is too slow to keep up with the fast random data stream creation.
Randomness Tests
Two batteries of tests were used, Diehard and ENT. The first concept (with two 18F2525s) had an excellent result – all 15 Diehard and 6 ENT tests passed! The remaining two concepts passed all Diehard tests, but failed one ENT test, which is the most sensitive indicator of randomness, roughly defined as “rate at which Chi square distribution would be randomly exceeded”. The required rate is between 10% and 90% (ideally 50%), but most TRNGs and PRNGs fall flat on this test, showing less than 0.01% or more than 99.99%. Fourmilab published an example of a well rated commercial TRNG which uses radioactive decay events – the ENT page linked above puts that hardware at 40.98%.
I am not a mathematician, but during the experiments I had a feeling that passing all Diehard tests should be quite easy (I don’t know why design engineers are afraid of it), as well as getting good values on almost all of the ENT tests – but this one is a nightmare! It fluctuates significantly during file growth, and tends to stabilize as the file becomes quite large, but even with 10 Mbyte files it is still not stable enough. This test is so sensitive that it is extremely hard to get values which are not saturated below 0.01% or above 99.99%, so even if it fluctuates somewhere between, it’s good news.
The first test run for my first concept gave a surprisingly good rating of 47.47%! The other two concepts failed (<0.01%), but I still had a secret weapon, called whitening transformation. Every hardware TRNG has some kind of a randomness extractor (mainly implemented in software), to minimize the bias and enhance the uniformity of data distribution. The simplest way to do this is to merge somehow (e.g. XOR) raw random data from the hardware TRNG with a software PRNG. So I added a simple 32-bit linear congruential PRNG routine to the MCU firmware (for concepts 2 and 3 only) – even though it might not seem like the best of ideas, it got the job done, as all results were perfectly in range. Here are ENT test results:
| Entropy source |
1. (8-bit MCU raw data) |
2. (16-bit MCU with PRNG support) |
3. (ext RAM with PRNG support) |
| Entropy (bits/byte) |
7.999982 |
7.999982 |
7.999982 |
| Compression reduced the size by |
0% |
0% |
0% |
| Chi square distribution randomly would be exceeded at |
47.47% |
34.29% |
42.24% |
| Arithmetic mean value (127.5 = random) |
127.4936 |
127.5478 |
127.4937 |
| Error for Monte Carlo Pi value |
0.03 |
0.05 |
0.00 |
| Serial correlation coefficient (0.0 = uncorrelated) |
0.000206 |
0.000434 |
0.000104 |
Diehard test results require much more presentation room, you can find them at www.voja.rs/rndtests.htm, together with binary files which are generated in this experiment and all source files in PIC’s assembly language.
Conclusion
At the end, all tested projects passed all Diehard and ENT tests. Even the commercial TRNGs (including the very expensive models) sometimes fail tests, and those $10 DIY units passed all of them!
It is important to keep in mind that this principle is based on undocumented characteristics of microcontrollers, and that it is impossible to reach the degree of safety required for crypto-grade applications. So, what about our high score? Well, at the very least, we proved that the uninitialized RAM can offer high quality random numbers, and that we can use it for seed generation in a lot of MCU applications. It’s simple, it’s free, it takes no extra room on the PCB and it consumes no extra current.
For those that want a random seed without building their own hardware, check out [Elliot’s] article on the NIST Randomness Beacon.
[Illustration by Bob Zivkovic]
Voja Antonic works as a freelance microcontroller engineer in Belgrade. His first microprocessor projects, based on Z80, date back to 1977, just a few years after the appearance of the first Intel’s 4004. He assembled the firmware manually, by pen and paper. In 1983, he published his original DIY microcomputer project called Galaksija, which was built by around 8000 enthusiasts in the former Yugoslavia. To date he has published more than 50 projects, mostly based on microcontrollers, and released all of them in the public domain.
So will this be used for the HaD votes raffle? :)
Great read btw, love the whole ordeal of randoms virtually never beeing random, has always intrigued me.
Yes, the one from the illustration :)
Speaking of which, I love the cartoons you’ve included in the gallery of your last two posts.
Who drew those?
It’s my friend Bob Zivkovic, there’s a link at the bottom of the article.
You can also pick the poster-size illustration here (8.8MB JPG): http://www.voja.rs/trng.jpg
Just to mention it, but in the votes raffle, if a non-registered (or whatever the condition is) person is the winner, then they don’t get the prize, so nobody gets the prize. Wouldn’t it be sensible, in that case, to just draw again?
As an incentive to join whatever it is, actually giving the prizes away, rather than keeping them and “Yah boo sucks! You lose!”, would work better. People respond better to carrots than sticks. Especially if the losing winner ends up with nothing less than they started with.
They don’t care at all to give the prize to someone , actually they have the greatest chances of never giving away anything when the requirements are you needed to vote. As I wrote in another post, when I was told that they had tried “REAL HARD” to give away the 1000$ (I was pointed to a video where they tried once, that person didn’t vote, they kept the prize..)
So , trying to give it away ONCE is trying super super hard? Tell me you couldn’t of wasted 10 more minutes to actually find someone who participated? And what about the people (like me) that cannot enter the contest because of local laws and rules? I can’t participate , so I just won’t vote, because even I did , I couldn’t claim the prize. So my .io user is just not involved at all in your gimmick of a contest, why was it part of the draw? How many other 1000s of accounts are just fake/empty/unused/last year’s contests/etc that just should not be part of your draw? How about you tell us exactly how many people had voted during your event? I’m guessing maybe 1000? 2000? ok let’s make it big , 10 000 users out of 76 095 , That’s 13.14% of the users who could really win the prize. which leaves 66 095 chances of nobody getting the 1000$ prize. And out of those , how many like me that could have voted , but couldn’t claim the prize?
Really? If that’s trying hard, I wouldn’t want to see you guys not giving a f*** about something.
Stop yer whining, if local law prohibits you to enter the contest, why even bitch about it?
And (though im in part to blame for the derail) this is a article about getting (actual) random numbers, not about the HaD Prize, if you must complain, find the proper article (any HaD Prize article) to do so.
Thanks.
Interesting approach. Rather than dividing memory into blocks and computing one random byte from each block, however, it probably makes more sense to use a mixing function such as a hash algorithm to mix in the randomness from the entire memory. That way, if the truly random bits are concentrated in one part of memory, you don’t end up with some seed bytes that are ‘more random’ than others. The really simple way to do this would be to simply hash the entire memory space and use the result as your seed.
You are right, the memory response is surely location dependent, as there were some visible patterns when I tried it with slow Vdd rise. Source addressing with some PRNG with mod(mem_size) would probably be helpful.
What would be interesting would be to record the value of each bit of memory over multiple resets as a stream, then apply the same randomness tests to them. How many bits pass diehard on their own?
Diehard requires 80,000,000 bits, and you need about 200 ms for each restart. So it would take about 185 days (half a year) to get the answer to your question :)
Yes, you need a lot of time to generate die hard data stream and even more for diehard. I have in fact been running a test data collection on one method (timer entropy) for close to two years and still don’t have enough for dieharder tests.
That said your approach hasn’t passed ‘diehard’ tests., Your PRNG has, which is a very different thing.
Some of the ram chips I knew back in the day did powerup initialization. alternated pages between 0x00 and 0xFF
“Why is my random number always 7?”
https://xkcd.com/221/
http://etoan.com/random-number-generation/index.html
No, it’s nine. http://img51.imageshack.us/img51/2848/dilberttourofaccounting.png
The ones I tested didn’t initialize, but most bits drifted towards some address bit, say A9 => as you say even pages of 0x200 bytes were mostly 0, odd pages were mostly 1.
Low-level startup code (typically included with a compiler/IDE processor package) does that sometimes as well.
“The major limitation of this approach is that it can’t be used if there is battery backup”
Not a problem. Just store the state of the random number generator in the battery backed-up RAM.
Exactly this is a problem. Saving the seed on a battery backed-up RAM achieves the exact opposite of what the author intended.
The idea is to force a shutdown and power up every now and them. If you shutdown your MCU a lot, the random seed will change a lot. If you have a battery backup, the seed will not change.
The seed changes every time you obtain a random number. As long as you have enough bits, the millionth random number will be as good as the first.
This is just saving a state in between power downs, like hibernating. Won’t affect the outcome negatively.
magic ball says
“try again”
You would probably get better randomness if you based the bits you choose off of some larger number of cycles. After all, a truly random bit state will only switch between two power cycles half the time — so about half the bits that happened to remain the same are probably properly random. (As someone else mentioned, the bits that toggled may not actually be random either — they may toggle predictably.) In other words, it should be easy to get several times more entropy out of this just by choosing bits based on four power cycles instead of two.
Most devices don’t have any control over the power cycling, though.
So choose one that does or cycle the power for it. Mosfets and transistors, how do they even work?!
The point of this project is to get some free random data after power up. If you need more random data, adding complicated circuitry (not just mosfets, but also a timer) for power cycling is stupid. You’d just use zener noise or timing jitter, or something else that’s easy to obtain and gives better results anyway.
Where did you get that idea from? This already requires two power cycles to work. If you do that, and then hard-code the addresses of sufficiently random bits, then you might as well run it six or seven more times.
You don’t need to know the address of the sufficiently random bits. You just calculate a hash over the entire memory.
I always sample a few least-significant bits from an floating ADC input. That universal background noise should be pretty random, right?
Good enough for most purposes.
That’s what I did for my electronic dice project. Just reads the noise from a floating analog pin each time it calls the roll function and uses that for the seed. http://hackaday.com/2011/01/17/electronic-dice-has-option-for-20-or-100-sides/
Another (very simple) option would be to continue rolling the dice at high frequency, and show the current result when the user presses the button, basically using the time between button presses as a source of random number.
Wierdest thing: When I lived in the States, there was this 60Hz signal everywhere that I suspect is the NSA trying to influence my random number generation. Now that I live in Europe, it’s 50Hz, which is naturally because the NSA’s random-number-waves lose momentum over the ocean.
Putting the microcontroller in a tinfoil cage _didn’t_ help with the problem! What can I do?!!?!
(OK, seriously, the distribution of the random numbers you get will be heaviliy weighted to the top and the bottom of the sine-wave that powerline radiation puts onto your ADC, with comparatively few values in the middle. Try it and see.)
Thanks for the chuckle!
Oh crap! I was just in Canada and I picked up 60Hz noise in my equipment while I was there. Do you think the NSA followed me?
No, that’s probably just insecure Canadian technology malfunctioning again. Don’t worry. We’ll be as technologically advanced and developed as Michigan soon!
@Elliot Williams – Sarcastic tone duly noted. :-) However, you do know humans can’t hear 60 nor 50 Hz? You are hearing a harmonic tone. There’s all kind of solutions for 50/60 Hz filtering. However, has any thought of using a mathematical sieve to extract “seemingly” random numbers? Here is some preliminary background:
So lets just say you generate an unusually large database of this, not 2.7 trillion, but large enough.
Next, you code a “sieve” to parse out a window of a few of these “seemingly random” numbers with a mid$ command that can return lets say 100+ characters to be used as your public key simple transposition seed. You can randomly move the window around via the text position start element to keep it O.T.P.(-ish). They would be all 2-digit numbers to correspond to the ASCII table chr$ numbers.. The plain text alphabet and numbers, etc. are transposed against it. Of course that’s the simplistic way of doing it. There are much more devious ways to make it even more complex.
These Pi number samplings have no mathematics relationship and you can’t text-find reoccurring patterns like with the letter E and such. However, it can be defeated though with state-of-the-art supercomputers, but not all that easily if the script-kiddy is not aware that’s what you are using in your public key. Your accomplice does not need sophisticated equipment or tradecraft to decipher the encrypted message. Any OTS computer should suffice. He just needs the private key from the sender. I think POTUS Jefferson would love this quasi-steganographic idea.
https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcQS_B4EDhHx7TUkwiDLVL8FhxEI7eZ4kYyvaMz43Vw2S1xKUbo9
One of the hackaday prize entries provides an implementation of this – http://hackaday.com/2015/06/29/true-random-number-generator-for-a-true-hacker/
Same author
https://hackaday.io/project/5588-hardware-password-manager
Haha, I didn’t even notice. I did wonder however why the writing style was similar.
Good stuff :)
Timer jitter can also be used, and it can provide random numbers at any time, not just at startup. Here’s a good starting point for Arduino, Teensy and Raspberry PI platforms:
https://sites.google.com/site/astudyofentropy/home
two ten meg resistors in series between supply and ground. Cmos input opamp with unity gain attached to the resistor divider where the two resistors connect. Output to A/D channel. Use the least significant bits from 16 reads.
Should be darned random..
Replace one resistor with zener diode. Set opamp for a lot of amplification and AC bypass input. Much noise will appear, but will require some postprocessing to make it uncorrelated and thus truly random.
maybe another aproach is to make white noise and conect do A/D chanel
Isn’t this kind of method highly susceptible to external manipulation? (Like an RF field or something).
Would be hard to do this in a predictable way.
not sure what is about RNGs that make them so interesting to research, human condition perhaps?
Big companies audit their stockrooms with random numbers. A truly RNG would not turn up the same stock number (unless it was truly by randomness). A Psuedo RNG will, on occasion, keep hitting the same parts bin, and not the one next to it. If the randomly selected parts bins concur with what the database shows, one can be confident the other bins are similar. High value items, such as the bin that holds cut diamonds, are checked on a routine basis, such as hourly. B^)
You can have a poor TRNG and you can have an excellent PRNG.
And how about using quantum noise of any P-N junction? One can combine this with RF white noise by making a crystal radio with germanium diode connected to an amplifier and then to ADC input. One ciuld use a reverse-biased PIN diode with sample of radioactive isotope.
My concern is with the power up ram states of each bit being correlated across start up events. Say slightly different threshold voltage on the individual fet transistors would pre dispose some to power up in one or the other state.
To me this reads as a typical ” I built my own encryption system and even I can’t break it so it must be secure”.
If you put a low entropy source through a couple of improvement steps, you can quickly reach the 7.9999 bits/byte level. For crypto applications, the bad guys will actually TRY to defeat your scheme.
Example: suppose we have a true RNG that provides us with 8 bits of entropy. F(0) = RANDOM(8bits). Next we run it through a good PRNG: F(t+1) = AES (F(t), “mysecretkey”) .
If you analyse the results with measures like bits/byte, you’ll see that the resulting sequence is very good random sequence. But there are only 256 seeds. So derive a key from this “random” sequence and your adversary will know you have only 256 possible keys.
> While it might not be good enough for crypto applications, it still
> generates high enough entropy for amusement games, simulations,
> art gadgets, etc.
Well, if you’re going for non-crypto-randomness, just grabbing a few ADC conversions, microsecond resolution timing events and adding those as entropy to a reasonable (crypto?) PRNG will give you way better-than-required random numbers for an “amusement game, simulator, or art gadget”.
It looks to me there are a bit more than 256 seeds here.
I would be inclined to use something like a variable-length markov chain to see how predictable those ‘good’ random-looking bytes really are.
The diehard and ENT suites perform far more sophisticated randomness tests.
Certainly, but he ran the diehard suite on the output of a PRNG seeded by his random generator. Assuming the PRNG is good, the diehard test will pass, regardless of seed quality. Running diehard on the seed generator would be difficult as it needs a very large amount of bits to work. It would take extremely long to collect this entropy.
No, tests were performed on TRNG output. For the first test (two 8-bit PIC MCUs), the first PIC switched the other one off-on for 625,000 times, which took 50 hours, and the raw output data was tested.
has anyone thought to use the static on a webcam image or even that of an optical mouse?
yeah thats a common one, theres a famous one that used a webcam pointed at a lava lamp
.
https://www.google.com/patents/US5732138
Look up SGI LavaRAND. They built a system using several genuine LavaLamp Lites and a webcam, which they de-focused a bit and fiddled with the color saturation.
The idea was to use chaotic natural motion, viewed through a very noisy camera, to produce truly random data. I participated in an IRC chat (in the #userfriendly channel on undernet) with one of the SGI people who built the system. This was late 20th century, circa 1998~1999. No idea if anyone would still have a log.
The SGI person did mention that after proving the concept they built another one for a “major financial institution” and to satisfy government regulations they had to write maintenance and servicing instructions (including exact procedures for changing the light bulbs) to ISO standard. Despite the proven security of the system, the client insisted on having the CD-ROM drive containing the disc with the encrypted data enclosed in a microwave oven, triggered by the alarm system on the door to the room. Break into the room instead of using the (I assume random of the day or other time period) security code and *zzzzap* goes the data you’re attempting to steal.
Nevermind that to be able to decrypt the data a thief would not only have to carry off the entire system, he’d also have to *precisely duplicate* everything within the field of view of the webcam. The positions and angles of the camera and the lamps, the mounting fixtures for the lamps (they had to be secure so they couldn’t tip over), the walls of the room, *everything* the camera could see would have to be duplicated. SGI explained the microwave wasn’t needed but the “major financial institution” insisted. (A setup like this would have been the perfect thing for an episode of “Chuck”, but it would be unhackable even with The Intersect.)
Of course the camera could have simply been pointed at a busy street outside the building and picked up data every bit as truly chaotic, but that wouldn’t have involved LavaLamp Lites. :)
SGI maintained their own LavaRAND system for a while, with a website where anyone could download chunks of random data, and they had a “magrathea” page that used it to generate random (but not seamless) images that could be used for “planets” in 3D rendering. (Just turn the seam to the back, nobody will notice.)
There was also a LavaRND, based on but not connected with LavaRAND – but both are long gone.
I remember writing a BASIC program decades ago on my Timex-Sinclair 1000.
It would grab a “random” number (from its RNG) print a square on the TV screen, and repeat.
(I wondered how long it would take to completely fill up the screen- it didn’t)
I did notice patterns develop on the screen the few times I ran it.
Then I wrote a reverse function of the program, select a random number and erase the square from that location on the screen. It never did fully clear the screen. I don’t recall if I noticed a pattern in the erasure.
I did the same on a Sinclair Spectrum, plot a dot at a random X and Y. After playing outside for a few hours the screen was full of diagonal patterns of repeating dots. As you mention, if it was random it would have filled the screen, it didn’t, just started over with the pattern. I should have set it to XOR each point, was easy to do (OVER 1). Maybe I’ll do it on an emulator at 100x speed.
The equation for the PRNG itself was published in the machine’s manual. Something to do with 75, I remember. As most PRNGs do, it fed each result back into the seed. You could use the RANDOMIZE function to initialise the RNG to a value, or with no value it used the number of 50Hz interrupts counted since switch-on.
Well, no, a truly random would not fill the screen, well maybe in a thousand years…
That was my error in logic…
No but it should fill most of it, not just the 40-50% I observed. I suppose the screen coverage% by time would end up like a bell curve, as more pixels ended up covering existing ones, the very last ones taking forever to get done.
Then again there were plenty of good games for it. But if you’re thinking of doing strong encryption on a Sinclair Spectrum, DON’T use the built-in random function.
It’s actually an instance of the “coupon collector’s problem”. For a 320×240 screen, then, the expected number of iterations would be 76800/76799 + 76800/76798 + … + 76800/1 ~= 908,251.
wonder what effect decapping the ram chip would have.
Or having an uncapped RAM chip on the board just for this purpose? It wouldn’t need to be the same calibre (size, speed, etc. such as a chip that is EOL)
Now this is great HaD content. :)
Great article!
Regarding TR seed generation following a soft reset:
“Luckily, it is very unlikely that the contents of RAM will ever be exactly the same, as there is always some “housekeeping” part of RAM (or at least MCU registers) which will be affected by program flow.”
Speaking generally (not PIC-specific), be careful reading memory-mapped MCU/peripheral registers to generate a seed. Reading some registers may destroy register contents, alter flags, etc. Duh, right? Perfectly obvious when dealing with these registers specifically. Yet it’s the kind of thing that might just slip your mind when deciding on a *memory range* to scan, and decide “more is better, so let’s just read every accessible address!”
Wow. As always, a great article by Voja. Keep em’ comin!
how about feeding a white noise signal into a microcontroller and have it sample the random voltages and convert it into a string of numbers.
“[…] microcontrollers do have a source of true randomness inside them. While it might not be good enough for crypto applications […]”
Make up your mind :)
Good enough for a game or random network address, not good enough for high security. Mind made up.
This is a really good post, very interesting topic. I think I’ve seen this mentioned somewhere before, after I did some research into why a global variable was a different value every power up! Good to see an in-depth and proper hackaday type post instead of the endless and dull posts about 3D printing and Arduinos.
@Voja Antonic – Very interesting approach. It will take me awhile to fully understand it though.
@ET AL – One approach is to still use pseudo-random numbers, but make them incredibly hard to reverse engineer even with a supercomputer (though not impossible). One approach would to mathematically use a “modified sieve of Eratosthenes”. That way no external hardware would be needed, just software. It’s all generated internally in the computer using simple math. However, to do this efficiently you would need a system that could handle incredibly large numbers and do it quickly. I’ve only done it on a DEC VAX using FORTRAN. Anything less than that would take figuratively forever to generate a pseudo-random number matrix of a good size and in a timely fashion.
Why a “modified” sieve of Eratosthenes? Well a basic sieve of Eratosthenes is a simple, ancient algorithm for finding all prime numbers up to any given limit. In my case you would conversely look for NON-prime numbers up to a limit. In other words, you would start with an incredibly large non-prime number (the very last digit is divisible by more than 1 or itself should prevent it from being a prime number) and use the sieve to test it with a standard divisor (of your choosing) to output non-primes. A prime is only divisible by itself and 1 (that particular quotient would be rejected in the sieve script). The output matrix would be several sets of numbers that are non-primes and are divisible by many other numbers.
The larger numbers may have way too many digits for you to use for whatever application you need it for, so you could also test for quantity of digits (i.e. length) and aim for smaller sets. However, you could just concatenate the results to form a truly difficult to reverse engineer set of numbers that *looks* truly random (but is actually not), This modified sieve could take DAYS or WEEKS to generate using a convention computer system. However, I did it on a DEC VAX and it took literally seconds. I think a Beagle Bone might qualify but not sure. Also FORTRAN can deal with incredibly large numbers. But there may be other modern compilers or interpreters that can too.
The neat thing about the output numbers is that they could also be used for a text encryption algorithm**. The public-key would be the encrypted text being sent but the private-key would be a dual number – the large starting number and the smaller standard non-prime divisor number you chose. Both private-keys would need to be transmitted to the recipient in 2 separate communication channels to avoid outsiders decrypting the public-key using simple math.
—————————————————
**Ideally the encryption algorithm would just convert the unencrypted alphanumerics to 2-digit ASCII numbers, concatenate it to a large real numeric string. Then add a single non-prime suffix digit to prevent prime number sieve error. Now this number is treated as your *starting large number* to sieve.The resulting quotient matrix (only one of them is used) could be selected to send as a public-key (what the world sees). The divisor that was used in the sieve is your private-key. You could test for the smallest length of digits as a text compression method too. A more complex sieve would also run different smallest divisors coupled with a smallest quotient to compress long messages into to smaller ones. You decrypt by reversing the process and multiplying the public-key by the private-key, then transposing the 2-digit fragments from ASCII back to clear text. This method *seems* unbreakable (and is for a human using a calculator or paper), but not for a supercomputer working days and days on it (there is no detectable recycle-rate typical with standard pseudo-random numbers and no alphanumeric character repetition like the letter ‘E’ for example). Of course HUMINT (human intelligence) could defeat it by just getting the private-key from the sender some how.
—————————————————
I hope I explained this simply enough. I may not have used standard math jargon and rote-learners tend be be confused by autodidact polymath people talking outside the box.
SOTB
Please don’t try and invent your own cryptosystems unless you’re a cryptographer.
There already exist cryptographically secure pseudorandom number generators. They’re less byzantine and more secure than your proposed solution, and don’t require huge computing resources. A really trivial example is to iterate a secure hash function such as SHA1.
However, sometimes you really do need actual random data – if only to seed your CSPRNG. It doesn’t matter how good your PRNG is; if all instances start with the same seed, they’ll all produce the same results.
“Any one who considers arithmetical methods of producing random digits is, of course, in a state of sin” – John von Neumann
@arachnidster – That’s why I said I was a “autodidact polymath” as a caveat of sorts.
I agree my method is “byzantine” or even a bit older than that. However, standard “secure pseudorandom number generators” I’ve been told have a serious flaw. I think it is called a detectable 28-day recycle rate or something. That simply means that a supercomputer can detect the PRNG is recycling numbers in the SAME pattern some 28 or so days into it. Maybe I don’t have that right but I think that is the gist of it.
Of course I would never disagree with John von Neumann, however, I’ve seen arithmetic random number generators based on a clock timer and a math algorithm that makes it APPEAR to the uninitiated that the numbers are truly random when they are apparently not. I’ve seen a programmer use a MS EXCEL macro to do this to generate a “rolling number” password system. The remote party would have the same EXCEL macro running on his/her system, have a PC/MAC clock based on a time standard like ‘time.nist.gov’, and the rolling password would be large, in synch, and apparently based on a random number system as the password is never the same twice, not even in 28 days.
I guess the idea is to ‘fool’ the outsider human into thinking it is truly random, and only a supercomputer can tell the difference. I think truly randomness was designed in the SIGSALY machine as they used recordings of arc light electrical noise. But you’d have to have an exact replica recording on the recipient side for it to work. That’s why I prefer pseudo-random numbers that don’t recycle after a number of weeks.
SOTB
Calling yourself an “autodidact polymath” is basically shorthand for “I think I’m very smart, but I don’t want to take the effort to communicate clearly with others, so I will make it your responsibility to try and interpret what I’m saying”. It’s not helpful.
There is no such thing as a “28 day recycle rate” in any commonly used CSPRNG I’m aware of. Why would it even be tied to calendar days in the first place?
Cryptography is a well established field with both a lot of research and a solid foundation. If you want to criticise and improve upon it, that would be very welcome – but please take the time to understand it first, rather than proposing your own system from scratch and declaring it superior based on no real evidence.
@arachnidster – I wouldn’t disagree with you on the “autodidact polymath” thing. However, I am no Leonardo da Vinci. I’m more of a Christopher Michael Langan. I like to be helpful however I’m afraid my seemingly non sequitur style of communicating is confusing to some. That’s were the “autodidact” part fits I guess (i.e. means self taught not necessarily smart). I don’t like ‘tooting own horn’ to the benighted so I verbally (or textually) obfuscate just a bit to avoid that. I’m sure you get it…
The 28-day recycle mentioned was from a RSA Labs engineer (Bedford, Massachusetts), . He was not talking being tied to calendar days. He was just referring to how pseudo random number generators tend to inherently start all over again in the same pattern within about a month or so in a predictable way. You can find this in rolling password systems.
I wasn’t criticizing today’s cryptology systems. I know many of them are pretty darned strong. My approach was an old endeavor back in the good old days when American NSA was allegedly suppressing prime number math in American school system to prevent budding ‘hackers’ I guess. Hell, we Americans (aka Yanks) didn’t even know of the NSA’s existence hence the nick name NO SUCH AGENCY until US Sen. Frank Church pointed it out to US. My approach is in no way SUPERIOR (or proposed as such) to any system today. It was just an old idea I was kicking around about 3 decades ago. I just thought it was intriguing. I was researching Pierre de Fermat at the time and I was dabbling in all forms of math at the time too – being an autodidact. RSA even had a 1991 initiated RSA Factoring Challenge which ended in 2007. I guess in an autodidact way I was paralleling that (somewhat) without knowing it.
If I’m not mistaken (and I probably am), banking systems use a cryptology-based numbering system close to my approach. I think the “powers that be” obfuscate the mathematics of it all to thwart laymen and would-be computer criminals from figuring it out and using it in a nefarious way. But of course my autodidact-style prevents me from being “accurate” or at least stick to the “party-line”.
I think Alan Turing was so cool!
No, banking systems use cryptographically secure PRNGs just like all other secure cryptosystems. I’m still somewhat baffled by your “28 day” assertion – why would you even relate it to a time period at all? I might call my PRNG once a day or a thousand times a second; one is going to exhaust it sooner than the other.
All PRNGs have finite repeat intervals because they have finite state. It’s trivial to design one with an arbitrarily large interval, though, simply by having a lot of state: the Mersenne Twister, a common non-cryptographic PRNG, has a cycle time of 2^19937 − 1, meaning no plausible process will ever cause it to repeat.
@arachnidster – I was debating with myself on whether to use the word cryptographic versus cryptologic. I guess you solved that for me. More self-taught dilemmas? (LOL)
The 28-day (+ or -) recycle was an approximation by my RSA contact. I think he was referring to a rolling password (RP) system running non-stop 24 x 7. Of course RP systems use PRNG. He wasn’t saying it was a design-feature. It was just an intrinsic mathematical probability after about a month of continuous generation of multi-millions of numbers.
This was over a few decades ago so the technology of the time was probably 64-bit I think (or even less). So maybe I’m still working on legacy memory of yesteryear. I haven’t spoken to this fellow since then. I’m sure things have probably progressed on a level of magnitude since then.
I guess when you’re self-taught a lot of things get left out in your education as it is not formal as going to university and getting the “party-line” version.
BTW truly random numbers can not be used for live communications encryption as they can not be reproduced by the recipient UNLESS they have a EXACT replica of the random numbers or its audio image in a recording (See: American SIGSALY machine during WW2). However pseudo-random numbers can be reproduced live by the recipient via prearrangement but not easily by an outsider (See: German ENIGMA machine also WW2 vintage).
POTUS Thomas Jefferson invented a really amazing encryption machine in 18th century using a quasi-pseudo-random arrangement which utilized the ancient encryption art of Steganography. (See: Jefferson Wheel Cypher). It helped us beat the Brits here in USA and abroad. :P
A common use of secure random numbers is to generate a public/private key pair, which can then be used in communications.
@Artenz – I agree, but TRUE random numbers or PSEUDO random numbers? As I said TRUE random numbers need to have a set of at least 2 images (i.e. audio etc.) for sender and receiver to use to communicate. However PSEUDO random numbers can be reproduced on the fly by prearranged methods and no 2nd image is needed. However, standard pseudo-random arrangements tend to recycle patterns after a time making them flawed in the face of supercomputer number crunchers today. So any system that would remove that flaw would be impressive.
OFF TOPIC: I think the only unbreakable system is still OTP systems. There is a OTP from WW1 that was delivered by carrier pigeon but recently found it’s body in a chimney. It’s OTP message strapped to it’s leg is still unbroken today. The Voynich manuscript doesn’t count as a unbreakable code as the NSA claimed recently. It was just misunderstood who the author really was. No code at all actually..
There are cryptographically secure pseudo random numbers. As long as you have a true random seed, they can generate a virtually unlimited stream of random numbers. Even with just 64 bits of state, you can generate a million random numbers per second, and still not repeat until the sun blows up. And it’s very easy to use a few thousand bits of state.
@Artenz – OK I get what you’re saying. However, the salient point remains the same: if you introduce “true random seed” (TRNG seed) to a pseudo random number generator (PRNG) aren’t you defeating the purpose of a PRNG? I mean ideally you don’t want to replicate the American SIGSALY machine which had 2 exact recordings of true random noise which was synchronized to the US NAVAL CLOCK. The recipient must have an exact image of sorts to decipher the spoken encrypted message. Otherwise the message remains unintelligible gibberish. With PRNG there is a way of reproducing the decipher “key” on the fly by the recipient because he is given the private key secretly by the sender. Or the outsider could reproduce it through supercomputer number crunching and predictable repetitions in the cipher text. The word PSEUDO means false or mock. I can’t see how a TRNG would be helpful unless you were using the dual-image TRNG method of SIGSALY. Google: SIGSALY for more information.
I’m not sure if my RSA contact was talking about 64-bit or 128-bit when he mentioned about PRNG repeating there PRN pattern after about a month of running non-stop. He gave me 2 RSA key fobs to play with. The rolling password numbers stopped after about 2-years or so. Don’t know why. Planned obsolescence? I mean RSA is an American corporation. That’s just how we Yanks roll I guess. :-)
Not to take away anything you did in this article, but Microchip already has a true random number generator in some of their parts …like what’s on the PIC24FJ128GA202.
http://www.microchip.com/pagehandler/en-us/technology/embeddedsecurity/technology/hardwarecryptoengine.html
Thanks Girmann, it’s something I didn’t know about. I downloaded the 24FJ128GA204 family manual, but at a quick look I didn’t find about how do they generate TRNG. Either they didn’t publish it or I have to dig deeper.
i see thermal noise http://ww1.microchip.com/downloads/en/DeviceDoc/60001246A.pdf
I’ve found it, and I like it, as it also uses multiple ring oscillators (probably two-oscillator system modulated by thermal noise, or something like VIA V3 with four oscillators).
I’m sure, I missed it, but isn’t this approach fundamentally flawed? RAM content is not truly random after power-up, but depends to some degree on the content it held before the power-loss. The degree depending on time of power-loss and temperature, I believe. Goes by the handle ‘cold boot hacking’.
Yes, the article mentions similar disadvantages when the power is only dropped for a short moment. But this can be fixed by storing the random number state in the RAM as well, so that the hash covers both ‘random’ RAM, as well as the previous data. Given enough bits and a good hash, this should be good enough.
Whether it’s good enough for crypto depends on what you’re trying to protect.
In a simple implementations, the analog to digital converter is sufficient:
http://mikrokontrolery.blogspot.com/2011/03/epp-generator-losowy-program.html
http://mikrokontrolery.blogspot.com/2011/04/generator-liczb-losowych.html
Couldn’t you just hook up a light sensor, temperature sensor, etc and take the last few decimal places of the reading for a random number? You could have multiple and combine the numbers to create larger random numbers. For instance, you have a temperature sensor that reads 72.5946023544 F. This number is always varying, because the temperature in the room isn’t constant. You take the last 4 decimal places, 3544, and there’s your random number. I realize you couldn’t read a temperature sensor to that many decimals, but its just an example. It is never going to create a predictable pattern because its based on something unpredictable.
The point is how to generate the random numbers with no external hardware (even no port pin usage), using MCU internal resources only. Of course you can hook up any kind of sensor and use ADC output, but it’s too straightforward to deserve hacker’s (-a-day:) attention.
Hear hear Voja! For sure the designer could implement many of the suggestions here, WITH EXTRA HARDWARE, even if that is only a couple of resistors, a zener, or whatever. This solution you’ve suggested generates a sufficiently random number (importantly on powerup, and without user interaction) with ABSOLUTELY NO OVERHEAD except some code. No extra pins. No hoping your timers are not going to lock together (like 556’s used to). No temp sensor or A/D converter? No problem!
It might be an old solution, but you’ve done it justice. It is *exactly* what I’m looking for for my *very* heavily constrained project that needs a random number on power-up.
Well done Voja!
for a truely generated number would it not be achieveable from subtracting or multipling or even both the current live time and date at any gived period no time of day is exactly the same when the date is also intrduced. at this time of post 01:20 on the 12/07/2015 the math we use to generate a truely random number devide the time by the date =9.94034550155877e-6
Why all that fuss with RAM ? Couldn’t some simple external source of noise be used ( noisy diode etc) and A/D sampled, for example ?
Instead of fiddling with RAM, could a Brownian Motion producer (say a nice hot cup of tea) be more suitable for a project that I’m working on. I call it the “Infinite Improbability Drive”.
+42
Some 40 years ago, in Hobby Electronics magazine, there was this schematics of a “digital white noise generator”, consisting of simple cmos ic’s, XOR gates and a shift register as I recall, plus a clock. It was in effect a pseudo-random bitstream generator. After breadboarding it and listening to the white noise, I started playing with the gates ins and outs, and I even managed to listen to some pseudo-random music 😄