In the wee hours of the late 17th century, Isaac Newton could be found locked up in his laboratory prodding the secrets of nature. Giant plumes of green smoke poured from cauldrons of all shapes and sizes, while others hissed and spat new and mysterious chemical concoctions, like miniature volcanoes erupting with knowledge from the unknown. Under the eerie glow of twinkling candle light, Newton would go on to write over a million words on the subject of alchemy. He had to do so in secret because the practice was frowned upon at that time. In fact, it is now known that alchemy was the ‘science’ in which he was chiefly interested in. His fascination with turning lead into gold via the elusive philosopher’s stone is now evident. He had even turned down a professorship at Cambridge and instead opted for England’s Director of Mint, where he oversaw his nation’s gold repository.
Not much was known about the fundamental structure of matter in Newton’s time. The first version of the periodic table would not come along for more than a hundred and forty years after his death. With the modern atomic structure not surfacing for another 30 years after that. Today, we know that we can’t turn lead into gold without setting the world on fire. Alchemy is recognized as a pseudoscience, and we opt for modern chemistry to describe the interactions between the elements. Everyone walking out of high school knows what atoms and the periodic table are. They know what the sub-atomic particles and their associated electric charges are. In this article, we’re going to push beyond the basics. We’re going to look at atomic structure from a quantum mechanical view, which will give you a new understanding of why the periodic table looks the way it does. In fact, you can construct the entire periodic table using nothing but the quantum numbers.
The Quantum Numbers
We are all used to seeing various drawings and diagrams of atoms with the nucleus surrounded by electrons whose orbits take the shape of concentric circles. While this description is useful in some situations, it is not an accurate description of an atom. The most significant problem with this model is the visualization of the electron in a concrete location. In quantum mechanics, the location of the electron orbiting an atom is described by its wave function, which gives only a probability of where you might find it. This concept is called electron density. The square of the wave function reveals the distribution of electron density in a three dimensional space around the nucleus, and is called an orbital. This distribution can be calculated via the [Schrodinger] equation, whose results form what is known as the quantum numbers.
There are three different quantum numbers:
- Principal (n) – The size of the orbital.
- Angular Momentum (l) – The shape of the orbital.
- Magnetic (m) – The orientation of orbital in space and the number of orbitals.
The values of the three quantum numbers are given in integers. The principal quantum number (n) determines the size of the orbital and its values can range from 1, 2, 3 and so forth. The angular momentum (l) and magnetic (m) numbers are dependent on the principal number. For l, the value is a range from 0 to (n – 1). These values are denoted as letters s, p, d, and f. The m value range can be found with the equation (2l + 1), and the values will follow ( –l…0…+l ) . Once you do the math, you can construct a chart that is much easier to understand:
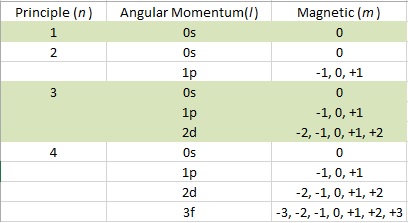
There is a 4th quantum number that is unrelated to the above three called electron spin. It’s written as +1/2 and -1/2. All electrons have spin and they can be only one of these two values. This spin will play a key role a bit later. For now, we need to understand a little more about how the orbitals exist in space.
Orbital Shapes
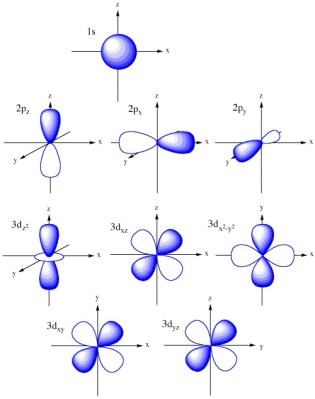
According to our chart, there are four different values of l, or four different orbital shapes. The simplest is s, and is spherical in shape. In the n = 2 shell, the p orbital is available and looks something like a peanut. For this orbital, it can have three different values of m. Remember, the m number tells us the orientation in space. But more importantly, it tells us the number of orbitals that are available. In the case of p, the m value is -1, 0 and 1. So we can have up to 3 orbitals on the xyz axes of a Cartesian system. Moving on up to n = 3 puts us at the d sub-shell and gives us up to 5 orbitals. With n = 4, the f sub-shell can hold up to 7 orbitals. Take a look at the image to the left to get a visual idea of what these orbitals look like in space. Note the f orbital is not imaged as it is difficult to visualize.
Once you understand how the quantum numbers give rise to the orbitals, we can move on to see what happens when we fill them up with electrons.
Electron Configuration
We now have enough knowledge to begin solving the periodic puzzle. But first, we must pay a visit to the lab of Mr. Wolfgang Pauli and acquire a key piece of (often overlooked) information. His Pauli Exclusion Principle tells us that no two electrons can have the same quantum number. What does the even mean?
Well, let’s take a look at the simplest atom – hydrogen. It has one proton and one electron. In its lowest energy, or ground state, the electron will exist in the smallest orbital s in the n = 1 shell. The next element in line is Helium with two electrons. Mr. Pauli says no two electrons can share the same quantum numbers. Now let us remember the 4th somewhat obscure quantum number of spin. This allows the two helium electrons to share the same s orbital in the n = 1 shell so long as their spins are opposing. When two electrons share the same orbital (with opposite spin), they are said to be paired. On an unrelated note – this pairing gives the electrons a very interesting and somewhat mysterious property that would spark a paradox that came close to bringing all of quantum physics to a halt. I go into detail about it here if you need a little more light reading.
We now have enough knowledge to build the periodic table from scratch. The electron configuration for hydrogen can be written as 1s1, where:
- 1 = The principal quantum number (n) or shell.
- s = The angular momentum number (l) or sub-shell.
- 1 = The number of electrons in the sub-shell.
Helium would be 1s2. This will fill our n = 1 shell, and now we must move on to the n = 2 shell. Lithium and Beryllium would be 1s22s1 and 1s22s2 respectively. Now the s sub-shell in the n = 2 shell is full. The next available orbital is the p sub-shell. So Boron would be 1s22s22p1. We can carry on filling the orbitals as such:
- C = 1s22s22p2
- N = 1s22s22p3
- O = 1s22s22p4
- F = 1s22s22p5
- Ne = 1s22s22p6
Now we’ve reached our first Noble Gas, Neon. Notice the entire p sub-shell is full. Why is it full? Because the p sub-shell has three m values. Each of these is an orbital, and two electrons can fit in each orbital. A full p sub-shell means two things. 1) Neon should be very stable and 2) we must move to the n = 3 shell. You should now be able to figure out the electron configuration for Sodium – 1s22s22p63s1. You should also notice that we’re repeating a lot of information. It is customary to use the last Noble Gas to abbreviate the core electrons. In the case of sodium, we would write Na = {Ne}3s1.
If you keep on going, you can build the entire periodic table. Consider the image below.

Here we have the periodic table showing only the valence, or outer electrons in each element. It is these outermost electrons that determine an element’s reactivity. Some patterns should stand out. Take a look at the Noble Gases in the right magenta column. All (excluding He) have a completely full p sub-shell. This explains why they won’t react with anything. The elements in the column to the left of it in light green are known as the halogens. Halogen means ‘salt producing’ and, because they only need a single electron to fill their p sub-shell, are highly reactive. Where can they get that single electron? How about an element with only one valence electron, such as the ones in the yellow left most column. Does NaCl ring a bell?
As you see, one can take the entirety of the Periodic Table of the Elements and begin to understand how elements relate to and react with each other via the configuration of the valence electrons. While many of the relations have been known for hundreds of years, it wasn’t until the development of quantum mechanics that we understood precisely how the electrons were configured within each element. It is amazing to think how this level of understanding of what nature is made of can be traced back to a very simple question with a profound answer – “Is it a particle or wave?”
Sources
Chemistry: Atoms First, by Burdge Julia. Chapters 3 & 4, ISBN-9781259208416

















Plumes, not “plums”.
Smoke plums everyday
What’s a vowel between friends? Haha, fixed.
However n should be the “principal” quantum number, not “principle”.
Got it, thanks!
You made my week
Although Newton never publicly converted lead into gold, many natural philosophers copied his recipe of converting lead into a fruity plum smoke. It was very popular at social events of the day. If it was correctly timed with a rapid drop of temperature and pressurr, the smoke would condense into a plum rain. Giant punchbowls still exist as artifacts of this phenomenon. Plums, not “plumes”.
This is where J.J. Thomson came up with the plum pudding model for the atom!
Purple rain, purple rain!
It always comes back to Prince.
Shout out to http://nuclides.org/
Ok, yes, “Not a hack”…but hell, its nice to wake up to a fundamentals reminiscence in a readable review. Thanks, Will. It’s greatly appreciated.
One question that has always left me confounded is, knowing the properties of the elements, how can you predict the properties of combinations of the elements?
From a simplistic view, electronegativity can be used to predict bond types, and therefore strength. Once you get beyond simple diatomic molecules complexity increases. In some respects it also decreases. Once you know C6H6 forms a benzene ring you can predict how it will interact with other molecules based on the electron affinity of a given molecule.
But in truth, you need a lot more information than just a detailed periodic table. You need bond energies, quantum mechanics, statistics, and 200 years of experimental data.
“Once you know C6H6 forms a benzene ring you can predict how it will interact with other molecules based on the electron affinity of a given molecule.”
It’s also the shape that helps you figure things out as well: you can guess that atoms forming a ball or ring can hold other atoms inside – hence the behavior of stuff like buckyballs, but also molecules like chlorophyll, which has a ‘trap’ containing a magnesium ion. But you can imagine it’s pretty easy to ‘pop out’ that magnesium ion with free charges in a solution, or acids. And it is.
A lot of biology/medicine is just geometry as well – you get a molecule of the right size to fit right inside something else.
Yes, getting the right molecule to fold or unfold a protein is the key to preventing many diseases.
Not only that, but getting the right sequence of the protein. You can think of genetic diseases as bugs in your computer coding, except that biology allows for some bugs to get through so evolution works. Unfortunatly, some of the bugs tend to screw things up. Sickle Cell Anemia arises from a single mutation that flips a hydrophobic amino acid (usually sticks into the protein) to a hydrophilic amino acid (likes water, sticks out of the protein) Normally, this might be a minor issue, especially for such a large protein complex as hemoglobin (something like 540 amino acids) However, this particular mutation can allow the mutated amino acids to stick to one another when your blood oxygen level is low, and you get this growing chain of hemoglobin filaments that stretch the blood cell into the sickle shape. Interestingly enough, it has been shown that sickle cell anemia might be an evolutionary defense mechanism against Malaria, since the malaria parasite incubates inside of red blood cells and causes cells to sickle spontaneously if you have half of the mutation, signaling to your liver to destroy the cells. So, if you have half of your genetic code “messed up” to code for sickle cells, you can live a fairly normal life and have a defense against malaria. However, if you have both sets of code set for sickle cell, you develop full sickle cell anemia.
Evolution: Natures way of going “Eh, I’ll just force compile and hope for the best.”
Some wit observed “Hydrogen is a colorless, odorless gas that, given long enough, begins to think about itself.” As others have commented, knowing the size and bond-forming properties of atoms lets you make some predictions about the type of simple compounds it will form, but the eventual complexity of those substances as a physical system is far too complex to predict.
Well, there are mathematical methods used in theoretical/quantum chemistry, that allow you to calculate such properties even for large molecules. Most popular are pure ab initio methods like Hartree-Fock, perturbational methods like Moller-Plesset, partially experimental like Density Functional Theory and so on. It’s quite complicated, large molecules require powerful computers and quite a time to compute, subtle effects require theory modifications.
It can be used for example to design and verify new drugs, calculate thermodynamical properties of non-standard compounds.
If you’re interested there are quite a few opensource solvers, that you can run on your pc, like PSI4 and try it yourself.
Loved the article, once I got past the non-sequitur of the first part concerning Newton and Alchemy, but any writing on the subject that doesn’t at least mention Mendeleev is missing the heart of the subject. Mendeleev created the concept of the periodic table looking at chemical properties. That we continue to find uses for this masterwork speaks to its genius.
The periodic table is my favorite graph!
Yeah, that was a hack … extracting patterns from apparent chaos and trying to make some sense from that patterns.
I agree, Mendeleev predicting even the undiscovered elements was quite a feat. They may have been trying to reduce article length.
A curious article on a rare subject for HaD, thanks. But I have to voice my discontent too. [Mendeleev] figured it out and he deserves a mention.
valence not valance
There was one rogue in there, huh? Fixed.
correction: Newton the late 16th century guy is in reality a 17th century guy,
-> born on 25.12.1642 and died in † 20.3.1726 it makes him a late 17th and early 18th century scientist.
Because actually the year 1642 lies within the 17th century, as we started with the 0th century during the year 0..100
Actually .. we started with the 1st (first) century during the years 0…100 – you meant the right thing and then Freud turned you down :-D
Actually the whole thing started in 525AD. Pope Dionysius Exiguus did a bit of highly reliable Christian maths, and decided that, from history as they knew it, Jesus was born exactly 525 years ago, so this must be the year 525. He was doing it to make figuring out when the hell Easter was more simple. Round about the year 800AD Dionysius’s system took off, and people forgot about whatever system they were previously using (based around root vegetables probably) and stuck to the lovely new AD system.
Obviously since Jesus didn’t do many miracles when he was born (just a few), nobody thought about completely restarting the calendar around him.
Good catch. Thanks!
principle -> principal
“Notice the entire p sub-shell is full. Why is it full? Because the p sub-shell has three m values.” Nobody really knows the “why” of any of this. You might consider something along the lines of “Our formula says it is full because it has three m values”.
And as long as we are all copy editors, “alchemy was the ‘science’ in which he was chiefly interested in” :-)
You could dig up all the formula that predicted the shapes of the quantum orbits; and compare that to the images of electron orbits from new microscopy techniques. I’d say the theory of how and why is defined in the numbers, and proven in observation.
People have seen electron orbits with microscopes!? I admit this is a bit past where my knowledge runs out, but I thought electrons only had orbits in theory, in “reality” they’re in a superposition, a cloud of potential existence.
The terminology “orbitals” confuses people. Orbitals are wavefunctions and as such are purely just mathematical functions with no physical realization. They aren’t measurable.
Just the probability density.
The fact we used to think of atoms as little solar systems doesn’t help the confusion. And they’re still drawn that way in textbooks.
A preposition is a very bad word to end a sentence with!
“According to our chart, there are four different values of l, or four different orbital shapes. The simplest is s, and is spherical in shape.”
This is true, but drawing it as a sphere is misleading. It’s definitely spherically symmetric. It only matters *how far* you are from the nucleus. But where’s the *peak* of the probability density – at what position do you find the electron most often? At the center! That’s why I say it’s misleading: it’s not a uniform ball, but it’s always drawn that way. That ‘radius’ is just a characteristic radius of how fast the probability falls away.
And the ‘l’ quantum numbers mean the *angular momentum* of the electron: and for ‘s’, that number is *zero*. It doesn’t have *any* angular momentum. So how do you end up with something going around and around without any angular momentum?
Answer? It’s not going around at all. It’s going in a straight line, back and forth, right through the nucleus. Just like someone on a swing, a pendulum, or an oscillating spring. The wavefunction is a sphere because the orientation of that straight line is random – whenever you interact with it, it’s going to end up in a new orientation. So when you image the thing, it’s going to look like a ball. But on its own, you *should not* think of the electron flying around the nucleus in a circle. It’s not. It’s zipping in a straight line, back and forth.
It’s a similar thing for ‘p’ shells too: the electron isn’t whizzing around that ‘dumbbell’ uniformly. It’s just like someone swinging back and forth on a swing, and you push them to the left or right when they’re away from the center. (I don’t have any intuition for higher shells, though – the swing analogy breaks down then, I think).
I find that for many purposes, it’s best to dispense with the idea of thinking of an electron as a discrete particle (Heisenberg making an appearance here). Instead imagine it as a “cloud of negative charge”, denser in some parts than in others — the orbital pictures describe the shape of that cloud by choosing an arbitrary density cut-off (e.g., “90% of the electron density lies within this shape”) rather than an all-or-nothing boundary.
This becomes particularly important when you start dealing with the orbitals of poly-atomic molecules, which have a much more complicated shape and much less obvious symmetry.
The problem with that is that it still gives the wrong impression of the ‘s’ state, which has its *highest* probability at r=0. It’s really not a 3D shape at all, which of course makes sense since it has no angular momentum to *give* it a shape.
It’s really just a problem with the ‘s’ state, though, as that’s the only one that has that problem, because it’s best visualized as a 2D rather than 3D object. Visualizing the others as distributed clouds is a great way to do it, and it helps with the completely non-intuitive stuff like the p orbitals never being in the nucleus.
I should also point out that it’s a bit misleading even for me to say “you find the electron most often at the center” – because in a 3D sense, the actual volume at the exact center is 0. And if you convolve the falling probability with the volume of the area enclosed, obviously there is a “shell” that the electron is found in more often than not – e.g. here:
http://hyperphysics.phy-astr.gsu.edu/hbase/hydwf.html
But that gets back to the point, actually: when you see that you tend to think that the electron is never in the nucleus – the nucleus is at r=0, after all. So if you think of the electron like a cloud of negative charge, you immediately think “oh, there’s no part of it in the nucleus.” And then you wonder why the hell something like pionium or muonium just dies immediately. Pionic hydrogen (a pi- meson bound with a proton) especially.
But again, it’s just like a kid on a swing. The kid passes through the ‘center’ all the time – but the kid also spends less time there because he/she’s moving so fast at that point. So the chance of ‘finding’ the electron near the nucleus is super-small – *but that doesn’t mean it isn’t passing through there*. Pionic hydrogen dies immediately because the pion just whacks a proton.
That’s why I said just looking at the ‘cloud’ as the interpretation isn’t always the best way. It tells you where the electron’s charge will get distributed, but the electron can interact with things even though it has no chance of being there.
I don’t understand or remember the f block placement nor why the s block fills before the d and p blocks but why the d block fills before p. It seems to me that either the f block should totally precede the d block and so that two rows that include f-block elements should be *f1-*f14 /then/ *d1-*d10, not *d1, *f1-*f14, *d2-*d10.
Anyone want to fill me in on this?
This piece made a number of simplifying assumptions / omissions, and one of these relates to your question.
The order in which the blocks “fill” depends on energy… electrons fill the orbitals in order of increasing energy, so as to obtain the lowest overall energy level. On the surface one would expect that this means first filling the 1s orbital, then the 2s orbital, then the three 2p orbitals, then 3s, etc., and this is indeed what happens for the first row or two of the periodic table.
Farther along, though, a few other principles start to rear their heads: one is the idea that half-filled and completely filled orbitals have particular stability, and the other is that the strict ordering of energy levels by n and l breaks down at higher atomic numbers.
This is why you see unusual configurations for the lanthanides and actinides. Across the row of lanthanides you generally have a half-filled 6s orbital and are steadily adding electrons to the 4f orbital (adding electrons to 4f is energetically more favourable than adding to the next available d and s spots). It also explains why Cu and Zn have d10 s1 and d10 s2 configurations.
There’s more to be written on this topic but that’s probably enough for now.
The blocks aren’t filling in order at all. The atoms are filling electrons to lowest energy. Blindly you might think that means filling all orbitals (s, p, d, f) before going to a higher energy level. And that works for hydrogen all the way up to argon: 1s through 3p.
But past that, it actually takes more energy to add an electron with so much angular momentum to be in the ‘d’ shell that it’s lower energy to fill the 4s shell first. And *then* the 3d shell fills, and then the 4p shell fills.
It’s actually trickier than *that*, though, because *the author is missing a quantum number* – the spin quantum number (s). That’s what allows 2 electrons to be in the same shell. And sometimes it’s slightly lower energy to have just 1 electron in an orbital than both of them – obviously they repel each other, and if the orbitals have them forced close together often, that’ll be higher energy.
So, for instance, chromium’s configuration isn’t just “1 more electron in the 3d shell.” Its lowest energy configuration has an unfilled 4s orbital (even though vanadium, before it, has a full one), and 2 more electrons in the 3d shell, because it’s lower energy to have 2 unfilled orbitals (the 4s and a 3d) than have them all full.
Thanks guys, that’s precisely what I needed to hear!
The words you want to look up are the “Aufbau principle”
1s
2s 2p
3s 3p 3d
4s 4p 4d 4f
5s 5p 5d 5f …
Now, in terms of energy, start drawing diagonals down from the top right. Energy levels fill in the order 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, and so on. So, an atom with 5 shells will fill the 5s shell before the higher energy state that is the 4d shell. But, an atom with only 4 shells will fill 4s, then 4p, then 4d.
APPLIED QUANTUM LAB HOLIDIUM
Orbitals can also be understood as the various resonance states of a 3 dimensional drumhead.
Oh good! That makes it so simple!
I don’t know enough about the topic to recognize it would pass peer review or not. Let’s say it passes peer review, are the there going to be follow up articles illustrating how a builder-hacker- maker can incorporate this knowledge as they go about designing their projects? Then again I’d have to guess if one’s project doesn’t make use of complex chemical reactions this article is a general knowledge article, hopefully helping us understand why things are done the way they are done. I wouldn’t read too much into Newton opting for becoming director of the mint over thee professorship, no doubt many brilliant minds choose the financial sector of the education sector today with income being a part of the decision.
It does help to mention that Lithium and Beryllium have a 2p0 shell, which is why they bond. Otherwise, Beryllium with a full 2s shell looks like it should be a nobel element having it’s upper most shell filled.
Ahh, the joys of having a Chem 101/102 professor who loved the quantum model. This brings back so many memories.
Great post !
Yes we stand on the shoulder’s of giants!
‘Principal’ ≠ ‘Principle’.
In my research work I discovered a direct connection between JJ Thomson’s plum pudding model and the entire periodic table. Look for “correspondences between the classical electrostatics Thomson problem and atomic electronic structure” on arxiv and a poster of electron energies of mine the curator of “the internet database of periodic tables” for a very useful poster and summary of how this work may have an impact on many things.
We can get the entire periodic table with just one “shell” of electrons.
Quantum numbers aren’t exactly the bookkeeping system of atoms….we know of she’ll filling Ruke violations.
Not is Pauli’s exclusion principle generally true across the periodic table. Even quantum mechanically we know these things. My work demonstrates that the exclusion principle can be obtained by classical means.
This is a good article.
Has anything ever been proven without observation?
observation itself changes any subject.
Science is an unobtainable thought, yes thought of a mad person.
It can be explained but never proven only changed by the observer.
Prove that wrong.