You would think that there’s nothing to know about RGB LEDs: just buy a (strip of) WS2812s with integrated 24-bit RGB drivers and start shuffling in your data. If you just want to make some shinies, and you don’t care about any sort of accurate color reproduction or consistent brightness, you’re all set.
But if you want to display video, encode data in colors, or just make some pretty art, you might want to think a little bit harder about those RGB values that you’re pushing down the wires. Any LED responds (almost) linearly to pulse-width modulation (PWM), putting out twice as much light when it’s on for twice as long, but the human eye is dramatically nonlinear. You might already know this from the one-LED case, but are you doing it right when you combine red, green, and blue?
It turns out that even getting a color-fade “right” is very tricky. Surprisingly, there’s been new science done on color perception in the last twenty years, even though both eyes and colors have been around approximately forever. In this shorty, I’ll work through just enough to get things 95% right: making yellows, magentas, and cyans about as bright as reds, greens, and blues. In the end, I’ll provide pointers to getting the last 5% right if you really want to geek out. If you’re ready to take your RGB blinkies to the next level, read on!
Gamma
If you’ve ever dimmed a single LED using pulse-width modulation (PWM) before, you have certainly noticed that the response is non-linear. If you ramp up the duty cycle from 0% to 100%, it looks like the LED gets brighter very quickly in the beginning and then somewhere around the 50% mark stops getting brighter at all. On a WS2812, with its eight-bit-per-color resolution, stepping from a red value of 5 to a red value of 10 more than doubles the apparent brightness, while stepping from 250 to 255 can barely be noticed at all.
It’s not the LED or the PWM controlling it that’s to blame, however. It’s your eyes.. We perceive brightness using some kind of power law: if B is perceived brightness and L is the luminance — the amount of physical light that’s getting through your irises — the relationship looks roughly something like this:
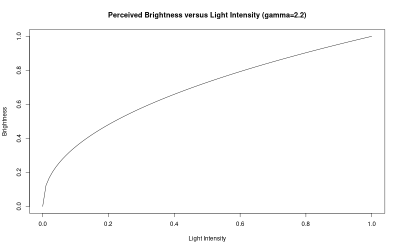 That exponential relationship, requiring more and more additional light to create a perceptible difference in brightness, is characterized by that Greek exponent: gamma. For your intuition, gamma values from just around 1.5 to around 3 are probably reasonable to consider. Arbitrarily picking gamma to be 2 makes that fractional gamma exponent into a more comfortable square root and usually isn’t too far wrong. 2.2 is a standard value for CRT monitors in the PC world, and 1.8 used to be the standard for Macs.
That exponential relationship, requiring more and more additional light to create a perceptible difference in brightness, is characterized by that Greek exponent: gamma. For your intuition, gamma values from just around 1.5 to around 3 are probably reasonable to consider. Arbitrarily picking gamma to be 2 makes that fractional gamma exponent into a more comfortable square root and usually isn’t too far wrong. 2.2 is a standard value for CRT monitors in the PC world, and 1.8 used to be the standard for Macs.
But if you really care about the way your LEDs look, you’ll want to tweak the gamma to your particular conditions. I like to think of choosing a gamma in terms of black-and-white photography. If we gamma-correct with a value that’s bigger than your eye’s natural gamma an image will look too contrasty — there will be jumps in the brightness where you’d want it to be smooth. If the gamma is set lower than your eye’s gamma, differences will be muted, and it will look muddy. Get it just right, and you get a smooth transition from dark to light across the full range.
Taking the 2.314’th root of a given number is a tall task to ask of a microcontroller, though, and it’s probably overkill. In the end, I usually implement the gamma correction as a lookup table that turns the desired brightness directly into whatever numbers the chip’s PWM routine wants, so there’s no math left to do at all at runtime. Here’s a quick and dirty Python script that will generate the lookup table for you.
Now in Color
 Gamma correction can make your single-color LED effects look a lot better. But what happens when you step up from monochrome to RGB color? Imagine that you’ve gone through the whole gamma experiment above with just the red channel of a WS2812 LED. Now you add the green and blue LEDs to the mix. How much brighter does it seem? If you weren’t paying attention above (yawn, math!) you’d say three times brighter. The right answer is the gamma’th root of three.
Gamma correction can make your single-color LED effects look a lot better. But what happens when you step up from monochrome to RGB color? Imagine that you’ve gone through the whole gamma experiment above with just the red channel of a WS2812 LED. Now you add the green and blue LEDs to the mix. How much brighter does it seem? If you weren’t paying attention above (yawn, math!) you’d say three times brighter. The right answer is the gamma’th root of three.
Strictly speaking, computing brightness depends on the mix of light coming out of all three LEDs. The good news is that you can also figure out the brightness of any arbitrary color combination with gammas. Here’s the formula:
Given any ratio of red to green to blue, you can use this formula to work out the PWM values for each LED that you need to brighten or dim the overall color in equally-sized steps.
Cross-Fading
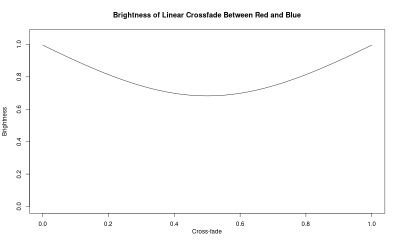 The other use of the brightness formula above is in fading from one color to another, keeping the perceived brightness constant. For instance, to fade from red to blue naïvely, you might start at (255,0,0) and head over toward (0,0,255) by subtracting some red and adding the same amount of blue. Plugging those values into the brightness formula, the result appears significantly dimmer in the middle: down to about 70% of the brightness of the pure colors. Unfortunately, this is the way that nearly everyone online tells you to do it. That doesn’t make it right. (Or maybe they just don’t care about brightness?)
The other use of the brightness formula above is in fading from one color to another, keeping the perceived brightness constant. For instance, to fade from red to blue naïvely, you might start at (255,0,0) and head over toward (0,0,255) by subtracting some red and adding the same amount of blue. Plugging those values into the brightness formula, the result appears significantly dimmer in the middle: down to about 70% of the brightness of the pure colors. Unfortunately, this is the way that nearly everyone online tells you to do it. That doesn’t make it right. (Or maybe they just don’t care about brightness?)
A great way to figure out the gamma that you’d like for RGB LEDs is to set up a color fade and adjust the gamma until there is apparently uniform brightness across the strip. In fact, you can do this with just three LEDs. To make the effect most dramatic, it helps to start with medium brightness on either end of the fade: I’ll use (70,0,0) and (0,70,0) for instance. The middle LED should be some kind of yellow with equal parts of red and green. Tweak the amounts of these values until you think that all three LEDs are about the same brightness, and you can solve for your personal gamma.
Color Palettes and Lookup Tables
 On a slow microcontroller, or on one that should be doing more important things with its CPU time than computing colors, constantly adjusting color values for brightness is a no-go. In the single-LED case, a lookup table worked well. But in RGB space, a three-dimensional array is needed. For a small number of colors, this can still be workable: five levels of red, blue, and green produces a palette with only 125 (53) entries. If you’ve got flash memory to spare, you can extend this as far as you’d like.
On a slow microcontroller, or on one that should be doing more important things with its CPU time than computing colors, constantly adjusting color values for brightness is a no-go. In the single-LED case, a lookup table worked well. But in RGB space, a three-dimensional array is needed. For a small number of colors, this can still be workable: five levels of red, blue, and green produces a palette with only 125 (53) entries. If you’ve got flash memory to spare, you can extend this as far as you’d like.
An alternative workaround is to gamma-adjust the individual channels first. This gets the brightness right, but it also affects the rate at which the hue changes across the cross-fade. You might like this effect or you might not — the best is to experiment. It’s certainly simple.
Color Sensitivity and Other Details
For me, getting control of the brightness of a color LED is about 95% of the battle. The remaining 5% is in getting precise control of the hue. That said, there are two quirks of the human visual system that matter for the hues.
The situation with the cross-fade of colors is actually more complicated than I’ve made them out to be; the eye isn’t uniformly sensitive to each wavelength of light. If you mixed together 10 lumens of red, 10 lumens of green, and 10 lumens of blue, the result would look overwhelmingly blue. The good news is that this effect is so strong that monitor and RGB LED manufacturers pre-weight the amount of light coming out of each LED for you.
So when you assign a value of (10%, 10%, 10%) to an RGB LED, each of the red, green, and blue LEDs are on for 10% of the time, but the green LED is about three times brighter than the red, and ten times brighter than the blue. The LEDs used take care of the (rough) color-balancing for you, so at least that’s one thing that you don’t have to worry about.
Perceptual Uniformity of Hue
 If you’re trying to encode numerical values in colors, however, there’s one last quirk of the human perceptual system that you might want to be aware of. We are more sensitive to differences in some colors than in others. In particular, hues around the yellow and cyan regions are really easy for us to distinguish, while different shades of reds and blues are much more difficult. Getting this right is non-trivial, not least because our perception of one color depends on the colors that it’s surrounded by. (Remember the “white and gold” dress?)
If you’re trying to encode numerical values in colors, however, there’s one last quirk of the human perceptual system that you might want to be aware of. We are more sensitive to differences in some colors than in others. In particular, hues around the yellow and cyan regions are really easy for us to distinguish, while different shades of reds and blues are much more difficult. Getting this right is non-trivial, not least because our perception of one color depends on the colors that it’s surrounded by. (Remember the “white and gold” dress?)
Anyway, here’s a library that does pretty darn well at addressing the perceptual uniformity of hues issue, given they’re constrained to using piecewise linear functions. They sacrifice some degree of uniform brightness to get there, though.
If you just need a few colors along a perceptually uniform color gradient, Color Brewer has your back. Python’s matplotlib is going to change its default color scale to one with significantly increased perceptual uniformity and constant brightness, and this video explaining why and how has a great overview of the subject. It’s not simple, but at least they’re getting it right.
Finally, if you’d really like to dive into color theory, this series has much more detail than you’re ever likely to need to know.
Conclusion
You can get lost in colors fairly easily, and it’s fun and rewarding to geek out a bit. On the other hand, you can make your LED blinky toys look a lot better just by getting the brightness right, and you do that by figuring out the appropriate gamma for your situation and applying a little math. The “right” gamma is a matter of trial and error, but something around two should work OK for starters. Give it a shot and let me know what you think in the comments. Or better yet, use RGB-gamma-correction in your next project and show us all.
















What is that Eye-Sphere thing, and has it been covered by Hackaday before? If not.. where did it come from?
https://learn.adafruit.com/led-tricks-gamma-correction
Its a POV sphere that was featured years ago i believe
I tried looking for it, but io cant find it sorry. Pretty sure i remember seeing it before though…
http://cousins-sears.com/the-orb
https://www.ted.com/talks/nick_sears_demos_the_orb?language=en
Great article! Gamma is ignored far too often.
One of the problems with the LEDs with integrated drivers (WS2812 for example), is that you have to do gamma correction outside the chip – the 8-bit control value is used for linear PWM by the chip. This cuts down the number of perceivable levels you can get (as you mention, it’s compressed at the top of the range). A better LED chip would have gamma built-in, say using the sRGB gamma curves, so that you can still get 256 levels out, gamma corrected, and approximately perceptually uniform.
I’ve implemented LED drivers in PICs, for instance, with an integrated gamma correction, and fit a dynamic range of over 25,000:1 into an 8-bit brightness control. I’d really like to see the commercial driver chips do something like this; they only have a 255:1 dynamic range as it is.
Hi, are those PIC drivers open source?
Thanks for taking the dive into the widely complex world of color perception.
Good article. I had to do some work in this area back in the games industry developing a lighting model for low-end hand-held devices that didn’t cause all the artwork to look crap at low light levels. Problem was we didn’t have data sheets for the display devices in question, so gamma had to be determined experimentally. That was done by locking myself in a darkened room, drawing an alternating cross-hatch pattern on the left-hand side of the screen (i.e. half the pixels at 0 and the other half at 255) and then increasing the level of all the pixels on the right-hand-side of the screen until they visually matched in brightness; that gave the gamma mapping at the 50% mark. Repeat the process for 25% (i.e. 0 and 128 crosshatch) and 75% (128 and 255) and then just recurse until you have 9 readings for each RGB channel across the entire range (including 0% and 100%, which map directly). Map the resulting curves, apply an exponential curve-of-best fit and there’s your gamma value for the display.
Apparently, gamma was originally developed for non-linear output of CRT displays and only coincidentally happens to be close to what is needed to correct for human visual response. The appropriate transformation to apply for psychometric lightness is CIE 1931. https://en.wikipedia.org/wiki/CIE_1931_color_space
Not sure what came first, but gamma was an important part of photographic film studies. We conducted various measurements of different brands and types of film and paper, and plotted out the gamma curves for comparison.
Ah this brings back memories from almost 30 years ago when I had to devise a system to match Pantone swatch color codes (which were reflected light values) with the spectral output from photographically produced backlit displays. Oh boy was that fun, so many nonlinearities that in the end I wrote some code to produce tables of color patches on a 4K Matrix Instruments PCR Film Recorder then used a densitometer to find the section of a given table that contained a range that covered the target values, I’d then produce a new table to expand that range. Basically it was a divide and conquer approach.
Anyhooo back to now, given we have the convenience of digital cameras with raw output and well documented color profiles it should be possible to categorise the curves for any set of LEDs so that we know what output to expect for any given setting used for the circuit we are powering them from. This will give us a table that removes all of the characteristics of the LEDs over the illumination range used, we can then apply a second table to account for the response of the human eye. Separating the tables makes sense as the eye data does not change but the LED data may on another project.
Great article. I haven’t yet gotten around to building anything pretty with those controllable RGB LEDs, but I’m bookmarking this article for when I do.
I was happy to read that the LEDs internally correct for the eye’s different sensitivity to RGB (prior to reading that point, I was thinking that your equal-brightness colour fade was very wrong…).
But you have a mistake in here: “So when you assign a value of (10%, 10%, 10%) to an RGB LED, each of the red, green, and blue LEDs are on for 10% of the time, but the green LED is about three times brighter than the red, and ten times brighter than the blue.”
Should say that green is 1/3 as bright as red. The eye is most sensitive to green.
Y = 0.2126R + 0.7152G + 0.0722B
(from the linked colour FAQ)
His phrasing is correct: you have same PWM, therefore green appears 3 times brighter. It appears brighter due to sensitivity of the eye. It’s correct. it SHOULD BE 1/3 the PWM for same brightness.
Except “RGB LED manufacturers pre-weight the amount of light coming out of each LED for you.”
The Green LED is 1/3 the size of the red, to ensure that 100%, 100%, 100% PWM duty cycle gives white (instead of greenish yellow).
i wouldn’t trust that all rgb leds will have the same color ratios. I have seem some that tend to be very blue heavy.
Nice article but lots of small problems. E.g., the “lumens” to begin with is quite poorly dealt with; also the 2nd equation is not proper (B on both sides…).
Just a small math nitpicking: in the equation for brightness the letter B is used for both brightness and blue channel. Since not that many sy,bols are needed in the entire article, one could afford using some other notation for one of them.
Color Mixing and Matching. “RGB” LEDs packaged together will have much better color mixing (no rainbow effects) and come with matched RGB dies from the factory. Definitely not worth trying to go the discrete route if doing a RGB project.
Color-Fading is simply a visual effect. If making a monitor with RGBs, this effect can be ignored because you want to keep color accuracy. If the video signal says 50% red and 50% blue, your display should emit the gamma corrected 50/50. It should NOT increase red/blue values 43% to compensate for the 70% brightness issue. If it did, non-primary colors would appear too bright.
” It should NOT increase red/blue values 43% to compensate for the 70% brightness issue. If it did, non-primary colors would appear too bright.”
I’m confused about what that formula is for, then. Is (128, 128, 0) not any less bright than (255, 0, 0)?
For the gamma calculation I can recommend this simple script ;)
http://jared.geek.nz/2013/feb/linear-led-pwm
Why not importing math.h and use the logarithmus naturalis to do so?
Assuming r goes from 0 to 255:
convertedr = log(1+r)/5.545 *255
I went crazy getting the rgb values right on my project :
https://hackaday.io/project/6413-sliced-light-in-color
Now i see the reason why the inputed pwm values dont match the actual colors. Thanks for the post
I’ve read this article so many times recently. Really appreciate it. Question about gamma correcting individual channels though: You say it gets the brightness right but not the hue. Consider fading from red to green with yellow in the middle. Halfway, you will have something like (128, 128, 0). Gamma correct that down to something like (25, 25, 0), and you have a yellow which is much dimmer than (255, 0, 0) or (0, 255, 0). The yellow with the same brightness as the red and green would be more like (170, 170, 0).
It seems like the hue is right when you correct each channel individually but the overall brightness is off. Is that right?
This article and the comments are a goldmine, thanks all :-)
Some interesting invertigations into ws2812:
https://cpldcpu.com/2022/08/15/does-the-ws2812-have-integrated-gamma-correction/