For the last few months, I’ve been up to my neck in electronic conference badges. This year, I created the single most desirable badge at DEF CON. I also built a few Tindie badges, and right now I’m working on the logistics behind the Hackaday SuperConference badge. Sit tight on that last one — we’re doing something really, really special next month.
Most badge projects are one-off production runs. This is to be expected from a piece of hardware that’s only meant to be distributed at a single event. The Tindie badge is different. It’s now a thing, and we’re building multiple badges for all the cons and conferences Hackaday and Tindie are attending for the rest of the year. This means I have the opportunity to do hardware revisions on the Tindie badge. Right now I’ve built three versions of the Tindie and we’ve distributed about two thousand of these kits at DEF CON, Maker Faire New York, and the Open Hardware Summit.
After about two thousand units, I think we finally have this down. This is how I designed three versions of hardware in as many months and cut the BOM cost of each badge in half. This is bordering on a marginally impressive piece of engineering, and a great lesson on BOM cost optimization.
 The Tindie Badge, Mk. 1
The Tindie Badge, Mk. 1
 This is the first revision of the Tindie badge. I wrote about it on the Hackaday blog earlier, but the simple version is pretty much Jasmine saying, “Hey, we should build a Tindie badge for DEF CON”. It’s not like I didn’t have my hands full at the time, so I agreed to take on the project. We designed, ordered, received, kitted, and distributed three hundred Tindie badges in two weeks.
This is the first revision of the Tindie badge. I wrote about it on the Hackaday blog earlier, but the simple version is pretty much Jasmine saying, “Hey, we should build a Tindie badge for DEF CON”. It’s not like I didn’t have my hands full at the time, so I agreed to take on the project. We designed, ordered, received, kitted, and distributed three hundred Tindie badges in two weeks.
The Mk. 1 Tindie badge is just about as simple as it gets. There’s a battery holder, a battery, and two flashing RGB LEDs. Some BMP hacking in Eagle makes for a great PCB, and a ‘pin clasp’ soldered to the back of the PCB makes it a true wearable.
Kitting and distribution of this badge went great, and the BOM cost was reasonable: $1.83 per badge at quantity 300. Great for DEF CON, and a potential to be a *great* bit of swag. A lot easier to lug around than a bunch of t-shirts, in any event.
The Tindie Badge Mk. 2
 With the success of the Tindie DEF CON badge, we decided to make a few more up for our next event: World Maker Faire in NYC. Confident in our ability to put together badges quickly, our target quantity was 1,000. A thousand badges, and only a month and a half to get it together. Not a problem.
With the success of the Tindie DEF CON badge, we decided to make a few more up for our next event: World Maker Faire in NYC. Confident in our ability to put together badges quickly, our target quantity was 1,000. A thousand badges, and only a month and a half to get it together. Not a problem.
The changes from the Mk. 1 to Mk. 2 badge were purely cosmetic. While using layers of copper, silk, copper resist, and mask work well enough as an artistic board, I wasn’t quite happy with how the first version of the Tindie badge turned out. There wasn’t a whole lot of difference between the dark blue and light blue, the eyes could have used more definition, and Tindie’s rivets should look like actual rivets. This meant I needed to change some of the dark areas to tinned areas. Not a problem — it’s just playing around with Illustrator, BMPs, and Eagle.
The Mk. 2 badge for Maker Faire was a success, both as a bit of swag and from an engineering standpoint. Instead of the $1.83 the first version cost, the Mk. 2 version was only $1.23. We used the same suppliers for the parts, so really that’s just a quantity discount. This is still a significant cost reduction, and considering how many stickers we give away at events, this is a very attractive bit of swag.
Was I happy with it? No. The plan to put tinned copper everywhere didn’t pan out, and the original badge looked better. At the very least, the nose and ears should be dark blue. There’s only so much you can mock-up in Illustrator without having a finished board in your hands. Still, we made 1,000 for Maker Faire, and the cost per badge came way, way down.
The Tindie Badge Mk. 3
 Our next event after Maker Faire was the Open Hardware Summit in Denver. After that, it’s the Hackaday Supercon where we’re expected to make it rain robotic dog heads.
Our next event after Maker Faire was the Open Hardware Summit in Denver. After that, it’s the Hackaday Supercon where we’re expected to make it rain robotic dog heads.
The most important issue to fix was, of course, the art. The basic idea behind the art was to refine the design, make the nose and ‘inside’ ear dark blue, keep the rivets silver, and use the white silk a bit more. I wrote another Hackaday post on how to do this art in Eagle, and that went together pretty easily. We’re all happy with the results.
The Mk. 3 Tindie Badge is a major revision. We’re doing actual, real, hardware changes. What’s the biggest change? A switch. I’ve tested the Tindie badge, and a fresh battery will blink the eyes for days, but some people like to take the battery out for some reason. Whatever, we need a switch.

The requirements for this switch meant it had to be an SMD (so the front art wouldn’t be messed up) SPST switch. Smaller was better, and as with all the components, we’re looking for the cheapest option. We landed on an Alps switch from Mouser, available for $0.14 in quantity 1000. That’s cheap enough.
With board art we’re happy with and the BOM pretty much sorted, let’s do a cost breakdown for 1000 Mk. 3 badges:
| Part | Unit cost | Total Cost | Source |
| Bags | $0.03 | 44.96 | AliExpress |
| Tacks | $0.11 | 114.11 | AliExpress |
| Battery holder | $0.36 | 357.26 | Digikey BK-916-CT-ND |
| Battery | $0.17 | 170.35 | Amazon |
| 5mm LED | $0.02 | 49.80 | Amazon |
| Boards | $0.54 | 321.77 | Seeed |
| Switch | $0.14 | 144.00 | Mouser 688-SSSS810701 |
The total cost per badge, in quantity 1000, is $1.37, basically the same as the Mk. 2 badge, but adding a switch. Acceptable, but I’m still not happy with how much we’re paying for battery holders and switches. We’re going to roll with the Mk. 3 badge for Open Hardware Summit and Supercon, but I’m going to make a few changes to the BOM going forward.
Real engineering and BOM cost optimization
We’re not going to cut the BOM cost on the bags, tacks, or the LEDs. Those are already as cheap as they’re going to be. Likewise, the price of the PCB isn’t going to come down much unless we order more in obscene quantities. I shopped around for batteries before building the first one, and trust me, Amazon has really, really cheap CR1220 cells.
This basically leaves the switch and battery holder as the places where we’re going to cut costs.
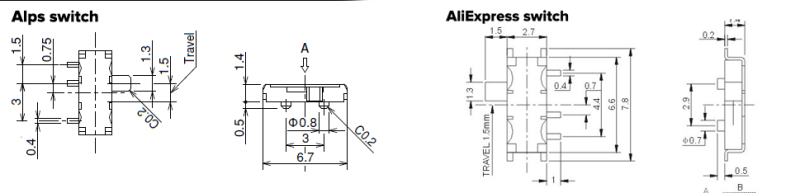
The first switch I found that fit the bill was from Alps, but quite a lot of electromechanical parts have a Chinese equivalent that’s more or less the same. After a bit of searching, I found this guy on AliExpress. Take a look at the drawings of both: No, they’re not identical. The ‘studs’ on the bottom of the switch are different; the AliExpress switch has 0.7 mm diameter studs, the Alps has 0.8 mm diameter studs. If you really study these drawings, they’re more or less the same. They’re effectively interchangeable, and if you make a part for one in Eagle, you have a part for both.
Here’s the kicker: I can get 1,000 Alps switches for $144. I could also get 1,000 of the AliExpress specials for $31.26. That’s $0.14 a badge for the Alps version, or $0.03 for the AliExpress version. I just saved eleven cents. For 1,000 boards, that’s a hundred and ten bucks. Awesome.
The biggest expense on the BOM is the board, and there’s little I can do to change that. The next biggest expense — by a large margin — is the battery holder. Not the battery, mind you: the battery holder. This is just a tiny piece of stamped metal, and it costs $0.36 in quantity 1,000. Unfortunately, AliExpress doesn’t help me here. The vast majority of CR1220 battery holders from the usual Chinese suppliers are plastic, through-hole components. I don’t want that; they’re bigger parts, they’ll ruin the art on the front, and they’re still pretty expensive at about $0.20 in quantity 1,000.
The battery holders for the Mk. 1, Mk. 2 and Mk. 3 badge were from Digikey. They work, they’re great, but you should always do a search on both Mouser and Digikey before designing something. (Or sign up for Findchips. That would have probably saved some money.) Here’s what I found on Mouser. It’s a different part from a different supplier, and it’s only for CR1216 and CR1225 batteries — not CR1220 batteries.
Those of you who know how the names of coin cells are derived are laughing right now, but here’s what’s going on. The first two numbers are the diameter. These batteries are 12 mm in diameter. The second two numbers are the thickness. A CR1216 battery is 12 mm in diameter and 1.6 mm thick. A CR1225 battery is 12 mm in diameter and 2.5 mm thick. Of course my CR1220 battery will work in a battery holder that accepts both 1216 and 1225 batteries. Why the Mouser part wasn’t labeled as being a CR1220 battery holder is beyond me.
The Mouser part is $0.19 in quantity 1,000, saving me $0.17 per board. That’s $170 in quantity 1,000. Let’s look at that BOM again, with the new parts:
| Part | Unit cost | Total Cost | Source |
| Bags | $0.03 | 44.96 | AliExpress |
| Tacks | $0.11 | 114.11 | AliExpress |
| Battery holder | $0.19 | 191 | Mouser 712-BAT-HLD-012-SMT |
| Battery | $0.17 | 83.35 | Amazon |
| 5mm LED | $0.02 | 49.8 | Amazon |
| Boards | $0.54 | 321.77 | Seeed |
| Switch | $0.03 | 31.26 | AliExpress |
| Total Cost: | $1.09 |
After three revisions, we’re happy with the art on our Tindie badge, and we brought the cost down and saved almost a dollar per badge. That’s really incredible, and a testament to how much you can save just by seeing what options you have available to you.
Don’t call them Diamond Dogs. That’s the wrong album.

What are the plans for the Tindie badge going forward? We’ve pretty much got the Supercon order lined up, and that’ll be the last con we’re going to this year. Next year, though, we’re distributing Tindie blinky badges far and wide.
The Tindie badges are some of the cheapest swag we have, and people love them. It’s a soldering kit, which fits in well with the whole, ‘make and sell hardware on Tindie’ thing we’re going for. These soldering kits are also much cheaper and much more easy to distribute than t-shirts. We’re aiming for several thousand by New Years, and we’re going to make it rain robotic dog heads.
This badge was an experiment. At the time I ordered 300 boards for the Mk. 1 Tindie badge, I had no idea how it would turn out. If we were doing these boards through OSHPark, it wouldn’t be a problem; [Andrew Sowa] already figured out how the purple PCB stackup looks when split into individual layers. Blue soldermask, though, is a bit trickier and demands experimentation. You can make reasonable guesses on how it will look in Photoshop, but it’s never quite right. I’m still not happy with the results, but some of my other pursuits are focusing on truly custom color PCBs and multicolor PCBs. Eventually, I’ll get something that looks fantastic.
Going forward, there are a few options for what we can do with the Tindie badge. I’m doing a few experiments with custom silk and solder mask, and I think this is the perfect platform to demonstrate a few new techniques. The top of the list for these experiments is an Aladdin Sane Tindie badge, a Kiss Army Tindie, and maybe one with the Mike Tyson face tattoo. Or Chakotay. I always get those mixed up. Look forward to multicolor Tindies sometime around March next year. That’s when the 2018 conference season starts up, and we’ll be distributing these things far and wide.

















Spoiler, they used cheaper parts.
See, this is what happens when Brian doesn’t write articles to inflame readers!
(crickets)
I’m sure somebody will find something to get angsty about.
Sorry Brian, but do we really need an article about your Tindie badge 2x a week?
;P
Great article. This is exactly the kind of stuff you have to sweat to get costs down. Next step: TaoBao! :)
“We’ll buy it from AliExpress” isn’t exactly rocket science, or “impressive engineering” for that matter.
No, but if you’ve never thought about how to go from 10 units to 1000 units, this article is very helpful. Logistics and part hunting aren’t often sexy. Little of what’s required to make a good product is just the engineering.
Brian writes an informative, non-inflammatory article about the process of refining versions of a project (that battery holder tip was great by the way) and people still complain. Yes it’s doesn’t cover bleeding edge hackery, but it’s well within the scope of the site. What is wrong with you all?
Agreed Conrad. I enjoyed the look into the process. If you don’t like every single article just move on to the next, this isn’t a site written just for you
MPD has a pretty large catalog:
http://www.batteryholders.com/search.php?cat=Coin+Cell+Holder
And some of their parts are cheaper than your original:
http://www.batteryholders.com/part.php?pn=BK-885&original=&override=
You should consider lead times for your purchases. They can point you to an entirely different direction.
https://www.digikey.com/product-detail/en/mpd-memory-protection-devices/BK-885/BK-885-ND/3829741
I did a badgelike project for a non-technical conference last year, to teach attendees to solder (and to get them to wear our logo framed by LEDs throughout the conference). The board was a small strip that was designed to sit at the top of the official conference badges. I did not want to pay for switches, so I designed it so that when attached, the lanyard clip would short two pads at the top, making the clip itself the switch. It worked well and the non-techies thought it was some kind of sorcery.
have not assembled mine yet from ohs. might need some hacky enhancements .. .
That reminds me, I need to solder mine up!
Can you make the safetypin thing into the switch?
Well I’ve seen two kinds of those, one where the pin is not very sprung and needs you to lock it with a rotating thing, and one where it’s well sprung to clip under, now if you soldered those down at two points on board and then cut between the points, you’d theoretically have a switch…
… but it would have either of the following faults when “off”… i) the pin would flop around and make contact randomly, or ii) the pin would be left sticking up all the time and you’d stab yourself on it.
Kids like this, is it possible to buy those badges somewhere?