What do you do, when you need a random number in your programming? The chances are that you reach for your environment’s function to do the job, usually something like rand() or similar. This returns the required number, and you go happily on your way.
number generator. [by KCAuXy4p CC0 1.0]
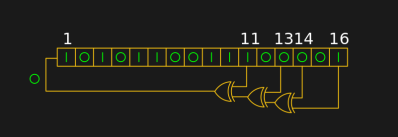
There is a handy way to deal with the PRNG predictability problem, and it lies in ensuring that its random number generation starts at a random point. Imagine the shift register in the previous paragraph being initialised with a random number rather than a string of zeros. This random point is referred to as the seed, and if a PRNG algorithm can be started with a seed derived from a truly unpredictable source, then its output becomes no longer predictable.
Selecting Unpredictable Seeds
Computer systems that use a PRNG will therefore often have some form of seed() function alongside their rand() function. Sometimes this will take a number as an argument allowing the user to provide their own random number, at other times they will take a random number from some source of their own. The Sinclair 8-bit home computers for example took their seed from a count of the number of TV frames since switch-on.

The Arduino Uno has a random() function that returns a random number from a PRNG, and as you might expect it also has a randomSeed() function to ensure that the PRNG is seeded with something that will underpin its randomness. All well and good, you might think, but sadly the Atmel processor on which it depends has no hardware entropy source from which to derive that seed. The user is left to search for a random number of their own, and sadly as we were alerted by a Twitter conversation between @scanlime and @cybergibbons, this is the point at which matters start to go awry. The documentation for randomSeed() suggests reading the random noise on an unused pin via analogRead(), and using that figure does not return anything like the required level of entropy. A very quick test using the Arduino Graph example yields a stream of readings from a pin, and aggregating several thousand of them into a spreadsheet shows an extremely narrow distribution. Clearly a better source is called for.
Noisy Hardware or a Jittery Clock
As a slightly old-school electronic engineer, my thoughts turn straight to a piece of hardware. Source a nice and noisy germanium diode, give it a couple of op-amps to amplify and filter the noise before feeding it to that Arduino pin. Maybe you were thinking about radioactive decay and Geiger counters at that point, or even bouncing balls. Unfortunately though, even if they scratch the urge to make an interesting piece of engineering, these pieces of hardware run the risk of becoming overcomplex and perhaps a bit messy.
The best of the suggestions in the Twitter thread brings us to the Arduino Entropy Library, which uses jitter in the microcontroller clock to generate truly random numbers that can be used as seeds. Lifting code from the library’s random number example gave us a continuous stream of numbers, and taking a thousand of them for the same spreadsheet treatment shows a much more even distribution. The library performs as it should, though it should be noted that it’s not a particularly fast way to generate a random number.
So should you ever need a truly random number in your Arduino sketch rather than one that appears random enough for some purposes, you now know that you can safely disregard the documentation for a random seed and use the entropy library instead. Of course this comes at the expense of adding an extra library to the overhead of your sketch, but if space is at a premium you still have the option of some form of hardware noise generator. Meanwhile perhaps it is time for the Arduino folks to re-appraise their documentation.
The subject of entropy and generating random numbers is one that has appeared on these pages many times. [Voja Antonic] made a in-depth study using uninitialized RAM as an entropy source for microcontrollers. If you have an insatiable appetite for understanding Linux entropy, we point you at [Elliot Williams]’ comprehensive examination of the subject.
[Arduino image: DustyDingo Public domain]
















“if a PRNG algorithm can be started with a seed derived from a truly unpredictable source, then its output becomes no longer predictable”
IIRC you only need to see N successive bits from an N-bit LFSR generator to deduce its state and perfectly predict the rest of the sequence. It doesn’t matter that you picked a truly random place to start.
But you also need to know both N and selected taps. One can customize his rand() function to increase the number of bits and select different taps for added unpredictability…
This is true, but the space is probably small enough to brute-force. Most people won’t use N above 32 or 64 so they can get away with using a single machine word for the shift register, so you have to try 64 different N’s. As for the taps, I don’t know how many maximal-length sequences there are, but most people will just pick them from a published table, since they don’t know how to find their own.
Actually, no, you don’t. You can use the Berlekamp-Massey algorithm from the output of any LFSR to find an equivalent one, assuming you have at least N samples, without knowing anything else about it. Not even the value of N.
It makes sense that something like that should be possible, but I had no idea it existed.
I wonder what would happen if you feed the first few bars of a MIDI file into it, let it produce an LFSR that generates those, then keep the LFSR running and listen to the output…
Also a PRNG and a LFSR are completely different. A software PRGN will repeat some numbers within it’s sample space.
A LFSR just re-organizes all of the numbers within a fixed sample space so the each one of them occurs exactly once in each loop of repetition.
In the example given, if you consider all of the bits to represent one 16 bit number for each permutation then the LFSR will yield all the numbers from 0 to 65536 exactly once before the sequence repeats.
To call a “LFSR” a RPNG you really need to have a register width many many times the required permutation space.
That’s not entirely correct, what you describe is a “maximum-length LFSR”. An LFSR doesn’t automatically have to go through *all* the numbers exactly once, but it will definitely at some point start over and enter a repeating sequence.
What is shown in the schematic is a what you describe as a maximum-length LFSR
That may be. But you said: “A LFSR just re-organizes all of the numbers within a fixed sample space so the each one of them occurs exactly once in each loop of repetition.” and my response was to that. What you described there is a maximum-length LFSR, and not just any kind of LFSR, and the one shown in the article just happens to be one of them.
Actually for a 16-bit maximal length LFSR you don’t get numbers 0 to 65536, it would be 65535. However, even that is wrong, since the values would be partitioned into two spaces, typically the degenerate case of “0” cycling back on itself, and the pseudo random sequence of the numbers in the range 1 thru 65535, repeating every 65535 counts.
Other maximal length taps chosen for the EXOR gates will sequence the numbers in a different order.
NON-maximal length taps will partition the space into two (or more) groups. A sequence in one group repeats without any values from the other, and vice-versa.
Don’t use an LFSR then. I wonder if Mersenne Twister or arc4random is usable on the Arduino (and if it would be faster to generate a number than to just wait for a new one from hardware!)
I don’t know about the latter, but Mersenne Twister is also predictable. Granted, you need around 600 outputs from RNG, but still, given enough time, this might become an issue. Cryptography is hard.
MT19937 is predictable because you can extract its internal state from observing a few hundred outputs. So it doesn’t matter how good the seed is.
If you want an unpredictable (cryptographically secure) sequence of digits, you must use a CSPRNG. MT is not a CSPRNG because its internal permutation function is reversible.
The short version is: if you want to build a CSPRNG, you need to have an irreversible function operating each step, which implies that you are destroying some state (and there are some other requirements). The usual approach is to use a cryptographic hash function, preferably keyed. HMAC-SHA* is currently considered to be an acceptable approach I believe. Yes, this is much more expensive than MT.
(PS sorry for flagging your comment)
Jenny,
A better test for AnalogRead() is to keep only the least significant bit and then check the distribution of zeroes and ones. If the 2 bins have equal count after 1000 or more bits it could be trusted.
Agreed. I once created a random number generator by taking the least significant bit of the system clock every time the connected Geiger-counter went off. Very simple, still very good.
ADC on an unconnected pin may show to a 50/60 Hz cycle, which can induce correlation/predictability in your random numbers. This may not matter. Depends on the application.
Timing of Geiger counts is very, very random if the clock you’re timing them with is very fast relative to the average count rate.
Very clever and straight-forward method.
Lovely.
My home-automation systems will totally have geiger counters in them :)
Dumb question – for hdw based rnd generators in general, not specific to the arduino issue described above: (Caveat: I program accounting apps, not cryptographic ones)
Why couldn’t the hdw rnd generator have one of the XORs be fed Least Significant Bit from the data bus and shift on every clock tick? Yeah you’d still be cycling through a finite loop of numbers, but given that it is constantly rolling along, within a few milliseconds of startup wouldn’t you be really hard pressed to guess the next number?
If you are going to use hardware, you can use forward-biased germanium or silicon transistor with floating base, a blocking capacitor and high-gain amplifier to get a quantum noise to be measured by ADC. Or reverse-biased PIN diode, high-gain amplifier and small source of radiation. First electronic random numbers generator used thyratrons in magnetic field to generate noise…
Zener diodes also have very high junction noise and are a lot easier to implement. Just use a narrow band analog read.
If you want true random then you can implement a Chua’s circuit –
https://en.wikipedia.org/wiki/Chua%27s_circuit
Chua is chaotic, but not random. It has attractors, which can give it undesirable statistical properties. On an X-Y scope, it’s awesome, though.
The traditional two-transistor white noise generator is really very good. I’ve built and tested four or five variations on this idea:
http://www.nutsvolts.com/magazine/article/bipolar_transistor_cookbook_part_5 (scroll to bottom)
This circuit doesn’t reject power-supply noise well, but runs “forever” on a 9V battery. The rest is signal conditioning, anti-tampering, and etc. But you can get 95% of a professional HWRNG with 20 cents worth of parts from your junk box.
A typical PN junction noise amplifier. I love that the chosen transistors are 2N3904’s. It shows that this is a very old reference. Of that era the equivalent none jedec transistor would have been a BC108.
How about forward biased (dimly lit) LED for a noise source?
Or even reverse biased as a light detector.
The problem with hardware based approaches like that (amplifying thermal noise)is patents. For a one-off you would be fine. For serious production, expect a call from lawyers.
Your idea of using the data bus sounds random, because who has a clue what’s on the data bus? Who keeps track of that?
But then if it’s protecting, say, the key behind some currency or information that might win a war, or whatever really really important thing, that’s not good enough. “I haven’t a clue what’ll come up” isn’t nearly good enough for unpredictable. You’re not a crypto expert (me neither) so of course you don’t know what will come up! But the enormous brains of crypto researchers are stuffed with all sorts of maths and tricks and discoveries. Crypto is used to secure very very important things, lots of money and brains have gone into inventing and then cracking it.
So any old random-sounding idea won’t do. You really need to get an expert to do it. There are people who decapsulate chips with nitric acid, fuzz inputs and power supplies, measure power consumption to the nano-amp. If your crypto solution is worth anything, it has to stand up to all of that. If it’s for something unimportant, then it doesn’t matter. But it’s fairly obvious that anything you or me could come up with, will have been done either better or easier by an expert.
That doesn’t mean “leave it to the experts” is true for everything in life. But crypto is incredibly specialised. For people who actually enjoy doing maths! Home-made crypto solutions are a non-starter.
My experience with Atmega analog inputs is that an open pin will convert to the same value as the previously sampled pin, probably because the sample/hold capacitor doesn’t get discharged through a high impedance input. So…YMMV on that. For most arduinoish projects that (I) make, I really just want to insure that each power cycle causes some different random-ness, so _any_ seed in a storm is fine. I usually use an analog input connected to an environmental sensor — light, temp, distance, etal — which will be somewhat different and usually a bit noisy as well. For some more entropy you can re-seed the generator periodically, or even pseudo-randomly.
Not good enough for cryptography, but certainly fine for government work…
The atMEGAs have in internal temperature sensor that is accessible. You can even access it from Auduino environment with some register writes.
What is clock jitter and how is it measures?
Clock jitter is generally regarded as any deviation from the expected clock behavior. In real life, it is a cycle-to-cycle variation. Suppose you have a 100 MHz clock, with a period of 10 ns. One period was might be 10.001 ns while the next would be 9.995 ns. Stuff like that. This is generally considered different from long-term changes in frequency, such as drift due to temperature, aging, voltage, etc.
I have once looked into a few different methods of random number generation. But generally, using a sensor to pickup noise from the environment is typically rather efficient. After all, to what I have read, PGP used user mouse movements as a source for randomness for its key generation.
A few other methods I wrote about sometime back over at: https://plus.google.com/u/0/105287714965102060733/posts/QQ5g9hdgtGy
Early PGP used to ask you to bash away at the keyboard for a while til it had collected enough randomness. It used precise timing of the period between keypresses, which is pretty random, but not a large source of random bits.
Many PCs have an option for spread spectrum on one or more of their clock speeds. Could that be tapped as a random noise source for generating random data?
Dither in these oscillators is not random. It’s cyclic, so no one frequency peks over others causing unwanted EMI…
A *suitable* PRNG would have a large seed value and a long repeat cycle – there’s quite a few … you should then seed this with multiple forms of entropy (reverse biased diode, blacked out CCD sensor, least significant bits of an interrupt counter) then “hash” them somehow. Then you reinitialise this often but on an irregular basis. voila … a nice set of random number numbers, :)
The Arduino Entropy Library on the AVR arduinos uses the watchdog timer in interrupt mode. This requires that the WDTON fuse not be set, and also prevents the WDT from being used for recovering from lockups as the library init puts the WDT into interrupt mode until the next reset.
I remember trying to use WDT randomness , but also needed the WDT, and I don’t think I was able to get it to work consistently. I then switched to uninitialized sram to generate the random seed .