Today is March 14th, or Pi Day because 3.14 is March 14th rendered in month.day date format. A very slightly better way to celebrate the ratio of a circle’s circumference to its diameter is July 22nd, or 22/7 written in day/month order, a fractional approximation of pi that’s been used for thousands of years and is a better fit than 3.14. Celebrating Pi Day on July 22nd also has the advantage of eschewing middle-endian date formatting.
But Pi Day is completely wrong. We should be celebrating Tau Day, to celebrate the ratio of the circumference to the radius instead of the diameter. That’s June 28th, or 6.283185…. Nonetheless, today is Pi Day and in the absence of something truly new and insightful — we’re still waiting for someone to implement a spigot algorithm in 6502 assembly, by the way — this is a fantastic opportunity to discuss something tangentially related to pi, the history of mathematics, and the idea that human knowledge builds upon itself in an immense genealogy stretching back to the beginning of history.
This is our Pi Day article, but instead of complaining about date formats, or Tau, we’re going to do something different. This is how you approximate pi with the Monte Carlo method, and how anyone who can count to a million can get a better approximation of one the fundamental constants of the Universe than Archimedes.
What Is Monte Carlo?
Before we dig into this, it’s important to describe what the Monte Carlo method of problem solving actually is. In short, it’s measuring or simulating some sort of system with the application of random numbers. Any sufficiently complete history of Monte Carlo method of problem solving begins with Buffon’s needle problem, but this example muddles the issue, and came about two hundred years before this sort of randomness was applied to statistical insight.
The true origin of Monte Carlo simulations came from the development of the hydrogen bomb in the late 1940s. Stanislaw Ulam is credited with discovering this technique when investigating exactly how much neutron shielding would be needed in a certain application. The problem couldn’t be solved, but there was a probability distribution for this system. The key factors of the design were known — how far a neutron would travel through a medium, and how much energy would be given off when colliding with the nucleus of an atom. The solution to this problem was to simply throw random numbers at the problem, letting the known probability distribution take care of the rest.
Working through an example of the Monte Carlo method is a much better way of understanding, so let’s do that. This is how you approximate a value for pi using hundreds of thousands of random numbers.
So How Do We Estimate Pi?
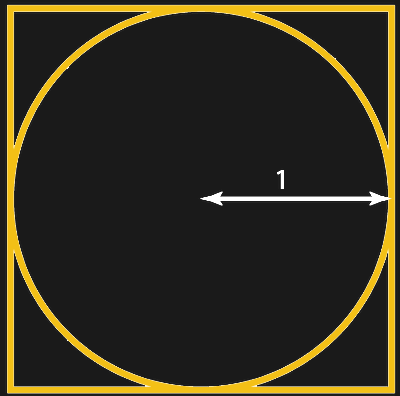
What we’re doing here is drawing a circle, with a diameter of two (a radius of one). This is commonly known as a unit circle. This circle is inscribed into a square with a side length of two. We place hundreds of thousands of random points inside the square, count the total number of points placed and comparing that with the total number of points inside the circle. Because we’ve chosen a radius of one, and the area inside the circle is , we can use
Total Points / Inside Points to give us an approximation of Pi.
If there’s one thing computers are good at, it’s counting. So with a little bit of Python, we can easily run our experiment:
import random as dot
import math as m
# Total number of random points.
total = 1000000
# Points contained in the circle.
inside = 0
#Main loop
for i in range(0, total):
# Place random dots in unit square
x2 = dot.random()**2
y2 = dot.random()**2
# Check if inside circle,
# increment counter if inside
if m.sqrt(x2 + y2) < 1.0:
inside += 1
# We're only doing positive x/y coords,
# so multiply by four.
pi = (float(inside) / total) * 4
# Print result
print(pi)
# Print difference
difference = m.fabs(pi - m.pi)
print(difference)
An explanation of what’s going on in this code should be in order. We set our total points at 1,000,000 and iterate through that range. Each iteration sets a random X and random Y coordinate and places the point on our plane. Determining the total number of points inside the circle is calculated with x² + y² < 1.0. If that equation is satisfied the “inside” points value is incremented.
That’s the jist of the above code, with one caveat; we don’t need to deal with negative x and y coordinates. We can simply ignore those, and multiply the ratio of the number of random points inside the circle over the total number of points by four.
After a few dozen runs of this small script, I rarely got a result that was off by more than 0.002. Most results ranged from 3.141 to 3.143. That may not sound impressive to anyone that can rattle off the first dozen or so digits of pi from memory, but consider the historical alternative. Archimedes’ best estimate for pi was 223 / 71 < π < 22 / 7, or two decimal places. Ptolemy calculated pi to three decimal places, and in the third century, Chinese mathematicians managed to figure out five decimal places. The Monte Carlo method, which is simply counting a dividing albeit on a scale no human should ever have to do, improves on any of these numbers. Do this, and you know pi to more places than Fibonacci.
A Truly Modern Technique
One thing that’s so easy to forget is that ancient people were just as smart as anyone walking down the street today. It’s not fair to discount ancient beliefs that whales are fish, that the Earth is flat, the value of mathematical constants, or even what our solar system looks like simply because someone lived a few thousand years before us. They simply didn’t know any better. Is it fair to criticize Archimedes for not calculating a better value of pi? No, and not just because it would involve counting to a million.
The Monte Carlo technique is an inherently modern technique. It involves randomness, and it’s not a mistake this technique was discovered when attempting to find a solution to a problem involving probability and quantum mechanics. The ancients simply didn’t have the tools to discover this technique.
It’s like the solution to Fermat’s last theorem, or a numeric solution for n > 2 in the equation an + bn = cn . A solution was finally found by [Andrew Wiles] in the 1990s, but it was completely unlike any sort of math Fermat would have known of, or anyone else on the planet for that matter. We don’t know if Fermat actually solved this problem, or what his proof would be, but it would have been so simple anyone could understand it instead of [Wiles]’s deep dive into obscure maths.
Could Archimedes have calculated Pi to a greater precision than anyone else by throwing marbles at a circle and square traced out in the sand? No. The knowledge we have today, and what children are taught in grade school, is built upon thousands of years of the brightest minds working on the hardest problems. Flashes of genius are so rare on a species-wide scale that scientific and mathematical advancement happens at a snail’s pace. We should hope that we’re not judged too unkindly a few thousand years down the line — we simply didn’t know any better.




















“and the area inside the circle is Formula does not parse ,”
But it does copy-paste, that’s interesting.
Fixed, thanks.
And coincidentally a very famous mathematician passed on this day.
Co-incidence?
B^)
… and that mathematician (or physicist) was coincidentally born exactly 300 years after Galileo’s passing…. Hmmmm…
There’s a complot theory to find in here…..
Which is on Einstein’s birth date too.
Now I wonder if they were all left-handed too.
Naturally, or out of necessity?
Since Einstein, we’ve known that there is basically no such thing as “flat” Euclidean space-time. If there’s mass or energy there, it’s warped. Since pi is only pi in flat space-time…while a useful concept – like Newton’s laws – it’s only an approximation, despite all kinds of elegant geometrical tie-ins (which all assume a zero mass-energy space).
Yeah, people don’t like to hear this kind of thing on what is otherwise a kinda fun, whimsical celebration, but it seems important to stay somewhat aware of our underlying reality.
I think I get your overall point (geometry is bigger than 2d planes?), but even without bringing Einstein, pi is an irrational number so it has *always* been only an approximation so I’m not sure why it changes things?
> pi is an irrational number so it has *always* been only an approximation
What you mean here is that approximations of pi have always been only approximations. Pi has a real value, and is not itself an approximation. If you write it as the symbol ‘π’, that’s not an approximation any more than ‘5’ or ‘x’ is an approximation.
No, he is saying that PI is COMPLETELY WRONG as the ratio between the circumference and diameter of a circle, because in a non-euclidean relativistic rotating reference frame the circumference of a circle increases relative to the radius as the angular speed increases. It is known as the “Ehrenfest paradox”.
First you may be write about the physics involved but the circle described in the definition of pi exists in the truly flat space of our mental model of the circle’s environment. There the ratio of a circle’s circumference to its diameter is EXACTLY pi. Remember, circles, like lines, points, and equations don’t really exist in the physical world. They only exist in our minds. :-) ????
“Since Einstein, we’ve known that there is basically no such thing as “flat” Euclidean space-time.”
Except, of course, for like… the Universe?
https://en.wikipedia.org/wiki/Shape_of_the_universe
Even if that were the case (there is debate) – that would only handle a circle the size of the universe as a whole, local deviations are obviously a lot larger (Sag A). Near any mass – you don’t even need a singularity – pi isn’t the same as that neat formula that can calculate any digit of the irrational number it is (in flat space) you want. It’s a neat geometric construct with a lot of uses, and “close enough” as is – and since it’s been calculated to many more digits than matter on the earth (think you can’t measure resolution below Planck length) – which doesn’t have flat spacetime – ask anyone designing GPS birds – we use it, and not just for computing circle dimensions.
“Even if that were the case (there is debate)”
“There is debate”? It’s measured. Literally. The peak in the multipole spectrum of the CMB, combined with our knowledge of how far away the CMB is, gives you a triangle that you know all 3 sides of, and it indicates that the Universe, at that time, was flat to within 2%.
“pi isn’t the same as that neat formula that can calculate any digit of the irrational number it is (in flat space) ”
No. Pi *is* the irrational number. That’s what it is. By definition. The ratio of the circumference of a circle to its diameter in arbitrary geometry is not pi. In flat geometry, it’s pi, but on an arbitrary manifold you’ve got lots of nasty integrals involving the metric tensor. Those integrals drop away in flat space, but the actual formula for computing the amount of area enclosed by all points less than some distance “d” is what changes. Not pi.
Pi started off as the geometric definition, but that is *not* what it is in modern mathematics.
I actually agree with this – the real issue is the common use of pi as being defined as the ratio of circumference to diameter of circles, which only happens to be true in flat space time. I did read the linked wiki that, while it shows that _on average_ and only over the entire universe, ST seems flat to .4%. Scroll down only a little to see illustrations of huge local deviations from that – same article, and in this case “local” could be a galaxy cluster (or bigger), a bit bigger than any circle you’d likely want to characterize.
FWIW, even that article mentions that there is some debate and if you want to go to turtles all the way down, we could go with some assumptions about the CMB being redshifted electron-positron gammas and how various things might affect that shift even if the assumptions there and in anything like a Hubble constant are correct, but this isn’t the place for that(?).
Pi has a ton of other uses (I do Digital Signal processing and literally wrote a book on the topic) that have nothing to do with the happenstance definition above. This Quora thread has a decent take on that: https://www.quora.com/Does-the-value-of-%CF%80-change-relative-to-how-much-spacetime-is-warped
So the real issue is the original definition used in ancient times and carried forward incorrectly.
These guys have a cool channel that shows several geometric (and cool) pi definitions that have nothing to do with circles or the total degrees in a triangle in real space time. Fun!l
https://www.youtube.com/channel/UCYO_jab_esuFRV4b17AJtAw
“So the real issue is the original definition used in ancient times and carried forward incorrectly.”
Except it’s *not* carried forward incorrectly? Pi is not defined as the ratio of a circumference of a circle to the diameter in arbitrary geometry. It never has been. Not ever. It’s always been the ratio of a circumference of a circle to the diameter in Euclidean geometry.
And it doesn’t even matter if space isn’t perfectly Euclidean, because Euclidean geometry is a *mathematical* concept. Euclid starts with 5 axioms. If a space meets those, it’s Euclidean, and a circle in that geometry has C/d = pi. I mean, space isn’t perfectly *anything*, but that doesn’t mean we can’t use really, really good approximations to it.
The real mystery about Pi is what space time configuration we need for Indiana Pi. :)
if we leave time out of it, and just stick to the ‘space’ bit, then we can have good old-fashioned Euclidean geometry, where a circle is a circle and a square is a square.
I had some fun years ago looking for geometries that could apply to spaces in which pi was set at unusual values. Flat spaces could afford squares with 5 sides, or triangles with 3 right-angles. 3d geometries were less easy to visualise, but in one result I found that the connectivity of the platonic solids could be repeated for values of pi which are natural number multiples of the familiar 3.141…
It’s also worth remembering ,on this day when we have lost one of our greatest scientists, that those ideas can come from any type of person and that by embracing the diversity of human minds and bodies is so important if humanity is to reach its potential.
Yes, in the same sense that a given measure of carbon could be a diamond. The potential is there, but it requires the right circumstances and variables lining up to make it happen. Einstein could’ve been a watchmaker, and while he might have been the best damn watchmaker the world has ever seen, it would never make up for the lack of his theories.
Everyone *could* be a Galileo, Archimedes, or Sagan, the fact is that these people were outliers, exceptions to the grand majority.
Even among us, people with knowledge, passion, and drive to push the limits, only a small number of us will have a significant impact in the world.
That said, i do believe that we should all strive for greatness, but our expectations should be tempered by reality.
“The Monte Carlo technique is an inherently modern technique. It involves randomness, and it’s not a mistake this technique was discovered when attempting to find a solution to a problem involving probability and quantum mechanics. The ancients simply didn’t have the tools to discover this technique.”
Well… not really.
It actually doesn’t involve randomness. All you care about is that the dots you throw are equally distributed in the square. You could literally throw them completely deterministically, and it’d still work. It would just converge *slower* to the correct answer.
In fact, the reason no one did this is because, well… it’s a terrible way to do it. It’s really inefficient. You have to make a *ton* of trials in order to get a precise answer. Archimedes and the others in fact estimated pi *much* more efficiently than that. Archimedes did it by inscribing circles in increasing polygons. And by the 1500s-1600s, people realized that you could just use an infinite series to calculate pi (which is a *way* more efficient).
I also have no idea why people think the Monte Carlo way is cool. It’s a neat way to explain graphically how a Monte Carlo works, sure. But really, it’s the exact same thing as a direct measurement. Make a square of wood. Weigh it. Now cut a circle out of that wood with the same diameter as the side of the wood. Weigh that. Take the ratio, multiply by 4. Poof.
Now, the Leibniz formula for pi, *that’s* pretty cool. And obviously a much faster way for a computer to calculate pi, too.
Monte Carlo methods work very well for a lot of problems, but they tend not to be elementary problems. The area of a circle to the bounding square is about as good an elementary example as there is, though it is not one any rational person would use this method for.
Yes, the direct measurement of area/weight you mention is much quicker. Back in the day, before computers (or even electronic integrators), people would cut out then weigh the peaks from chart plotters to get the area under the curve for each peak.
@Pat is right about Monte Carlo.
For instance, you can solve any integral by adding up function values f(x) at random points, or you can pick them carefully and you’ll get a function that converges significantly faster: Simpson’s rule and other quadrature methods.
There’s a sub-type of MC called importance sampling where you pick the distribution to put more weight on the parts of the space that contribute more to the result. That’s halfway between “random” sampling (by which we mean uniform random) and picking the points directly. Consequently, it converges faster, but requires you to know something about the problem ahead of time.
Resorting to MC is like saying that you don’t know (or care) enough about the specifics of the problem to tailor a solution for it. That makes it a great general-purpose tool (like artificial neural nets) but it also means that there’s a better, specific solution that’s more efficient.
It’s a bad way to find pi if you’re serious about pi. But finding pi by MC is a great way to learn about MC methods.
Right. And the “don’t know or care enough” problem happens very often, and it can also be “can’t know” – as in, there’s no real way to know about all of the possible variations. If you consider things like a physics experiment, where you want to understand how a detector responds to incoming particles, you can build a Monte Carlo which is basically a complete physical simulator. Suppose you want to find out how many particles it can detect when they’re coming in from all directions: well, that’s an integral over solid angle. So you compute it via Monte Carlo by randomly choosing an incoming direction, and figuring out if it can be detected, and adding up all the cases where it can.
It’s a bit silly to call those “Monte Carlo simulations,” because sometimes doing it via Monte Carlo methods (random draws) is actually really stupid, and you’d be better off just stepping through one at a time with a fixed spacing. But the name stuck, so lots of simulations end up being called “Monte Carlo,” even though the real reason they’re so useful is because they’re a complete simulation.
Tau? Really? Hasn’t that died yet? Pi shows up in many, many places, such as the area of a circle for an elementary case, where tau would make for the same problem it is supposedly correcting.
Clearly you have not been exposed to more than the concept. In a lot of those many places it is multiplied by 2.
Your counter example is covered in the Tau Manifesto.
https://tauday.com/tau-manifesto#sec-quadratic_forms
Manifestos have no place in math. neither does the senseless arbitrary bickering about what symbol should have what value for what purely aesthetic reason. It is pointless and a waste of time.
I was not bickering, just pointing out that p’s objection shows ignorance about the thing being objected to.
I think the Tau people have some good points, and adding a new constant with a separate symbol will not cause confusion.
This is similar to the imperial vs metric argument, one exists because of history and the other because some people thought it was easier to use, but neither is wrong.
Some things in math are arbitrary and there is no one correct answer.
I wonder if Tau would also be considered racist.
Certainly a lot of people here consider π to be Euclideanist. I think we should be more inclusive and define π as “3, or maybe a little bit more.” By extension τ would be “6; good enough for government work.”
> if m.sqrt(x2 + y2) < 1.0:
Easy optimization: square both sides of the inequality, giving you:
if x2 + y2 < 1.0:
saving a function call is good in Python, and skipping sqrt is especially good. On my quick test, that led to a 20% speed improvement.
Are you sure?
https://www.wolframalpha.com/input/?i=(x%2By)%5E1%2F2+%3C+1.0
https://www.wolframalpha.com/input/?i=x%2By+%3C+1.0
they don’t have the same inequality plots…
That’s because you’ve plotted a different formula. In this case it’s x^2 + y^2 < 1 is equivalent to sqrt(x^2 + y^2) < sqrt(1).
But if you care about efficiency with numerical computations in python, numpy is where it's at – and runs about 12x faster on my computer.
from pylab import *
total = 1000000
sum(sum(rand(2, total)**2, 0) < 1) / N*4
Well, I used the two inequalities from the comment, sqrt(x2+y2) < 1.0 and x2+y2 < 1.0
x2 means x^2, i.e. sqrt(x^2+y^2). You plotted sqrt(x+y), and just ignored the 2.
How I Wish I Could Calculate Pi
3 . 1 4 1 5 9 2
(the number of letters in each word)
Ohh, I need a drink, alcoholic of course
3.1415926
Oh, that’s a great poem, I was just too lazy to Ggggle for it!
You guys really missed a good party back in ’15.
Started drinking early that day. Partied from 9 to 6.
Now I – even I – would celebrate
In rhymes unapt the great
Syracusan rivalled nevermore
Who in his wondrous lore
Passed on before
Left men his guidance
How to circles mensurate.
“A very slightly better way to celebrate…”
Nope! Nope! I’m gonna cut you off there, that is wrong!
July 22 is not good because that would be a day before month format and such a thing sucks.
No, this isn’t my side of the pond superiority complex talking either. Once you include year both sides got it wrong.
Year Month Day is the only order that makes any sense. Anything else is crap. It doesn’t sort right. Thanks for playing, Bu Bye now!
Yes, a Star Trek calendar I saw long ago listed stardates as yyyymmdd. And yes, it does sort easier!
Year, Month, Day will NOT sort properly soon. In less than 7982 years, all of your sorting algorithms will start producing wrong answers, and it will be the end of civilization as we know it.
Can you please run the code examples you publish through code review by a programmer of that language, before you publish them? At least read the style guide for the language in question (pep8 in this case) and/or run the code through a linter. Importing “random” as “dot” is a horrible idea. Calculating a square root of a number just to see if it’s larger or smaller than 1 is a ridiculous waste — you can compare the number directly for the same result. Mixing Python 2 (casting to float before division) with Python 3 (print as a function) is also confusing.broken? And what happened to syntax highlighting?
I think a Jupyter Notebook would be perfect for stuff like this.
I don’t think your reasoning for the multiplication by 4 is correct. If we’re calculating a ratio then it shouldn’t matter if we do it for a quarter or a full circle. The reason for the multiplication comes down to the ratio between the areas of a circle and a square.
Full circle/ full square
Pi*r^2 / (2r)^2 = pi/4
Quarter circle/ quarter square
Pi*r^2/4 / r^2 = pi/4
Thank you, I couldn’t for the life of me figure out how Total Point/Inside Point approximated pi. Inside Points/Total Points * 4 approximated Pi (as shown in the python code).
No problem. I was trying to work out the same thing when I realised this.
How about 355/113
I’m surprised nobody has yet mentioned that Archimedes was one of the first mathematicians to figure out how to work with numbers in the millions – The Sand Reckoner broke a lot of ground (or was that a lot of sand?) on dealing with numbers beyond 10,000.
Woohoo! I learned how to do Monte Carlo on a simple problem today! Thank You Brian.
There are only two acceptable families of date formats.
YYYY-MM-DD, YY-MM-DD, MM-DD — so Pi day is 03-14 or March 14th. too bad “-” is not a good radix point
DD.MM.YYYY, DD.MM — so Pi Day occurs on the 14th month? sorry nope. 27.09 is a reasonable approximation, but “/” would be better.
Obsolete European date formats like DD/MM/YYYY are not properly formatted. Check your ISO docs and the conventions used throughout Europe. You’ll find “-” or “.” in the forms I specified above.
US formats like MM-DD-YY seem weird and wrong. but at least 03-14-15 was the best Pi Day on US record.
finally someone commenting on the date :-) I agree, nobody sensible uses MM-DD – I’ve never seen it anywhere in the world apart from the USA, and even there it’s use is silly..
Especially when the ball dropped at 9:26 am.
“””That’s the jist of the above code, with one caveat; we don’t need to deal with negative x and y coordinates. We can simply ignore those, and multiply the ratio of the number of random points inside the circle over the total number of points by four.”””
You need to multiply by four whether you perform the simulation on one quadrant, or all four – the ratio is the same. The reason for having to multiply by four is because the ratio of the two shapes is: Asquare/Acircle = 4r2/pi r2. r2 cancels leaving Asquare/Acircle = 4/pi. pi = 4 x points in circle / points in square.
Replacing this code snippet still works:
# Place random dots in unit square
x = dot.random() * 2 – 1
y = dot.random() * 2 – 1
x2 = x**2
y2 = y**2
Maybe Archimedes only needed to count to a *quarter* of a million?
on the actual method above, while this isn’t a good way to find Pi, it is a good way to teach Monte Carlo simulation. My son did exactly this at school in grade 5, and them went on to using Monte Carlo simulation for other things.
Generally, people don’t realise how powerful this type of approach is, over the years I’ve used it to approximate solutions to things that are otherwise unsolvable… Particularly when it is now easy and cheap to plug a genuine (ie not pseudo) random number generator into the usb port…
Month/Day/Year makes perfect sense. There are 12 months of 28 to 31 days and an infinity of years. Lowest amount to largest. Day/Month/Year is the screwed up version, placing the smallest amount in the middle.
That format however places the most to least important to most people on a day to day basis. People are concerned when they wake up, what day it is (today is Wednesday the 14), what month it is (March), then what year it is (2018)? That also the order from changes most to least.
That’s the most insane explanation I’ve ever seen in defence of such a daft system.
Obviously, the number of variations within the three groups is immaterial to the arrangement of those groups. CCYY-MM-DD is the only perfectly logical arrangement if one is going to present the (century)year group in a sortable, meaningful order. DD-MM-CCYY is the reverse, but internally consistent. MM-DD-CCYY is nuts.
Regarding the sqrt() calculation efficiency in python…isn’t it correct to state that for any two numbers (x, y) > 0, if sum(x, y) <= 1 then sum(x^2, y^2) < 1; since the sum of the squares can only be equal to 1 if either x or y equals 0 and the other equals 1.
So presuming my assumption is correct, then wouldn't the most efficient test have been this
If x + y <= 1
and thus avoiding all the multiplication and sqrt() inefficiencies in the first place…but only because unit circles are being used of course.
(0.6,0.8)
0.6^2 + 0.8^2 = 0.36 + 0.64 = 1.0
0.6 + 0.8 = 1.4
Your example values violates my stated conditional
sum(x, y) <= 1
Your summation of squares equaling 1.4 doesn't disprove my initial statement.
Looking closer though, I see that the sum of squares must be less than 2 and not 1. This makes sense given the independent calls to random() guarantees that both x & y are less than one, thus x^2 + y^2 1.4 could have been generated.
What I think threw me, and possibly others too, is that the diagram suggests the points shown were based on the code. There is only a vague mention of not dealing with negative coordinates mentioned, but it is not stated why. There is also no mention that the center of the square/circle is (0, 0); thus the python code is ONLY creating dots for the upper right quadrant since random.random() returns values in range(0.0, 1.0).
Thus the picture shown should only have dots in the upper right quadrant and the * 4 code is a cheat to “simulate” negative coordinates in the other three quadrants shown. This seemingly violates the randomness assumed in a monte carlo estimate, at least imho.
@serpentheadz was correct that the ratio is all we need, but the * 4 in the code may not have been included for the circle/square area ratios listed, depending on the author’s intent relative to the negative coordinates vs the python code provided. But perhaps I’m wrong; the author did realize what @serpentheadz pointed out; the author didn’t explain it well; the further confused things with a drawing that didn’t reflect the output of their python code.
Mea culpa, there is a drawing showing just upper quadrant that I overlooked. Did not download to phone until refresh. Caption confirms my theory on * 4 “cheat” vs use due to ratios @serpentheadz called out. The full circle/square picture is still bogus.
Your formula will give you a diamond (square rotated by 45°) instead of a circle.
I wasn’t suggesting graphing my equation for a solution.
It was rather a question about the code logic for testing inner dots. I saw the flaw in my original suggestion and subsequent changes to underscore what seems poorly described in the article due to a misinterpretation of the original problem because certain details were only annotations on the diagram that didn’t download first time and article didn’t cover otherwise.
It must be a metric-to-imperial conversion problem.
I spent all day plaing with the code and watching how much more accurate it got over several iterations, averaging out the results each time….. no point, but I had fun – thank you!
Really? Someone is *still* on about Pi vs. Tau? I’m just going to leave this here: http://www.thepimanifesto.com
I was expecting that site to just be a big circle with “SUCK IT!” written in the middle.
If he could just count to 5000050000, he would have 4 decimals resolution and without any randomness.
import math as m
total = 100000.
# Points contained in the circle.
inside = 0
# Main loop
for i in range(0, int(total)):
x2 = float(i / total) ** 2
for j in range(i, int(total)):
y2 = float(j / total) ** 2
# Check if inside circle,
# increment counter if inside
if m.sqrt(x2 + y2) < 1.0:
inside += 1
# We're only doing positive x/y coords,
# so multiply by four.
pi = (float(inside * 2) / (total * total)) * 4
# Print result
print(pi)
# Print difference
difference = m.fabs(pi – m.pi)
print('{0:f}'.format(m.fabs(difference)))
Warning: it took 80min to run on my machine…
3.1416608264
difference: 0.000068
On Tau day what do you eat to celebrate it?
Taurus, of course (in other words, beef).
I might be up for the 6502 challenge… I calculated the prime numbers between 2 and 1000000 (one million) on a c64 with 64k.. And there’s 70000+ prime numbers in there.. Its all about compression :)
Here’s an acrticle on how I did it… I’ve since optimized it to take less than 40 seconds on a stock, real hardware c64.
http://www.technobabelfish.com/2014/07/calculating-primes-numbers-on-c64.html
github: https://github.com/garionphx/c64primes
Back on the day Martin Gardner presented the Buffon approximation “needle dropping* method in his Mathematical Games column. He then presented some pseudocode and challenged his readers to code it up on their personal computer (mine was an Apple ][+) and send him their results. He ended up with a few hundred π approximations aggregated over several million “needle drops”. He took the average of all the approximations. Most of us were limited by coding in BASIC with 8-bit floating point precision but, if memory serves, he ended up with the first 7 or 8 digits.