Cyclic redundancy codes (CRC) are a type of checksum commonly used to detect errors in data transmission. For instance, every Ethernet packet that brought you the web page you’re reading now carried with it a frame check sequence that was calculated using a CRC algorithm. Any corrupted packets that failed the check were discarded, and the missing data was detected and re-sent by higher-level protocols. While Ethernet uses a particularly common CRC, there are many, many different possibilities. When you’re reverse-engineering a protocol that contains a CRC, although it’s not intended as a security mechanism, it can throw a wrench in your plans. Luckily, if you know the right tool, you can figure it out from just a few sample messages.

A case in point was discussed recently on the hackaday.io Hack Chat, where [Thomas Flayols] came for help reverse engineering the protocol for some RFID tags used for race timing. Let’s have a look at the CRC, how it is commonly used, and how you can reverse-engineer a protocol that includes one, using [Thomas’] application as an example.

What’s a CRC, Anyway?

A CRC is a type of code designed to add redundancy to a message in such a way that many transmission errors can be detected. There are a number of different types of codes that can be used in this way, but the CRC has some properties that make it especially useful for communications protocols. First, it’s efficiently implemented in hardware or software. More importantly, it can be particularly good at detecting the kinds of errors often seen in common data channels, specifically, runs of bit errors. The simplest way to use a CRC is to apply the algorithm to the message to be sent, then append the resulting CRC value to the message. The receiver applies the same algorithm, then checks that the transmitted and locally calculated CRC values match. CRCs vary in length, with the most common ones being 8, 16, or 32-bits long.

Mathematically, a CRC is  based on division of polynomials over GF(2), the Galois Field of two elements. There’s a lot of interesting math involved, and a simple web search will turn up plenty of resources if you want to dive further into the subject. But, this is Hackaday, and I’m going to try to give you enough background to be able attack practical situations, so here we go.

In simple terms, the polynomials involved with the CRC algorithms have coefficients of only 0 or 1. There’s a simple mapping between binary strings and such polynomials, in which each set bit becomes a term with the bit position as the exponent. For example, the binary string 11011 can be represented as x⁴ + x³ + x + 1. (As a mnemonic device, think about x = 2.) To calculate an n-bit CRC, we append n zero bits to our message, then convert to a polynomial. We then divide this message polynomial by a generator polynomial specified as part of the CRC algorithm. The polynomial remainder of this division algorithm is the CRC.

Calculating CRCs

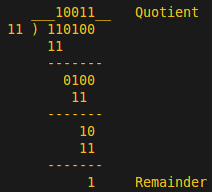OK, it’s going to get a little more relatable now. The division operation maps to a sequence of XOR operations that will remind you of basic arithmetic. For example, to calculate a trivial 2-bit CRC of the message string 1101 with the generator polynomial 11, we first append 00 to the message to get 110100, then divide to get a quotient of 10011 and a (2-bit) remainder of 01. This remainder is the CRC. Note that at each step of the long division, an XOR operation is used instead of the more familiar subtraction with borrowing.

This is all interesting if you want to write your own CRC implementation, but that’s probably not necessary; you can easily find implementations in your language of choice. If you do want to dig into the algorithms in more detail, here’s a good place to start.

Complications

Besides the generator polynomial, there are four other parameters that describe a general CRC algorithm. First, the input bytes may be reflected — swapped bit order from left to right. There may also be an initial starting value for the CRC calculation; this is prepended to the message before the division. After the division, the n-bit CRC may also be reflected, and finally, it may be XOR’d with a constant before use. While each of these steps is relatively trivial in itself, the resulting number of possible CRC algorithms is huge; too large for practical brute-force search for reverse engineering.

Reverse-engineering a CRC

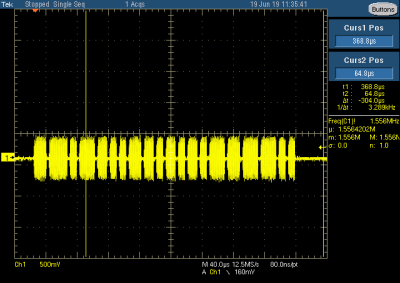
Remember [Thomas] and his RFID tags? After examining the RF-output of one of the tags on an oscilloscope, he made a simple receiver using a diode detector, RC filter, and a homebrew antenna. Connecting the receiver to an ESP32, he wrote some code to send back the received pulses to his computer for analysis. What he found was that each tag repeated the same 32-bit message about every 4 ms. Sixteen bits of the message were recognizable as the ID number which was printed on each tag, but the other half of each message was a mystery.

This kind of transmission is exactly why CRCs are used. Imagine if tag 5’s message suffered a bit flip during transmission and was received as tag 13. Adding a CRC allows this error to be detected, and the message discarded — a new one will be along soon enough. But, [Thomas], assuming the remaining sixteen bits of the message were a checksum, was now faced with determining which one. The first approach by the Hack Chat denizens was to try online calculators for common CRC types, but this didn’t yield results. While you might get lucky this way, checking the most common handful of CRC parameters, this method doesn’t scale. Luckily, there’s an efficient alternative.

CRC RevEng

A search for CRC reverse engineering turns up the right tool for the job. CRC RevEng by [Gregory Cook] was written to do exactly that: given a few examples of message/CRC pairs, it can determine the parameters of the CRC algorithm used. [Thomas] had collected the IDs and checksums from a number of tags, four of which are shown here:

5A2C DAFC
5B25 C378
5BBC 8B71
5C0A 3EEC

To execute the search, the reveng program is invoked with the ‘-s’ switch, and in this case, the known size of the CRC,  ‘-w 16’. Given just one sample, the program cannot determine which CRC generates the code:

With two samples, the program determines three sets of parameters which could possibly be used:

Finally, given three examples, the code narrows down the search to a single set of parameters.

From here, it’s relatively easy to verify that this set of parameters also reproduces the remainder of the 40 or so tags that [Thomas] has access to. With the CRC algorithm determined, he can now generate his own tags, or reliably receive data from existing ones.

It’s important to remember that the addition of a CRC code to these messages wasn’t intended to keep an adversary from faking the transmissions. As [Thomas] points out, since the tags are not synchronized in any way, their on-off-keying signals can easily collide and create receive errors. Checking the CRC on received messages provides some insurance against this possibility.

Spoofing CRCs

The CRC RevEng code can also manipulate a message to generate a desired CRC value, which can be useful for spoofing.  Called “reversing”, by the program, the behavior is invoked with the ‘-v’ switch. This usage requires that you can identify an n-bit section of the the message that you can change without negative effect – for instance, a comment field that is ignored. If you can locate such a contiguous space in the message,  you can substitute a value there to make any message have a given CRC code. This can be useful in spoofing packets that you need to change in some way, while maintaining a specific checksum value.

Wrapping Up

If you find yourself faced with some unknown data in a message protocol, consider the possibility that it might be a checksum. Although many RF protocols hide these values from users, if you’re looking at messages at the lowest levels, you may well find them. If you do, remember there’s a tool to figure out what’s going on.