Half the fun of getting vintage test equipment is getting to open it up. Maybe that’s even more than half of the fun. [CuriousMarc] got an HP 5061A Cesium clock, a somewhat famous instrument as the model that attempted to prove the theory of relativity. The reason? The clock was really the first that could easily be moved around, including being put on an airplane. You can watch the video below.
According to the video, you can simplify special relativity to saying that time slows down if you go fast — that is known as time dilation. General relativity indicates that time slows down with increasing gravity. Therefore, using airborne Cesium clocks, you could fly a clock in circles high up or fly at high speeds and check Einstein’s predictions.
 We really like the line from the device’s manual: “The Model 5061A Cesium Beam Frequency Standard is itself capable of defining frequency and therefore needs no calibration.” The definition of the hyperfine transitions of cesium was — by international agreement — 9,192,631,770 Hz.
We really like the line from the device’s manual: “The Model 5061A Cesium Beam Frequency Standard is itself capable of defining frequency and therefore needs no calibration.” The definition of the hyperfine transitions of cesium was — by international agreement — 9,192,631,770 Hz.
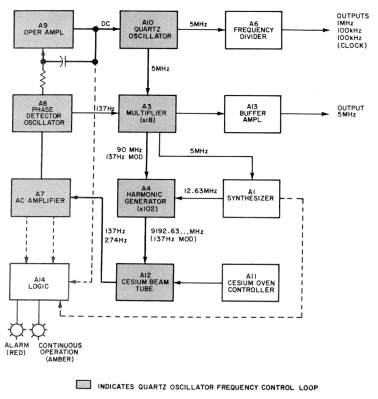
A 5 MHz crystal oscillator generates a signal that is modulated by a 137 Hz signal. The modulated signal gets multiplied by 18 and then, using harmonics, by 102. This provides a signal of roughly the correct value which excites the cesium beam tube. The tube’s output is used in a phase-locked loop to discipline the 5 MHz clock to be right on. This works because the tube will put out twice the modulated frequency if the carrier frequency is exactly the same as the cesium’s hyperfine transition frequency. If there is any variation, the output will include the fundamental frequency (137 Hz) which is absent if the loop is in lock.
The tube eventually runs out of cesium because the instrument literally boils away a few grams of cesium. [Marc’s] appeared to have some life still left in it. You can tell the instrument has been serviced because the tube is marked as Agilent, so it isn’t the original tube.
The video has a good explanation of cesium and exactly what hyperfine transition is. The defined frequency is in the absence of magnetic fields, but since the Earth has a magnetic field you have to have a strategy to deal with that. In the tube, there are strong magnets that overrule the Earth’s field. This cause an error, but a known error that the instrument can correct.
Ever wonder how clock standards were before the nuclear age? Most of us still have to settle for rubidium or GPS discipline.
















Did you enter this with speech recognition? It’s relativity!
Fixed. Well, I did misspell it and the spell checker, being helpful, changed it to what it thought was the right word. Modern technology.
g’damn 2.5k (GBP) on ebay
I see this historic masterpiece and then I see this CSAC thing and I’m just thinking, wtf?
https://www.microsemi.com/product-directory/embedded-clocks-frequency-references/5207-space-csac
Can I get it on Ali? 😁
Did you check all specs of the CSAC carefully? In a previous post here on hackaday ( https://hackaday.com/2016/09/25/rubidium-disciplined-real-time-clock/ ), [oneohm] comments that CSAC’s datasheet (presumably as of his writing, on Sept. 25, 2016) did not inspire confidence. The documents [oneohm] refers to in his comment can no longer be found on the Microsemi site! At a cursory look at the current data sheets (e.g. https://www.microsemi.com/document-portal/doc_download/133305-sa-45s-csac-datasheet) , I don’t see any yearly aging specs! In his comment, [oneohm] claimed it to be better than a crummy 1×10⁻⁸/year, but now in the CSAC datasheets I can only find a reference to a monthly aging of <9 × 10⁻¹⁰/month. Also, gone are the warnings about prolonged operation, mentioned in [oneohm]'s comments. There is a possibility that Microsemi may have improved the CSAC since then, but I suspect their CSAC is not all that great. Maybe somebody who has experience with it can chime in?
I think the difference between 10^-8/yr and 9*10^-10/month (12*9*10^-10 = 1,08*10^-8) is not that great.
Exactly, Martin! What I am saying is that along with the yearly aging specs (similar to the monthly aging specs listed today), the warnings about prolonged use of the CSAC, noted by [oneohm] in his comment in 2016, have also disappeared from the Microsemi web site. What I am wondering is whether Microsemi has improved the CSAC since when [oneohm] wrote his comment in 2016 or they are just playing a specmanship game. Because, as you remarked, the monthly aging they list today is about equivalent to the yearly aging they listed in 2016, I think they are playing a specmanship game. BTW, the CSAC was developed when that division of Microsemi was Symmetricom, if I am not mistaken.
> The tube eventually runs out of cesium because the instrument literally boils away a few grams of cesium.
So is the same true of a rubidium standard ? That the individual atoms migrate from one side of the other inside the physics package and never migrate back.
I had always ASSumed that because cesium has a low melting point of 28.5 °C and rubidium also has a relatively low melting point of 39.3 °C that any atoms that were accelerated from one side to the other was only temporary and that it eventually flowed back under gravity and was continuously recycled. But I guess that would not work in space.
No, but Rubidium has it’s own problems. With use, some of the Rubidium is deposited in the inside of the “lamp” and like an old incandescent globe, it dulls with age. The Rubidium bulb may be replaced or can often be brought back to life by removing it from the physics package and heating.
I think there is another difference between rubidium and caesium physics packages: Because in the caesium physics package the caesium atoms emerge from an oven, as described in the video above @10:17, the interrogating beam can be arranged to be normal to the velocity of the interrogated atoms. That can greatly reduce the Doppler shift (ideally zero when the interrogating beam propagates normally to the interrogated atoms) as compared to a rubidium physics package (where the interrogated atoms have velocities in random directions and gaussian-distributed magnitudes), which has a huge impact in the phase noise and Allan variance of the atomic process itself.
From back when HP made something besides junk computers and overpriced ink. Credit where credit is due, though – one of their network switches is allowing me to type this.
I have some old HP gear, and was even able to add a missing LO to my sweep generator because the manuals have enough information to allow you to build the missing PCB!
8590 spec analyser
a couple of bench DC power supplies
410C VTVM (might be functional)
Oh, and RPN forever! (HP-25 and HP-41)
The problem with HP is due to Carly Fiorina’s infinite wisdom of first splitting off the test and measurement division that made things like this (was Agilent and now Keysight) as well as the medical equipment, and then to make it even better decided that merging with one of the bottom 5 PC manufacturers was a good idea… Their industrial stuff is still pretty solid (servers, enterprise equipment, PCs like the EliteBooks etc) though…
The biggest thing is she thought she could do better than Bill and Dave…
I TOTALLY agree with you about this female jerk!! She did it first to Lucent and then HP. What a total waste of skin. Ruined a perfectly good company. Who ever sponsored her for the CEO job at HP anyway?
Caesium?
Yes, why not? It is a “normal alkaline metal”. Perhaps you think only of the infamous radioactive isotope which is generated in a nuclear reactor and sometimes liberated in an accident. But also one or more stable, naturally occuring isotopes exist.
If i had two of these clocks, and synchronized them, how long do they stay in sync? Indefinitely? What would happen if I put a lead shield around one of these clocks and not the other?
Excellent questions! To answer these and other similar questions, David Allan developed the Allan variance. It is similar to the variance taught in statistics classes, but is used when random processes are not ergodic. (In this case, the mean, the frequency of the oscillator, is not constant in time.) Wikipedia has a good description of the Allan variance: https://en.wikipedia.org/wiki/Allan_variance . The answer to your question is statistical (it has to be, given the randomness) and can be expressed in terms of the Allan variance. This is what instruments which measure the Allan variance actually do: They compare the frequency (e.g. zero crossings) of an oscillator under test, against a reference oscillator, presumed to be of higher stability. A question arises when the oscillator under test is expected to be as stable as the reference one. For this, the three-cornered hat method has been developed: http://www.wriley.com/3-CornHat.htm. To ease such calculations, the Python module ‘allantools’ has been developed: https://pypi.org/project/AllanTools/ . The Allan variance has an inverse relationship to the frequency away from the carrier in phase noise measurements, much like time and frequency in ordinary Fourier transforms.
You are also inadvertently asking another question, how to synchronize the two clocks. The Allan variance is useful here, too. Here is an example, going deeper than the discussion in the video above. When a quartz oscillator (frequently oven-stabilized) is disciplined, a PLL slaves it to a subharmonic of the disciplining process (atomic, or GPS). The control bandwidth of the slaving PLL (in radians/sec) is roughly the inverse of the time at which the Allan variances of the free-running quartz oscillator and the disciplining process intersect. Usuallly, the disciplining process has very crummy short-term Allan variance (=lots of phase noise away from the intended carrier, e.g. caused by the Doppler shift of random velocities of the molecules of the Rb gas), but low long-term Allan variance (=low phase noise close to the carrier). The opposite is true of the free-running quartz oscillator, so the two Allan variances intersect somewhere. That roughly indicates the time constant of the filter of the slaving PLL. See here for an example of such intersecting Allan variances defining the control bandwidth of the slaving PLL: https://www.thinksrs.com/downloads/pdfs/catalog/PRS10c.pdf (one page before the last). So, the slaving PLL decides what constitutes long-term stability (within the control bandwidth of the slaving PLL, phase noise at frequencies close to the intended carrier; stability relied upon the physics package or GPS) and short-term stability (phase noise at frequencies further away from the intended carrier, stability relied upon the quartz oscillator; outside the control bandwidth of the slaving PLL).
The effect of the lead shield would depend on the radiation environment and also the susceptibility of the system to radiation, I guess.
Sorry for not being able to give a more direct answer to your original question.
I know the frequency would be different if we used for instance, the Babylonian Second, but it’s always fun to see the number 137 pop up.
Old guy, that’s just numerology… :)