Randomness is a pursuit in a similar vein to metrology or time and frequency, in that inordinate quantities of effort can be expended in pursuit of its purest form. The Holy Grail is a source of completely unpredictable randomness, and the search for entropy so pure has taken experimenters into the sampling of lava lamps, noise sources, unpredictable timings of user actions in computer systems, and even into sampling radioactive decay. It’s a field that need not be expensive or difficult to work in, as [Henk Mulder] shows us with his 4-bit analogue random number generator.
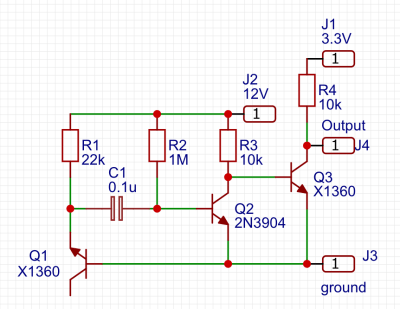One of the simplest circuits for generating random analogue noise involves a reverse biased diode in either Zener or avalanche breakdown, and it is a variation on this that he’s using. A reverse biased emitter junction of a transistor produces noise which is amplified by another transistor and then converted to a digital on-off stream of ones and zeroes by a third. Instead of a shift register to create his four bits he’s using four identical circuits, with no clock their outputs randomly change state at will.
A large part of his post is an examination of randomness and what makes a random source. He finds this source to be flawed because it has a bias towards logic one in its output, but we wonder whether the culprit might be the two-transistor circuit and its biasing rather than the noise itself. It also produces a sampling frequency of about 100 kbps, which is a little slow when sampling with he Teensy he’s using.
An understanding of random number generation is both a fascinating and important skill to have. We’ve featured so many RNGs over the years, here’s one powered by memes, and another by a fish tank.
I created a reversed biased transistor noise generator back in college in the 70s. It made a great source for gun, cannon, and other sounds with the appropriate analog filter post-processing, which was even more work. Back then, most of, if not all discrete transistors had lots of noise due to being made in those early years of silicon production before they had anything near to the level of sophisticated clean room environment that exists today for 12 nm geometries. Still, even then, the transistors had go through a candidate selection process as not all were equally bad, especially for semiconductor shot noise.
Agreed, in fact, I rejected a few zeners for lack of noise. This X1360 is probably a generic substitute for a generic NPN transistor that I ordered some time back. It has a 12V breakdown BE breakdown voltage that convenienty produces more noise than those with lower breakdown ratings.
The problem with these avalanche circuits (or at least those simple ones) is that it does not have flat spectrum. That sadly means that even though it IS random, you can make assumptions about its behaviour which lowers the entropy of the generated numbers.
Yes, that is what I found. There algorithms that can balance the one-sidedness but not the full distribution. I concluded that paradoxically for a smooth well balanced random spectrum you need artificial randomness. The only source of true randomness is probably quantum randomness but that’s more than I need.
> The only source of true randomness is probably quantum randomness
? How do you think electrons jump across the band gap from the valence band to the conduction band ?
“The only source of true randomness is probably quantum randomness but that’s more than I need.”
No, that’s really not true. I mean, you *are* using quantum randomness – where do you think the thermal noise that’s generating the breakdowns is coming from? In fact if you were using a reverse-biased Zener, that’s actually quantum tunneling.
The problem is that as with *any* true RNG, there are lots of other sources of noise and other timescales that get coupled in, and all of those alter the overall bandpass of the output, which means you have to postprocess it to flatten the spectral content. The postprocessing is by far the hardest part, far harder than finding an white source of entropy in the first place. Those are everywhere.
You are right, of course. The source of randomness is ultimately quantum possibly even stemming back from the early universe and it gets messed up as it works its way through an electron avalanche, exactly as you say.
I was more thinking of physical experiments such as the double slit experiment where the quantum function collapses randomly when measured and the single photons take one slit or the other.
“The source of randomness is ultimately quantum possibly even stemming back from the early universe”
Uh… no. You’ve got a bunch of electrons (producing a voltage) with an energy barrier (created by the doping) preventing them from moving to a lower energy state. Because you can’t confine those states purely, electrons will occasionally leak across the barrier due to tunneling, causing breakdown that’s measurable.
It’s a random state collapse just like any other quantum measurement, and if it had any memory of the early universe, it wouldn’t be random. When the breakdown happens is random – it has no memory of whether or not it’s broken down or when it broke down last.
It’s “pure” in a quantum sense because it’s not *possible* for it to have that memory because there’s no place to *store* any information.
“I was more thinking of physical experiments such as the double slit experiment where the quantum function collapses randomly when measured and the single photons take one slit or the other.”
The point of the double-slit experiment is that if you equally illuminate two slits and ensure that the incident wave propagates without interacting, they’ll interfere. If you instead alter it such that the incident wave has a chance of interacting in one or the other, it’ll start to destroy the interference pattern. If you alter it so much that the photon *always* interacts in one or the other, it’ll destroy it entirely.
But the “double slit” part has no randomness in it, it’s the detector part that does: you’ve got a beam of photons and two detectors, and you put the detectors at distances so they have an equal chance of detecting it. You don’t need a double slit to generate *that* kind of randomness, just use a single detector. Poof, exact same randomness. The question isn’t really what slit they go through. It’s whether or not their wavefunction collapses into one where it has interacted in the detector.
I was referring, as I’m sure you inferred, to the 1% of noise that is from microwave background radiation from the big bang that we find in all electric circuits. That is not a memory, or if it was, it would a memory of a random event.
Run a SHA-2 hash over the output to make it flat.
One key element is lacking. A clock function.
To resolved the issue.
Take the noisy analogue out, feed it to the micro’s ADC.
Take 32 samples, look only at the least significant bits, shift the 32 sampled bits into a uint_32 and voila. Not as fast, but pretty close to perfectly random.
The fact that bit zero over/under flows multiple times between samples ensures no bias to 1s or 0s. The fact that you string 32 after one another ensures no bias in the total number range.
That would be close to, if not completely random, in fact, I tried that and found that the ADC is significantly slower (as you pointed out) than the binary input. I use a Teensy 3.5 for binary sampling and the sampling loop acts as its own clock.
A clock would indeed be useful if you wanted to drive some logic circuitry like a shift register. A sample & hold would be faster than an ADC. One interesting question is: how fast should the clock be? If the shortest random spike is 1us, you could take 1 MHz. But that would create a signifcant bias for long sequences of 1’s and 0’s. If you make the clock too slow, i.e. 10 kHz you would almost certainly be undersampling and waste precious randomness.
I don’t actually know what the right answer is but have a gut feeling that there is no perfect point between under and oversampling for the simple reason that random bits and random and you can’t determine when you’re introducing bias in the random sequence because you can’t tell if the suquences are biased or not,,,
The clock function I am referring to is a mathematics function used in encryption, basically in c its mod. It is called a clock function because an analogue clock has 12 hours on the face, from 1 o clock you can add X hours to get to 2 o clock. X could be 1 hour, 13 hours, 25 hours etc etc. What was added is 1 + (X times 12) noone knows what X is. Basically let it roll over and you’re left with the remainder fraction. If you let the digit you are looking at roll over with a random rate of change, you will get a supply of random single digits.
Just googled that – fascinating stuff. Have to admit that I know vitually nothing about cryptography, I just about undersatnd PKI. I once struggled my way through hashing algorithms and can see how one could get into that but haven’t sofar.
My favourite source of relative randomness is the tiny camera you would usually find in an optical mouse. You can pick them up for a practically nothing, put them slightly out of focus and read off a value.
Or use a cheap webcam. Cover the lens, and turn up the gain until you get noise.
Those can be coerced to behave predictably, if you have a mildly radioactive substance or in fact anything else that’s known to trip CMOS sensors
I recall one project where a radioactive element from a smoke detector was added to a webcam to turn it into a RNG.
To solve this problem, simply don’t put a mildly radioactive substance near the webcam or anything else that’s known to trip CMOS sensors.
Either way, I’ve looked at some youtube videos on people doing that, and all that happens is the occasional random dot shows up. There’s nothing predictable about the exact location and pattern, so it just adds to the randomness.
For fun, I tried this with a webcam that I had lying around. Unfortunately, that model did not have very high gain, so there was only minimal noise. Leaving the lens uncovered and aiming it a small light worked much better.
“He finds this source to be flawed because it has a bias towards logic one in its output”
Biased random numbers can be transformed to unbiased trivially – von Neumann proposed a way back in 1951. Collect two bits, discard if identical, and transform 01/10 to 0 and 1 (whichever way you want). Poof, biased -> unbiased.
The real difficulty with RNGs is whether or not the bits are uncorrelated on all timescales, not whether they’re biased. Creating a real hardware RNG is basically the same thing as creating a precise clock, bizarrely – any outside fluctuations that couple in induce timescales and correlations, reducing the effectiveness of both.
Or use a schmitt XOR. Random to A input. Capacitor from B input to ground and resistor from Output to B input. Output then doesn’t have a long term bias.
Need a Random Number Generator?…
I defy anyone to prove, absolutely that radioactive decay is not a truly random phenomenon.
Furthermore…personal opinions and appeals to questionable authority–of any type–are, of course, dismissed out of hand.
********************************************************************************************
“The generation of random numbers is too important to be left to chance.”—Robert R. Coveyou
“Random numbers should not be generated with a method chosen at random.”—Donald Knuth
“Any one who considers arithmetical methods of producing random digits is, of course, living in a state of sin.”—John von Neumann
Decay is finite. Any given source will have a logarithmic decay, according to its measured half-life, gradually trending any randomness either smaller or longer, depending on what is measured. Further, while random, every isotope is statistically weighted towards stability or decay, affecting the rate of decay from fractions of a second to millions of years. Thus, there will be a systemic bias that must be corrected to be truly random over the range of the output.
Completely, utterly wrong. “Truly random” and “unbiased” have nothing to do with each other. Randomness is best thought of as Kolmogorov complexity, which in the case of quantum mechanical properties is, as far as we can tell, infinite.
“randomly change state at will”???
To improve your random number generator quality, XOR is your friend.
Just use two or more different random number generators, ideally with different technologies/methods. XOR the output of the RNGs together. The entropy of the result is the sum of the individual input entropies.
If you live in analog, use a diff-amp instead of the XOR.
Compression also improves things. Grab a FPGA, put the LZW compression algorithm on it, and “compress” your RNG output.
Instead of bothering with complicated LZW compression, just run it through a SHA256 hash. You’ll get better results with much less effort.
Our of interest can anyone explain why a slight bias towards 1s is bad. If you’re using random valeus for some cryptographic purpose in what way does it hurt if any bit has, say a 51% chance of being a 1 and a 49& chance of being a zero? Surely such a bias doesn’t let an attacker predict the next bit with much greater acuracy than if it were true 50-50 and the numbr of bits they want to predict overall means that even with the slight bias surely they don’t stand much betetr chance than with 50-50?? I’m sure I’m wrong but would like an explanation of why.
The author of this story doesn’t seem to understand that bias is not the same as non-randomness. Truly random events, such as avalanche noise and radioactive decay, are biased in that they do not have equal probabilities for 0 and 1 results. That in NO WAY means that they are not random. Elimination of bias is absolutely trivial unless the bias is so bad that you rarely see one result. The easiest algorithm to eliminate bias in this case would be to use the Von Neumann method: take two samples. If they are equal, discard them. If they are different and the first one is a 1, then the random bit is 1. If they are different and the first bit is a 0, then the random bit is 0. Voila! An unbiased source. Note that you CANNOT reuse either of the samples you discard if they are both equal.
The author requires a fair distribution and bias has a bad effect on that. That doesn’t mean that the samples aren’t random, they obviously are due to the nature of the noise source. Von Neumann may balance the distribution but it doesn’t flatten it. To the author, flat matters.
Intel came up with a neat randomness generator based on a ring of two inverters. They pull both the connection points high and then let them float. The state it drops into when the pullup transistors turn off is reasonably random and the generator can be implemented in the CMOS process usually used for digital circuits.
https://spectrum.ieee.org/computing/hardware/behind-intels-new-randomnumber-generator
I wonder if a discrete implementation of it would produce decent results. You could possibly use your existing circuits to add some more entropy/noise to the system.
In fact it would be interesting to couple all 4 noise source first stages directly to one set of gain stages.
I’m also curious how the output of your circuit might change if you added capacitive coupling between the 2nd and 3rd gain stages. Or maybe try a darlington pair or long tailed pair as gain stages.
Hmm, I may end up making some of these just to play with.
I might try that as well. It looks simple enough. I suspect that it will resemble any noise based number generator. The inverters are essentially high gain amplifiers. But I agree that the simplicity of the circuit is attractive. Rather than force the inputs up initially, I would switch the supply voltage off an on. That should create the same floating state.
You can get thousands of cross coupled inverters in a cheap SRAM chip.
An interesting experiment would be to take an SRAM chip, and write to it using an analog voltage about 50% between 0 and 1, and then read it back.
https://electronics.stackexchange.com/questions/248950/sram-isnt-blank-on-powerup-is-this-normal
This stackexchange refers to that initial randomness and shows interesting state diagrams with and without startup bias. https://electronics.stackexchange.com/questions/248950/sram-isnt-blank-on-powerup-is-this-normal
I’ve made VGA generators and they can show the power up state of a SRAM.
Some pics –
https://cdn.hackaday.io/images/6452151421901499460.jpg
and a higher resolution
https://cdn.hackaday.io/images/5356201421901322020.jpg
It may look random but it is lass random than it appears.
Noise during power up will create an element of randomness however there are also predictable behaviors in row and column addressing circuits.
What I did find though is that if you run a (10ns / 100MHz) SRAM faster than its rated speed and put your thumb on the chip then you would see random changes. This is just electrical noise using my body as an antenna and my thumb for capacitive coupling.
Even a Linear Feedback Shift Register (LFSR) would “look” random however a LFSR is probably one of the most predictable forms of PRNG.
The problem with random numbers that are algorithmically generated or conditioned is that they can be too random. Perhaps assuring that you don’t get two numbers the same within a certain time frame, would mean you could predict which numbers you won’t get by knowing which you’ve had before and thus gain an unfair advantage. Given enough samples, you could distinguish two seemingly random sequences. It’s like hiding from radar. If you’re too invisible then you stick out from the background noise instead of sticking out as an object.
The TV game show “Press Your Luck” could have saved a lot of money with this circuit back in the 80s. A contenstant learned their PRNG sequence and won hundreds of thousands of dollars.
No whammies, no whammies,, STOP!!!
There was no PRNG involved. The game designers used patterns and the contestant, Michael Larson, spotted and memorized the patterns.
Or use a better PRNG, with >= 256 bits of secret internal state.