It probably can’t have taken long after the first spectrum waterfall display was created, before somebody had a go at creating a waveform that would create an image in the waterfall. We don’t know who that pioneer was, but it’s over 20 years since Aphex Twin famously used the technique in their music, so it’s nothing new. If you fancy a go for yourself, [Gokberk Yaltirakli] has the project for you, creating waterfall images with an SDR from image files, using a bit of Python code.
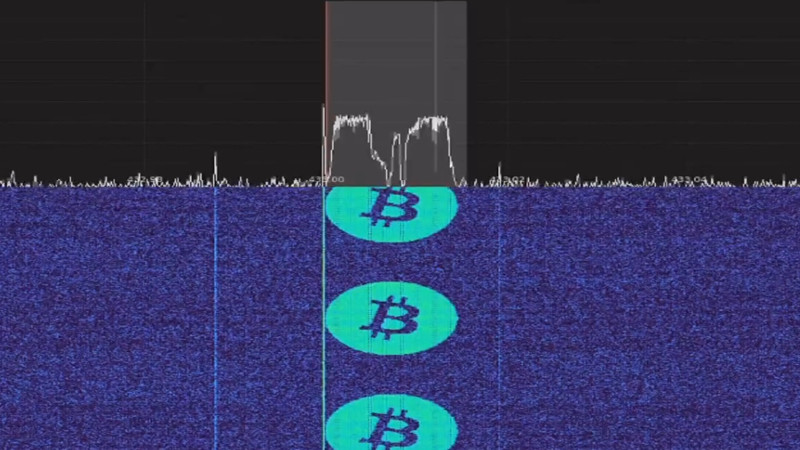
The value here isn’t necessarily in creating the waterfall of Bitcoin logos that can be seen in the video he’s put on the page, instead it’s in the simple explanation of creating I and Q values for an SDR. The code is a bit slow so writes its values to a file which is output by a HackRF, but it could just as easily be used by any other capable output device such as GNU Radio and a soundcard if you too want an Aphex Twin moment. The hardware for displaying a spectrum waterfall doesn’t even have to be very complex.
Thanks [Leo] for the tip.















Nice. Reminds me of the osc music: https://www.youtube.com/watch?v=qnL40CbuodU
I think first time I saw it was as a Winamp visualisation in ’97 or ’98. Don’t know it’s history before that.
Wait, neuron ran with a telegram from cold storage, miiiight have seen something similar in a late 80s 128k Spectrum Demo that was a response to, or inspired by something in the C64 demoscene, I remember a distinct, “If they can do it, we can do it” thing, but no idea if it was real time computed, a hacky way to get similar visuals without the same math, or what.
Anyone else remember a Ford TV ad from the mid 90’s with a brief 2 second clip of one at the end? I think it showed some text then switched to the Ford oval.
What old is new again?
https://en.wikipedia.org/wiki/Hellschreiber
Yeah, but Hellschreiber doesn’t do filled ovals! That’s kind of a neat trick.
Actually, now that I think about it for a minute, it’s trivially easy to put anything you want on a spectrum display: for every discrete frequency you want lit up, you generate a sine wave. You add these together, and modulate an SSB transmitter with it. Voila. You can do a full gray scale image (well, false color for most waterfall displays) this way, just by using different amplitudes of sine waves.
… what? Hellschreiber is basically (extremely) slow scan TV, with on/off pixels and an infinite field height. How does that have anything in common with “inverse fourier transform of input to feed to something else to take the forward fourier transform” ?
Oh, I see, you meant “C/MT Hell”, specifically.
Inverse fourier transform is MUCH simpler computationally than a fourier transform, as I explain in my comment above. You just have to add sine waves at the desired frequencies, at the desired amplitudes.
Untrue. The “inverse” fourier transform is mathematically the same as the forward fourier transform but with some gain adjustment. Both are nlogn usually, while synthesizing something with a bunch of sine oscillators is n². Everything depends on just what the constants are, though; for a small enough number of oscillators / frequencies it may well be faster to directly generate / detect the pitches directly without using the fourier transform.
Read what I said, not what you thought I meant. I said it was simpler. Not faster. And I may be wrong about “simpler” anyway. What it IS, though, is easier to understand, which to me means simpler. As for “computationally” simpler, it is, if you know from the start which frequencies you don’t even need to consider, which is the case here because we know how wide the bitmap is that we’re trying to display. In the special case of the object of this article, since a waterfall display is in frequency domain on the X axis but time domain on the Y axis, there’s only one dimension of transform we have to do.
But also, a discrete fourier transform is also n^2. You must be thinking of the FFT if you think it’s nlogn.
And then: “basically (extremely) slow scan TV”, you’re right. I forgot that Hellschreiber is in time domain troughout. It’s an easy mistake others and myself made, though, since it uses a waterfall display.
Would this be precise enough to encode .iso images?🤔
Mathematically it’s plenty precise, because you can calculate sine waves as precisely as you want, without limit. if you want to be able to modulate a carrier linearly enough to avoid any intermodulation, and receive it flatly and linearly enough to recover the original .iso file without error, that’s going to be another problem.
If you’re interested, this dude has been doing it well for a few years now.
https://gist.github.com/drmpeg/31a9a7dd6918856aeb60
Oops, wrong link. Here’s the code:
https://github.com/drmpeg/gr-paint