Electronics is really an applied branch of physics, so it isn’t surprising that if you are serious about your electronics, you probably know a little physics, too. If you’ve ever heard the term “fine structure constant” and weren’t entirely sure what it means, [Parth G] wants to explain it to you in about a minute. His video explanation appears below.
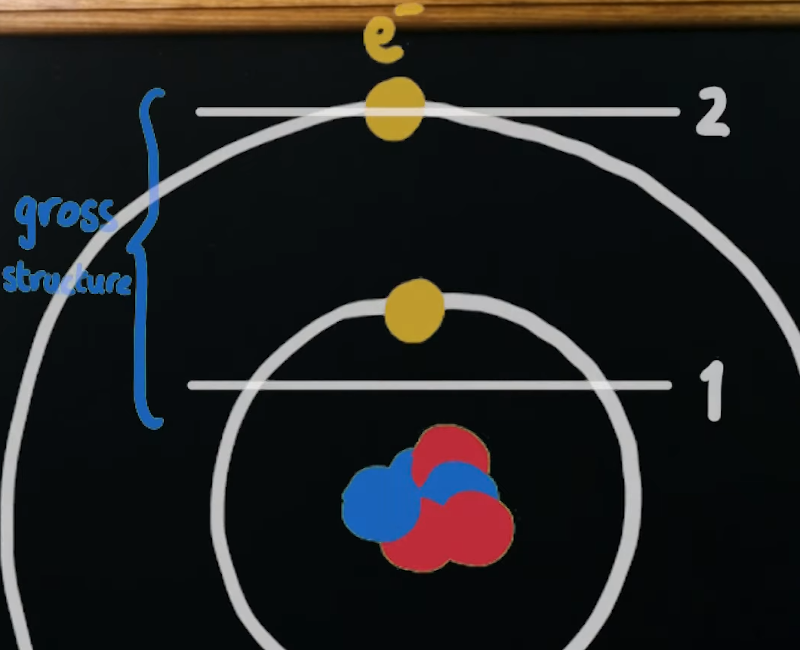
You may know that the constant, often represented by α, is approximately 1/137, but what does that mean? The answer relates to the orbit of electrons. You might remember from school that electrons orbit in shells around the nucleus. That is, an atom might have some electrons in the innermost shell, and more electrons in an outer shell.
As it turns out, if you look close enough, each of these shells is further divided into subshells, each with a discrete energy level. These subshells are the fine structure the constant refers to.
Each subshell is spaced a bit apart from the adjacent subshells in the same main shell. How far apart? The distance depends on the square of the product of the number of protons in the nucleus and — you guessed it — the fine structure constant.
Granted, maybe you need to know a little more about the fine structure constant, and that’s probably why the video is marked part one. But if you like little bite-sized chunks of physics, [Parth’s] channel has plenty including how to solve Schrödinger’s Equation and intuition about vector calculus operators. Typical of a physicist, [Parth] even tells us that Ohm’s law isn’t as simple as we think it is, although in real life, it almost always is.
We have a soft spot for people who can make physics more relatable. Or anyone, really, who wants to teach the true understanding of math and science instead of just rote formulae.
















This is my favorite expression for the Fine-Structure Constant, there are a handful of others. But as an EE my bias is showing. Let’s see if this will post intact in WP Jetpack, even without pre. It looks OK before posting:
α=(e^2*Zo)/(2*h)
Where:
α, Fine-Structure Constant, ~ 1/377 [dimensionless] [1];
e, Elementary Charge = 1.602176634×10−19 C [2];
Zo, Impedance of Free Space = 376.73031346177 Ω/cube [3];
h, Planck’s Constant = 6.62607015×10−34 J*s [4].
* References:
1. Fine-Structure Constant
https://en.wikipedia.org/wiki/Fine-structure_constant
2. Elementary Charge
https://en.wikipedia.org/wiki/Elementary_charge
3. Impedance of Free Space
https://en.wikipedia.org/wiki/Impedance_of_free_space
4. Planck’s Constant
https://en.wikipedia.org/wiki/Planck_constant
From a fundamental standpoint, it’s really nicely communicated as the square root of the ratio of the potential energy of ground state hydrogen and the rest mass of the electron.
If you imagine a ludicrously classical model of the hydrogen atom, alpha is the fraction of the speed of light that the electron is orbiting at.
The reason it’s nice (even though it’s obvious nonsense) is that the fine structure constant is actually the electromagnetic coupling constant, and the fact that it’s “less than one” is super important – it’s what makes it a long-range force. A coupling constant of greater than one can only be a short-range force.
Why? Well, again, think of the “simple model” – alpha greater than 1 would mean greater than the speed of light. (In a less nonsensical model, the PE in it’s ground state would be *greater* than it’s rest mass – trying to rip it out would just make another particle).
This allows you to understand a “coupling constant” for any force: ratio of potential energy to rest mass for a bound particle.
“It looks OK before posting” > And looks OK after posting. I’m surprised.
You have alpha = 1/377 vice 1/137. Dose not look right to me. What am I missing?
In the above article, alpha is approximatly 1/137 but you have here in your list 1/377. If it is dimensionless, one has to be wrong. Seems like it should be 1/137 if I remember right.
I feel stupid for asking, but does it make any sense to explain the fine structure constant like this? Saying that a quantity is proportional to a constant means nothing to me…
The FSC is an unsolved problem in physics up to now. From a theoretical point of view. Pauli (Sommerfelds student) was looking for a principle theory to come up with the FSC number. All the physicists since Sommerfeld defined the constant in 1916 failed to solve this problem. Why? I think all are believing the solution is hidden within QED. It is not. Why? Otherwise Pauli and his colleagues had done the job already. So I believe the solution is hidden within General Relativity. But you need to combine the principles from GR to be combined with those from Thermodynamics. Steven Hawking could have done it. But he did not. why? Keep on tracking.
http://www.totemconsulting.ca/FineStructure.html
Alfred Simpson