[Ihsan Kehribar] points out a clever trick you can use to quickly and efficiently compute the logarithm of a 32-bit integer. The technique relies on the CLZ instruction which counts the number of leading zeros in a machine word and is available in many modern processors. Typical algorithms used to compute logarithms are not quick and have a variable execution time depending on the input value. The technique [Ihsan] is using is both fast and has a constant run time.
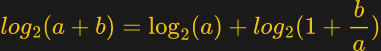
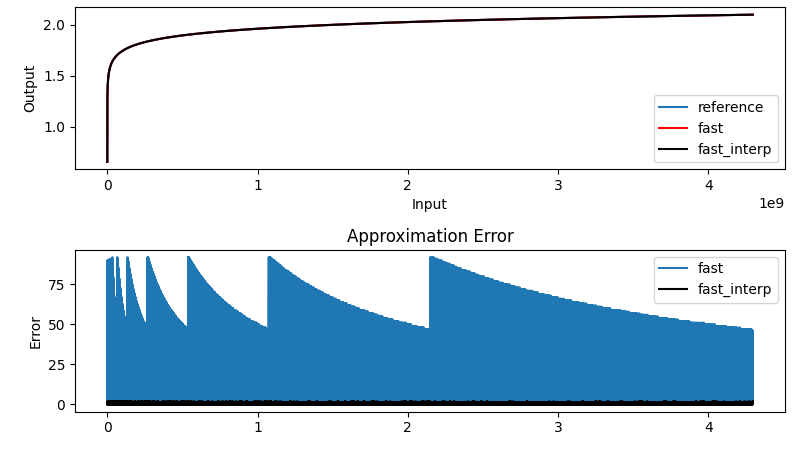
The above equation summarized the math behind the algorithm. We get the first term easily using the CLZ instruction. Using the remainder and a pre-computed lookup table, it is possible to get the second term to various degrees of accuracy, depending on how big you make the table and whether or not you take the performance hit of interpolation or not — those of a certain age will no likely groan at the memory of doing interpolation by hand from logarithm tables in high school math class. [Ihsan] has posted an MIT-licensed implementation of this technique in his GitHub repository, which includes both the C-language algorithm and Python tools to generate the lookup table and evaluate the errors.
Why would you do this? Our first thought was real-time streaming DSP operations, where you want fast and deterministic calculations, and [Ihsan]’s specifically calls out embedded audio processing as one class of such applications. And he should know, after all, since he developed a MIDI capable polyphonic FM synthesizer on a Cortex M0 that we covered way back in 2015.















CLZ is very interesting. I can think of a few algorithms where your result is a 1-hot word with position of the bit being what you’re interested in.
I doubt if many compilers emit a CLZ for the various ways people wrap up those algorithms.
on an M4/M7 with fpu won’t VCVT.S32.F32 do most of it in one go?, exponent and mantissa
If you want a hardware version, I created one ~15y ago…
https://www.edn.com/single-cycle-logarithms-antilogs/
Also on OpenCores.
Wow. That’s cool. Speaking of hardware implementations, there are analog logarithmic amplifiers, but they can suffer from dynamic range, accuracy, and bandwidth issues.
Still useful.
https://youtu.be/IgF3OX8nT0w
When memory is scarce, or more precision is required, one can use the remainder (xremainder_big in the code) to compute a polynomial approximation of log2(1+remainder). So it is possible to tune the accuracy with the order. In its simplest form (order 1), a shifted xremainder_big will do the job. The advantage of polynomial interpolation over simple lookup (fast_interp) is the function continuity, instead of staircases.
And yeah, fast log2, exp2 and sin/cos approximations are the bread and butter of audio DSP!
” those of a certain age will no likely groan at the memory of doing interpolation by hand from logarithm tables in high school math class.”
Big blue book
https://store.doverpublications.com/0486612724.html
Kudos for bringing up NIST’s Abramowitz and Stegun. I discovered a few years ago that their classic book is available free as a PDF. According to Wikipedia,
“Because the Handbook is the work of U.S. federal government employees acting in their official capacity, it is not protected by copyright in the United States.”
What’s curious is that regarding a NIST follow-on digital edition in 2010, presumably also prepared by “federal government employees acting in their official capacity”, Wikipedia says that this edition is covered under copyright by NIST. Hmmmmm…
Lots of bit twiddling algorithms including logarithms
https://graphics.stanford.edu/~seander/bithacks.html
RichC, interesting, the author of that website you linked to offers a $10 bounty if you can find any bugs in his algorithms. I wonder if he’s had to make any payouts.
I did exactly that many years ago when writing assembly code for Texas Instruments TMS320VC55XX low power fixed point DSPs. But instead of CLZ (that is not available on those chips IIRC), I used the really handy MANT::NEXP instruction, that in 1 cycle computes the mantissa and exponent of the accumulator (being the exponent 8 – the_number_of_leading_zeros: https://www.yumpu.com/en/document/read/6854217/tms320c55x-dsp-mnemonic-instruction-set-texas-instruments/287). Coding in assembly language for those DSPs was really fun!
The way I would had done it;
Have a table of log2(x), of each prime number, from 0 to 256.
since log2(x * y) = log2(x) + log2(y), all you have to do is perform a prime number factorization, which of course is very easy and trivial. There are many other articles on hackaday on how to do fast prime factorization, how to break RSA-65536 keys, and the cellphone number of santa claus.
So anyways, if the number is a prime number above 256, you could try and check the value for log2(x-1) and log2(x+1), and do some interpolation. Thats if the numbers nexts to x can be factored with your list of prime numbers.
What the current post describes, is using this same method, but with a short log table [ log2(2) = 1 ].
what CLZ is doing is factorying how many times do you need to multiple 2 in order to get that number.
Imagine having this log2(x) table;
log2(2) = 1
log2(3) = 1.58496250072
log2(5) = 2.32192809489
log2(7) = 2.80735492206
If I want to know the result of log2(35), I would break that 35 and get its prime factors;
5 x 7
then peform a lookup for;
log2(5) + log2(7) =
2.32192809489 + 2.80735492206
5.12928301695 = log2(35)
now, if I want to know the result of log2(11), I would have to interpolate the result of log2(10) + log2(12) since 11 cannot be factorized using my previous short table;
log2(10) = log2(2) + log2(5) = 1 + 2.32192809489 = 3.32192809489
log2(12) = log2(2) + log2(2) + log2(3) = 1 + 1 + 1.58496250072 = 3.58496250072
avg(3.32192809489,3.58496250072) = 3.453445297805
which is close enough (2 decimals) to the real answer; log2(11) = 3.45943161864
Factorization is definitely not “fast and easy” and doesn’t run in constant time. Which was a goal of this algorithm.
Of course factorization is not trivial. Even if we convert those prime numbers to their log2(x) reprentation, you would still need to solve the Knapsack problem
https://en.wikipedia.org/wiki/Knapsack_problem