If you mostly deal with DC current, you might not think much of root mean square or RMS measurements. Sure, you’ve seen meters that have “true RMS” settings, but what does it mean? If you don’t know — or you want a refresher — watch [Prof MAD’s] recent video explaining the topic.
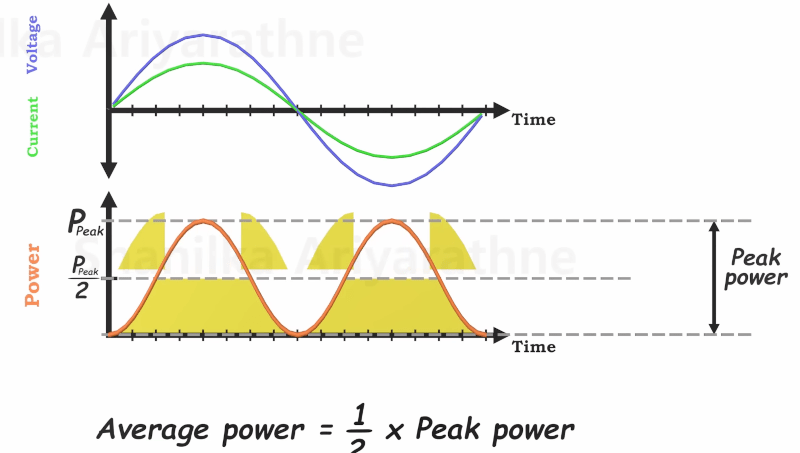
There are two things to remember when working with RMS. If you put, say, 100VDC through a 100-ohm resistor, you’ll draw 1A and use 100W of power. However, since AC gradually makes its way to a peak value and then starts ramping down immediately, you can’t use the peak value or anything like it to figure out AC power. After all, the voltage is only at that peak for an instant. That’s where RMS comes in. 100 VAC RMS through a 100-ohm resistor will also consume an average of 100W over time.
The other thing to remember is that we use shortcuts for sine waves where we take the peak voltage and divide by the square root of 2. That only works for sine waves. For anything else, you need either hairy math or some way to directly measure the power.
RMS is one of those details a lot of people miss so we’ve seen other explanations for it. If you want to derive the math for an arbitrarily complex AC waveform, you are probably going to need some calculus.
















I was taught that RMS is the voltage / current which will heat a resistor to the same amount as a DC voltage.
And yes, they also taught that it was the SQRT of 2 for pure sine waves.
I was taught that RMS always stands for Richard M Stallman, our GNU savior
I always wondered what RMS titanic stood for, before i heard of either of those terms, turns out it’s Royal Mail Ship.
Fact of the day, ty sir!
There’s an RMS (Stallman) Titanic / Hurd joke in there somewhere…
Well, yes. 100 VAC RMS through a 100 ohm resistor consumes an overall average of 100 watts, dissipated as heat. 100 VDS through a 100 ohm resistor will do the same thing – consume 100 watts and dissipate it as heat. Two ways of saying the same thing.
And both are wrong if we are picking nits.
Volts don’t go through anything. Voltage is an electromotive force applies between two points.
its also two times the sine of 45 degrees. one for each half of the wave and 45 degrees is half way between horizontal and vertical, rotationally speaking. makes perfect sense if you know your trig.
It’s not that difficult.
When you’re measuring a signal, you take each sampled value and square it. That’s a handy way of getting the absolute value, because two negative values multiplied becomes a positive value. Then you take the average, which is to say the mean of your squared sample values over some time, and take the square root of that.
In other words, the RMS value of a set of values is the square root of the arithmetic mean of the squares of the values.
It’s basically just flipping the negative half of your AC signal to be positive, and taking the average value of that. The reason why it has to be squared before you take the average is that your signal power to some load R is proportional to the square of the amplitude: P = V^2 / R so finding the same effective DC value requires you to find the average V^2 instead of the average V.
Right.
Kepp in mind that you need at least 8 periods of the lowest frequency sine wave in the signal for this to work.
This is the reason that most true RMS voltmeters specify a low frequency limit for the RMS readings. They use a fixed time period to sum up the RMS. The low frequency limit is where there’s no longer enough complete waves of the signal within the integration period to meet the needed accuracy.
I went through the math of it some time back. If I remember correctly, you need 8 full waves to get 1 percent accuracy.
Depends on what exactly you’re trying to measure. You can calculate the RMS value of a single cycle, and sure enough that’s what you’ll have.
The question is, what is the meaning of such values. Are you trying to measure the statistical mean amplitude of your AC source, or something else?
The ironic bit is that there are no longer light bulbs with a resistance R, since incandescent bulbs of all types are banned, so the example in the video does not apply.
In reality, in a light bulb there is a diode with a threshold voltage of about 30 volts, and a constant current device that limits the current to some few milliamps, so the power actually switches on and off every AC cycle. In a 230 Volt system the duty cycle is something like 96% and the power is directly proportional to the voltage since the current is constant above 30 Volts.
More modern LED bulbs keep the input power constant using high frequency switching ballasts, so the basic current waveform becomes the second harmonic frequency of the line frequency, again with a hard cut-off below 30 volts or so and a dip at the peak voltage. It has better energy efficiency in terms of the LED and its ballast, but a terrible power factor which results in power quality problems elsewhere in the system and heating up distribution transformers outside of the home. The nasty non-linear switching and high harmonic content of the current waveform causes cross-talk between conductors and things like ground fault interrupters no longer work properly.
There is a typo on the second slide titled “Root mean Squre” instead of “Root mean Square”
Incandescent bulbs are still with us, and will still be for a long time, as manufacturers have a serious plant investment in them. In the US, only 60 watt household lamps were outlawed by the Obama administration, and IIRC, that order was rescinded by trump. The stores are still full of incandescent lamps.
I could believe some of the other stuff, but are you arguing that the switching supply for a normal home’s lighting is big enough to harm a pole transformer by overheating it? I can’t imagine how that wouldn’t require either a ridiculous quantity of light bulbs per house or a ridiculously awful power supply. The modern efficient bulbs should be 4 to 8 watts of real power per bulb unlike older and cheaper ones. It seems like to magnify that average by enough to go beyond the transformer’s rating even for a tiny fraction of each second, they’d need to in perfect synchronicity consume all of their average in a few microseconds of a near-short-circuit each half cycle or something.
The RMS value of a signal is only properly understood by using the defining equation
https://en.wikipedia.org/wiki/Root_mean_square
Yeah but deeply understanding an equation is often a visual thing.
Radians, sin, cos, tan mean a whole lot more when you see them visually. It then becomes really clear why trigonometry is used to calculate their relationships rather than just some formulas to remember.
https://betterexplained.com/articles/intuitive-trigonometry/
To see it in action on audio, fire up Audacity. Set the meters from default shady to RMS, two holding peaks, normal, and RMS is the lowest color on the display. RMS is the power needed to drive speakers and heats up things. Lots of peaks may sound loud but don’t consume much power.
I’ve been acquainted with RMS, but perhaps we should send this video to the sellers of about twenty thousand various speakers and audio amplifiers on Amazon and eBay…
Like bailing the ocean.