If you had the traditional engineering education, you’ve made your peace with calculus. If you haven’t, you may have learned it on your own, but for many people, calculus has a reputation for being super difficult. While some of the details can be very tricky, the core concepts are actually simple and [Mathologer] has a very simple explanation along with some good graphics that can help you get started on calculus mastery if you’ve been putting it off. Using a car on the highway as the prototypical example, he covers quite a bit of ground in the 30 minute video that you can see below.
Of course, this isn’t a unique idea that calculus is actually simple. The video credits the great book “Calculus Made Easy” that we’ve talked about before. That 100-year-old (and then some) book has a similar approach to the topic.
Unlike a lot of similar videos, this one covers more complex things like various rules and the integral and derivative of trig functions and logarithms. It presents them in a colorful graphic that might be easier to digest than a dry table.
Of course, tying your shoes and algebra are also easy unless you don’t know how to do them. But it is funny how many students struggle with the subject when it is possible to have a straightforward intuitive understanding of it very quickly.
Do you remember the scene in “Something About Mary” where the hitchhiker becomes upset that his “7 minute abs” video might be displaced by “6 minute abs?” If that resonates with you, you could try this decidedly less tranquil video that purports to teach calculus in 20 minutes. We’ve even done our own attempt at making it easy.

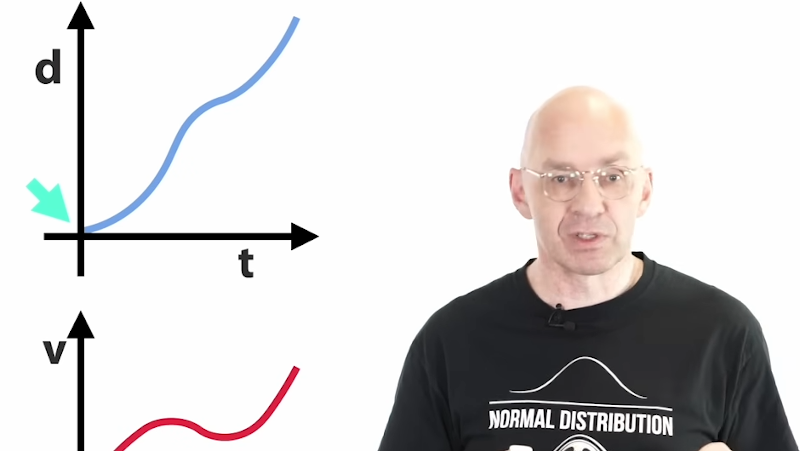














Any explanation that just has graphs and formulae and a presenter who recollects how easy it was for them at age 14 to grok calculus is IMO NOT the “easy” way for beginners to understand it.
I think a visual, working mechanical demonstration gives a much better understanding (where the accompanying graphs are supporting) and to that end I think this video is a far better one:
The Mechanical Integrator – a machine that does calculus
https://www.youtube.com/watch?v=s-y_lnzWQjk
Of all the calculus videos on YT, for me this is *the* one I would show students in a mathematics class.
I really like Mathologer’s work (along with redpenblackpen and 3blue 1brown and Zack Star and Tibees) but this video falls short. I think he just knows the material too well. It went too fast and skipped too much and was weak in the wrong places. I taught high school math and AP physics for 5 years and am willing to guess that even the very interested new calculus students do not have solid enough algebra and trig to get much from this video before they are lost.
There is an intimidation and expectation barrier caused by the names and the ‘mystery’ surrounding calculus and differential equations and real analysis and abstract, etc. I have often wondered if it is easier to learn arithmetic. Then arithmetic with variables (algebra) and arithmetic with variables that change (calculus) and with variables that change in more than one direction at the same time (multi-variat) and with variables who’s RATE of change is important (DEQ), etc. and leave out these descriptors. If one continues in math eventually they come full circle and define algebras over a tangent space with operators that follow certain rules and all that, and what we call arithmetic pops out as a special case.
“3blue 1brown ” uses too much colors, it’s distracting and often hard to decode, and his visualizations are overloaded.
I’ll have to checkout redpenblackpen.
Nice, although a white dot in the center of that integrator disk would give a visual point for the overlays.
Calculus is no big deal. Why do so many people get worked up over it?
Just cut through all the sugar coated rubbish and find somebody to give it to your straight (i.e. uncut).
Because they flunked it, repeatedly.
This. I flunked calc 1 twice before somebody explained to me, in simple words and concepts, what the heck calculus was actually for and how it worked. After that, straight A’s through 20+ credits of calculus and physics.
You mean cut, so the fluff gets removed that is really distracting.
What however is complicated is several applications of calculus that go beyond the trivial introductry examples.
Partial differential equations for example or other complex applications in physics or electronics, because of the many abbreviated calculations. But they rarely expand on the relevant parts, and instead add uslese “real” life analogies.
Intuitive understanding is not reached by making it colorful or “pretty” or relating it to social interactions. It’s by explaining the relationships and the steps in the most simple way, not the most abstract, but most simple.
Dear Al, I really appreciate this– For my own sake, I always struggled with it because during my junior year in high school I was suddenly shifted of to Munich because of parental choices, signed up for the IB system, as Jenny must be more familiar, enrolled in the IB system.
I am certain I am not Gauss, but I totally tried to ‘jump’, missing a semester of something.
Though the education there was *excellent*, I basically went from Algebra I, to AP Calculus, and skipped/missed something, and thus struggled.
It has always been, of mine, a deep and humbling regret, and, in a pinch, am rather glad others managed CAS, or– oh my ‘Wolfram Alpha’.
Yet, though subjects themselves may never change, we can (always) learn to be better instructors of them.
That is a fact which is always ‘game’.
Or as the quote from the title page of the new von Neumann biography I am finally finishing:
“If people do not believe mathematics is simple, it is only because they don’t realize how complicated life is.”
Subjects may never change, but teachers can, and should.
“Subjects may never change, but teachers can, and should.”
I feel that’s a life lesson in general. Experiences, insights, (emotional) meaning, growth in general should not be too attached to specific people.
Calc comes easier to some, harder to others. Learning anything in a particular way (visual, tables, abstract, word problem..) comes easier to some than others. After I dedicated several hours a day for a year or so to calculus, it was super easy. But hey, maybe someone can do it in 30 minutes. I’m sure English composition can be made easy in 30 minutes, too, start banging out the next Great American Novel after an episode of The Simpsons.
Become a HaD writer.
Agreed
My roommate in college could do calc like a breeze but I struggled with it. Consequently I could easily understand and do discrete math whereas he could not.
Now I need a video on “Algebraic Topology is … Easy” or “Quantum Field Theory is … Easy”
Well, it is all algebra. Or one should say, algebras. By the way, check Clifford Algebra and Geometric Calculus if you want to see those things get simpler.
I haven’t looked at the graphics yes, but “colorful graphics” always makes me uncomfortable. First of all, people rarely ever chose colors for color vision deficiency, so it’s a stressing guessing game of what means what, and thereby increasing the cognitive load instead of decreasing it.
Also it’s people who prefer to use countless colors, which is actually *worse* than “dry” symbolic or graphical representations. It’s like people who use bold text all the time, it’s distracting.
I find those people don’t think enough about alternative representations and rely on color too much, where it is well known that it is important to encode information redundantly in different ways (while trying to keep it visually simple) to make it the most accessible and easy to learn.
In short: color is not the answer to problems of understanding, often it makes it WORSE.
I agree – colour coding is not auitable of all. I hate it when someone reviews a document and marks the changes in red. For me, the difference between black text and red text is the difference between black text and very very dark grey text. So glad when I found that Word could search/replace on text formatting and colour.
I agree, things should be presented simply, adding colours gives it the veneer of simplicity. Presenting graphics in black and white impose limitations that force people to make them truly simple and understandable.
Stick with Sylvanus P Thompson then, no color illustrations.
Color is fine, just not overuse of it. The balance and contrast matters, and that it is one of many modalities to encode information.
The problem I had with advanced maths was that different teachers / lecturers / books would use different symbols and each presentation was riddled with errors. I always craved ‘proof’ and real world applications and standard symbols. If I have any math probs these days I hard code them in Python / C++ to understand what is going on and prove that they work with Matplotlib graphs or whatever.
This channel is for you. https://www.youtube.com/watch?v=1yBPEPhq54M
The main problem I had with advanced maths was that diff teachers / lecturers / books would use diff symbols and each presentation was riddled with errors. I always craved ‘proof’ and real world applications & standard symbols. If I have any math probs these days I hard code them in Python / C++ to understand what’s going on & prove that they work with Matplotlib graphs or whatever.
That actually makes a lot of sense. Similar to how programming something yourself helps you to understand better. It’s one of the cases where “reinventing” the wheel is actually benefical.