A hard drive crash, and some other happenings that aren’t entirely clear to us, led [Devbisme] to put in a parts order. As he wanted to make the most of his shipping costs, he decided to fill out the order with parts that he’ll use eventually. He’s been working with surface mount designs and wanted to move from using resistors with 0805 packages to the 0603. Having nothing on hand, he devised a way to account for almost all standard values with the fewest number of different resistors.
That’s a mouthful, but what he actually did was figure out what combinations of resistors can best be wired in parallel to achieve a different standard resistance value. This way, if he doesn’t have a specific value he can solder one 0603 surface mount resistor on top of another one to get there. He ended up writing a Python program to best calculate this set of values. It came up with a set that lets him synthesize 159 of the 168 standard resistor values within +/- 4% using just 19 actual resistor values. His method requires anywhere from one to three resistors to get to each value. Soldering three 0603 packages on top of each other might not be the most fun, but it makes for easy parts inventory management.
















I guess you didn’t read the article all the way through. He concluded that it comes cheaper to just buy a kit for $40 then to waste time with stacking.
Reread it, he would have saved money, but not enough to justify the effort involved.
However, one like myself finds this incredibly easy, I only ever work on small projects, requiring a few resistors. There’s no easy way to get just one resistor of the value I need, this is a much more viable option as I have 100s of resistors of random values sitting around not being used.
What I’d like is an app that takes in a number of known resistor values (exact as measured) and attempts to combine them in some fashion to get a target resistance.
Ex: I have 4 different resistors, what combination leads to the closest target resistance?
Wolfram|Alpha can sort of do the reverse. Search for a resistance (35 ohms, for example), and it will give you various networks using standard values that will get to that.
http://www.wolframalpha.com/input/?i=35+ohms
Nice. I used Wolfram|Alpha for a couple of nifty numeric searches before, but definitely didn’t realize it would auto-calculate resistor networks.
Oh snap, that’s close enough.
As if I didn’t use Wolfram|Alpha enough as it was.
I have used this technique, but from a backwards perspective; stacking or adding components to match the requirements from a limited supply. You can put them in series by making an inverted ‘V’ with them on the board. Can be done with capacitors or really, any SMT passive that has end-covering terminals.
Putting them in parallel though does have the added benefit of lower current through each. I wouldn’t design around that though and just make use of the benefit.
Actually it’d be easier to stack them on-end rather than on top of one another. i.e. place them on their sides.
That’s how i’ve been doing it. Also makes it possible to read the values of each resistor. Sorry for reporting your comment, the buttons were stacked on top of each other (what a silly thing to happen while talking about stacking resistors…)
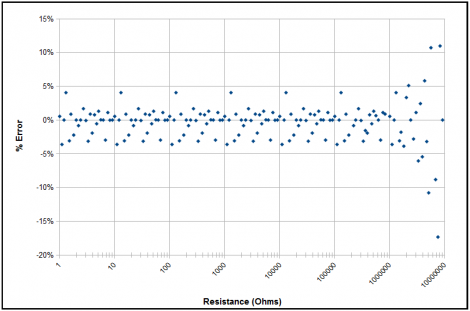
interesting how the graph looks kind of like a double helix
Yup I buy ALL OF THEM. a $40.00 kit will give you more resistors than you will ever need, and restocking costs me about $7.25 a year at a 100 a time for the same value. (buy in bulk and save!)
Ok, 2 questions:
Where are these $40 SMD resistor kits?
Are there capacitor kits?
Bonus challenge:
What’s the best way to organize all these strips of tape!?
Have a look on eBay, you can get resistor and capacitor kits for a lot less than that.
Binders with strips are what I have found most practical, and you can get them from 1206 to 0201 for resistors, and quite a few different packages for capacitors.
What do I win?
https://www.adafruit.com/products/442
https://www.adafruit.com/products/441
these should answer all 3 of your questions.
Digikey. Search for “smt resistor kit” — price varies with size of part, number of parts and packaging. PHL2-KIT-ND, for example, is 1100 0402 resistors for $37.
As far as organizing: I have one of those cabinets with small plastic trays in it. I group 3-4 values in each, cutting the tape to a reasonable width so they sit flat in the drawer. If you want to be more organized than that, you can get binders with plastic inserts (for film negatives?) or just tape the strips together at one end and label the bundle with the resistance value.
@fred
Fancy-pantsy! You win my gratitude! :)
I like these kits:
http://www.sureelectronics.net/goods.php?id=159
The flip top lid boxes are very convenient. I absolutely hate peeling back tape to get to components, you always drop at least one of the bastards.
@sneakypoo
Those look very nice! Also, the price is very good. However, they’re all 0805! Something to think about. Luckily, if you’re careful, you can use 0805’s on 0603 pads provided there’s enough room around it.
Heh, I just bought and USED up about $300 worth of resistors, all 0603s
Damn, Mike, that is a pile of resistors. What did you build?
I have the adafruit resistor books and love them, though they need to hurry up and sell empty pages to add to them.
Some years back I wrote a JavaScript Tool that runs in a browser (works at least with firefox) that can calculate networks of up to three e6 resistors to fit any given resistor value:
http://svn.clifford.at/tools/trunk/electrotools/rcalc.html
Aren’t the values in a resistor series already at the optimum values for producing new resistor values? That is the whole point of using preferred numbers. I say buy a resistor kit and lots of extra 1k, 10k, 100k, and common LED resistor values and be done with it.
no, the resistor values are such that each value is 1.2 times bigger than the last
The E12 series is
1, 1.2, 1.5, 1.8, 2.2, 2.7, 3.3, 3.9, 4.7, 5.6, 6.8, and 8,2 then all those values in multiples of ten.
of course you can make an 11 ohm resistor by getting a 10 ohm, and using a 1 ohm resistor in series, or you could use either a 10 ohm, or a 12 ohm resistor as a best match.
The series is not designed for easy adding (though has that benefit), it’s designed that you can use standardised component values that are never more 10% away from the intended/designed values.
jethomson, thanks for posting that link to “preferred numbers”. I’ve never heard of that before, and it answers my long standing question regarding the popularity of resistor values like 47k opposed to 50k.
Possibly Stupid Question Alert
Wouldn’t the “path of least resistance” defeat stacked resistors? Why would the current go through all of them instead of just the one with the lowest value?
When you think of it that way, it doesn’t make sense, does it?
It may help to think of it using the common water and pipes analogy. Assume that voltage is water pressure. A pipe is wire. Think of a resistor as a constricted pipe. It restricts the flow of water such that the pressure difference on either side of the constriction changes relative to the flow. If there’s no current the voltage is the same, if there’s lots of current then the difference is large. (just like ohms law) Now, let’s add pipes in parallel. When we add more pipes in parallel isn’t not so much a “path of least resistance” as it is a sharing or the current carrying capacity, if that makes sense.
I hope I haven’t offended any hard-nose EEs out there, that’s just the way I think of it.
The path through the higher resistance is still a complete circuit. More current will flow through the path of least resistance, but current will still flow through the higher resistance.
For example, the headlights on a car will have less resistance than the dome light (and therefore draw more current), but the dome light will still work even if the headlights are on.
Electricity doesn’t flow through the easiest path, it flows through *all* paths. Of course more of it flows through the easy paths than the hard ones.