The idea of using nanobots to treat diseases has been around for years, though it has yet to be realized in any significant manner. Inspired by Purcell’s Scallop theorem, scientists from the Max Planck Institute for Intelligent Systems have created their own version . They designed a “micro-scallop” that could propel itself through non-Newtonian fluids, which is what most biological fluids happen to be.
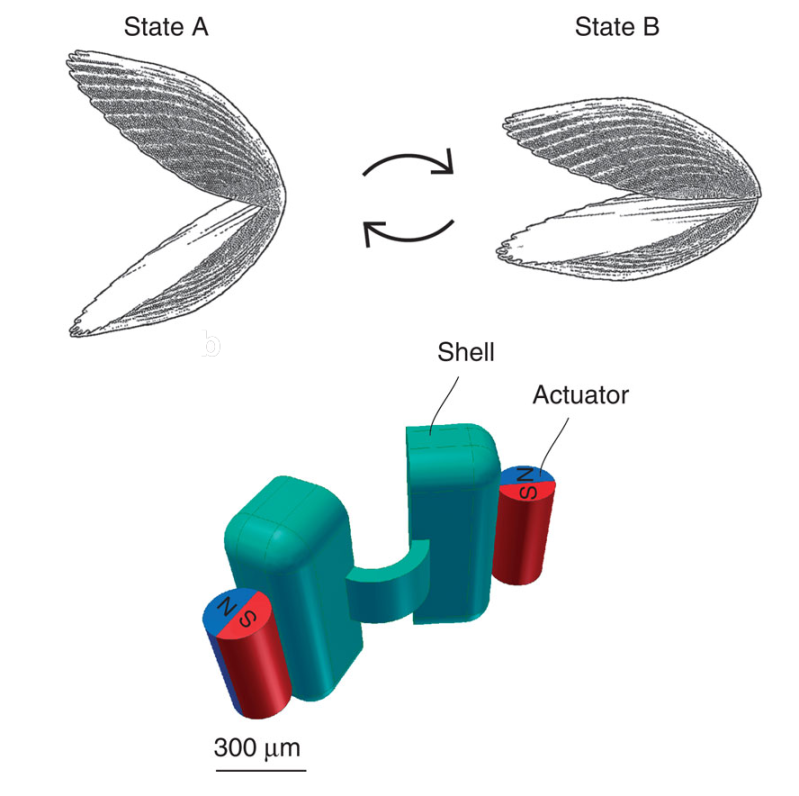
The scientists decided on constructing a relatively simple robot, one with two rigid “shells” and a flexible connecting hinge. They 3D-printed a negative mold of the structure and filled it with a polydimethylsiloxane (PDMS) solution mixed with fluorescent powder to enable detection. Once cured, the nanobot measured 800 microns wide by 300 microns thick. It’s worth noting that it did not have a motor. Once the mold was complete, two neodymium magnets were glued onto the outside of each shell. When a gradient-free external magnetic field was applied, the magnets make the nanobot’s shells open and close. These reciprocal movements resulted in its net propulsion through non-Newtonian media. The scientists also tested it in glycerol, an example of a Newtonian fluid. Confirming Purcell’s Scallop theorem, the nanobot did not move through the glycerol. They took videos of the nanobot in motion using a stereoscope, a digital camera with a colored-glass filter, and an ultraviolet LED to make the fluorescent nanobot detectable.
The scientists did not indicate any further studies regarding this design. Instead, they hope it will aid future researchers in designing nanobots that can swim through blood vessels and body fluids. We don’t know how many years it will be before this becomes mainstream medical science, but we know this much: we will never look at scallops the same way again!
The video below shows an example of the nanobot with asymmetric, symmetric, and no actuation. It is one of many AVI files linked in the paper, so you may need to paste the link in your address bar to open it:
http://www.nature.com/ncomms/2014/141104/ncomms6119/extref/ncomms6119-s10.avi
For something a bit more basic, here is another video explaining the experiment and non-Newtonian fluids:
[via Engadget]















Well, wow. We really need to switch from microbots to nanobots though. STL printers anyone?
That’s kindof how actual scallops work, and I’m pretty sure sea water is Newtonian. The difference from reading the link seems to be the scallop opening slowly, and snapping shut.
I’ve sometimes thought about doing that in space. Floating free in empty space, would bringing your legs up to your chest slowly, then springing them back, like swimming, propel you forwards? In that case it’d work with no medium to splash about. Is it something to do with the momentum (correct word?) of an object being mass x (velocity squared)?
Something like how it’s possible to propel a playground swing just by kicking into space. Or similar with an office chair. I wonder if that’d work as a reactionless drive for submarines?
“Floating free in empty space, would bringing your legs up to your chest slowly, then springing them back, like swimming, propel you forwards?”
I think you will most likely just wobble on the same spot.
Yes, your center of mass will stay in the same place the whole time just like with rockets in space.
Let’s not get into Dean drives and other inertial drive pseudoscience here.
Movement within one inertial frame can sometimes appear to be reaction-less. But movement without reaction on a large scale would defy Newtonian laws of motion.
I think kicking a swing works because you change your center of gravity (which means you need a significant gravity gradient for it to work; hence: not in free-fall/micro-gravity).
You might be right about the office chair thing, but wouldn’t that only allow you to spin in place? We need some ISS orbitnauts to weigh in here, I guess ;)
For submarines, I assume the highest efficiency will always be had with some form of swimming (i.e. pushing and pulling on the water itself).
That action works while swimming because you have water to push against. As you move you create areas of lower density and higher density around you. When you flail on a playground swing or a wheeled chair, you are putting your energy into the system but also changing the center of mass of the system such that instead putting that energy into slowing down or letting it decrease as sound or heat or chaotic movement, you are helping the system move in a certain way.
Actually, the key reason why scallops can swim in a Newtonian fluid is that they are much larger – this means that their Reynolds number is larger than for objects at the scale of this microbot. The scallop theorem only holds at low Reynolds numbers (i.e. non-turbulent flows).
Intuitively, if you have no turbulence, then forward and backward motion cancel each other out in a Newtonian fluid. If you have turbulence, you can “ride” an eddy and get a net motion in one direction. At smaller scales, it is much harder to create turbulence than at larger scales in the same medium (the Reynolds number is essentially a measure of how easy it is to create turbulences in a specific medium at a specific scale).
A basic principle of physics is that total momentum is conserved. In space, assuming there is nothing that you can pass momentum to or that can pass momentum onto you (i.e. not even to a viscous surrounding atomic/molecular medium), your total momentum, which is equivalent to the momentum acting on your center of mass, couldn’t change appreciably (I think that the density in outer space is of a few atoms per cubic meter). Thus, in space no matter how you move your limbs or rotate your body, it would be quite correct to say that you would not be capable of translational movement relative to other bodies, unless by gravitational effects caused by nearby bodies. Your only chance would be throwing whatever you have with you and can dispense with towards the direction opposite of your travel destination.
66
When a gradient-free external magnetic field was applied, the magnets make the nanobot’s shells open and close. These reciprocal movements resulted in its net propulsion through non-Newtonian media.
99
So where does the energy come from? This statement seems to suggest free energy. A static magnetic field can’t cause reciprocating motion.
Here is an excerpt from the paper that explains the gradient-free magnetic field in more detail:
“…asymmetric actuation of the two shells is achieved by applying a periodic exponentially decaying current to generate the magnetic field. Typically, a 0.5-Hz waveform was used with a slow ~1.9 s exponential decay, followed by a rapid 0.1 s ramp. Since a gradient-free field is used, the micromagnets do not experience any pulling force, which ensures the net displacement of the microswimmer is because of the propulsion caused by its own shape-changing swimming motions.”
anyone can tell me how to compute drag force in non-Newtonian fluid.