It’s not surprising that Analog to Digital Converters (ADC’s) now employ several techniques to accomplish higher speeds and resolutions than their simpler counterparts. Enter the Delta-Sigma (Δ∑) ADC which combines a couple of techniques including oversampling, noise shaping and digital filtering. That’s not to say that you need several chips to accomplish this, these days single chip Delta-Sigma ADCs and very small and available for a few dollars. Sometimes they are called Sigma-Delta (∑Δ) just to confuse things, a measure I applaud as there aren’t enough sources of confusion in the engineering world already.
I’m making this a two-parter. I will be talking about some theory and show the builds that demonstrate Delta-Sigma properties and when you might want to use them.
ADC Architecture
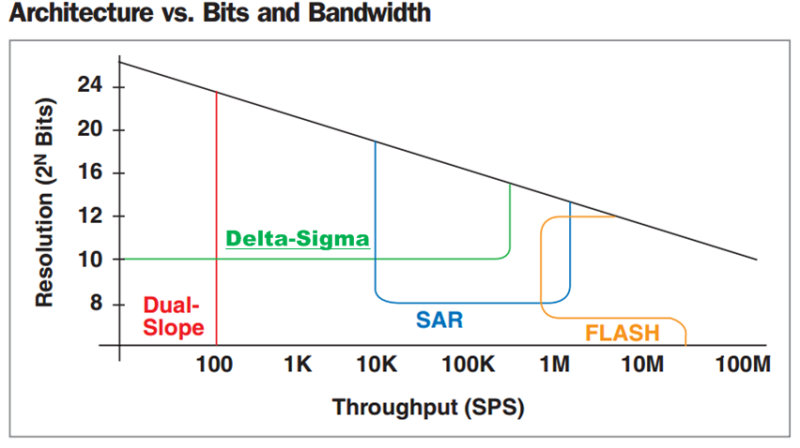
Looking at the diagram below we see four of the most prevalent ADC technologies to include Delta-Sigma . We covered SAR, Flash and Dual-Slope in the last post and each had their particular area where they did well. Sigma-Delta offers a combination of high resolution and moderate throughput.
Delta-Sigma Block Diagram
A block diagram of the Delta-Sigma converter shows three main sections: The Delta-Sigma Modulator, and the two part digital filter that combines an Integrator and a Decimator.
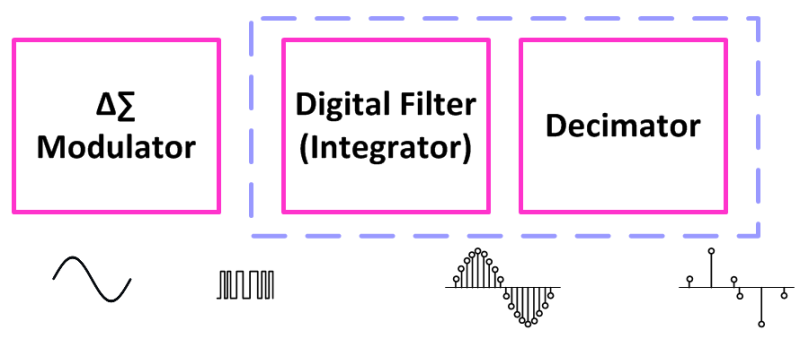
The job of the Modulator is to convert the analog input into a single bit modulated digital stream. The Integrator accumulates this single bit stream into a multi-bit value representing an average of the signal but with lots of extra information. Finally the Decimator removes the extra unneeded information resulting in an output that is accurate but adheres to the correct minimal size.
Delta-Sigma Modulator
The Delta-Sigma Modulator is the core of the ADC and is responsible for digitizing the input analog signal while reducing noise through a couple of techniques, namely oversampling and noise shaping.
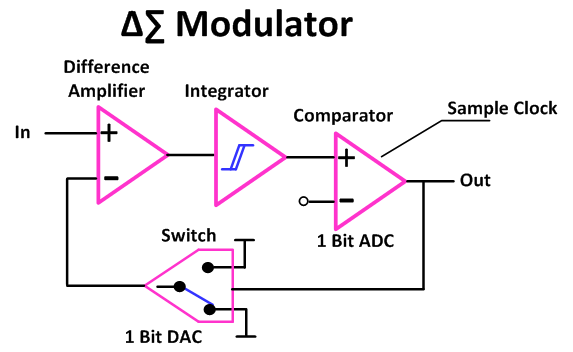
As seen in the block diagram here, the Delta-Sigma Modulator consists of a difference amplifier that sums in the feedback of the output, an integrator which acts as noise shaping in that it removes noise in the lower frequencies, a 1 bit comparator, and a switch which effectively feeds back an inverted form of the results of the last sample. Due to the feedback path the digital output represents the difference in signal from sample to sample.
To demonstrate that there really is a sine wave hidden in the digital hash I set the oscilloscope to average the input over several samples.
Quantization Noise
In any ADC there is a noise or error term due to the inaccuracies of the quantization process, which is called… wait for it… quantization noise. This is essentially the difference between the real value and the perceived value as sampled by the ADC.

The higher the resolution of the ADC the less noise there will be as a result. This is true to the point where we can state mathematically that the Effective Number of Bits (ENOB) of the ADC can be determined by the ratio of the signal amplitude to the quantization noise amplitude known as the Signal to Noise Ratio (SNR). Note that I am ignoring all of the other sources of noise and non-linearity for the purposes of this discussion.
ENOB = (SNR-1.76)/6.02db
Likewise we can predict the SNR due to quantization noise based on the resolution of the ADC (N)
SNR = (6.02 x N) + 1.76db
The Frequency Domain
In order to display the amplitude of a signal compared to the noise we can view everything in the Frequency domain such as the output of a spectrum analyzer. When viewed in the frequency domain the left side of the display typically represents the lowest frequencies with high frequencies on the right. The amplitude of signal is represented by the height with greater amplitude at the top. This is not to be confused with the time domain which is what we typically see on an oscilloscope.
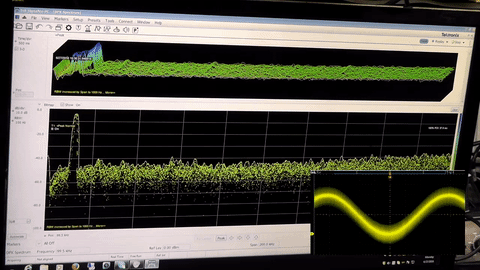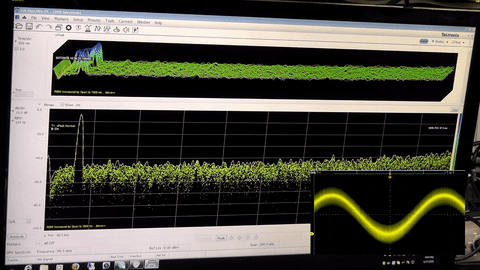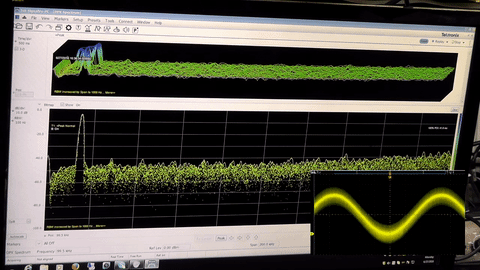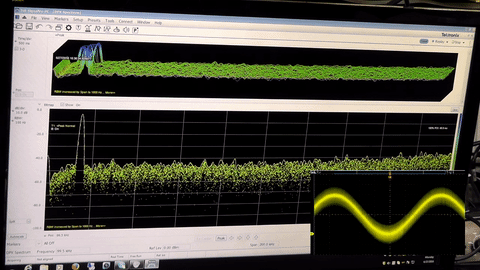
Insert: Time Domain
Here the frequency domain is the large display and the time domain is in the inset on the bottom right. Changing the frequency causes the “hump” to move left to right on the main display while the effect can be seen in the time domain as a change in cycle time.
Oversampling
A very effective noise reduction technique is to increase the sample frequency, a technique known as oversampling. This has the effect of taking the quantization noise and spreading it out over a larger part of the spectrum. In a following step a filter is applied to remove the noise in the portion of the spectrum that is only inhabited by the noise we induced. So while it’s not really removing the noise outright, it is reducing the noise in amplitude in the area of interest near our signal. A basic rule of thumb is that for every 4x increase in sampling frequency the effective number of bits (ENOB) will increase by one.
Here we can see oversampling in action: Note the change in noise level when changing the sampling clock from 5Mhz to 20 Mhz.
Noise Shaping
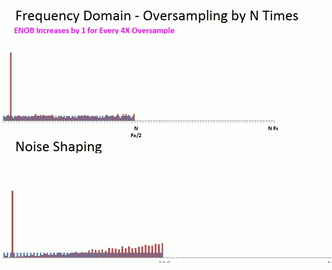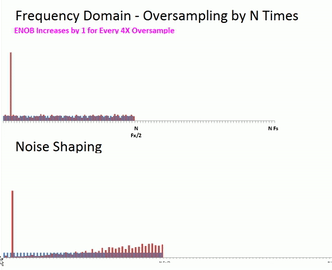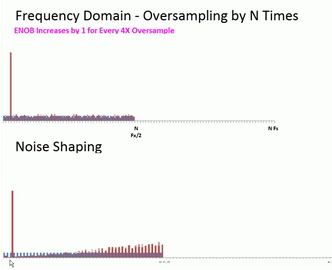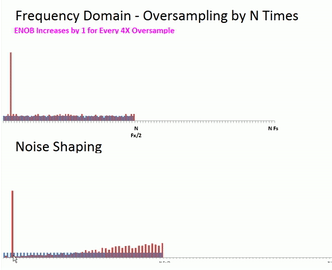 The Delta-Sigma ADC utilizes this noise reduction technique but then goes one step further utilizing a technique known as noise shaping. As the Delta-Sigma modulator uses an integration stage or two, it has a natural traffic shaping effect where the noise at the low end is reduced at the expense of the upper end of the spectrum. Once again we aren’t really removing the noise outright, but it is reducing the noise in amplitude in the area of interest near our signal.
The Delta-Sigma ADC utilizes this noise reduction technique but then goes one step further utilizing a technique known as noise shaping. As the Delta-Sigma modulator uses an integration stage or two, it has a natural traffic shaping effect where the noise at the low end is reduced at the expense of the upper end of the spectrum. Once again we aren’t really removing the noise outright, but it is reducing the noise in amplitude in the area of interest near our signal.
Using the ADC Evaluation Software to display the noise shaping.
The combination of these technique is the basis for the high resolution of the Delta-Sigma ADC (remember low noise allows high resolution).
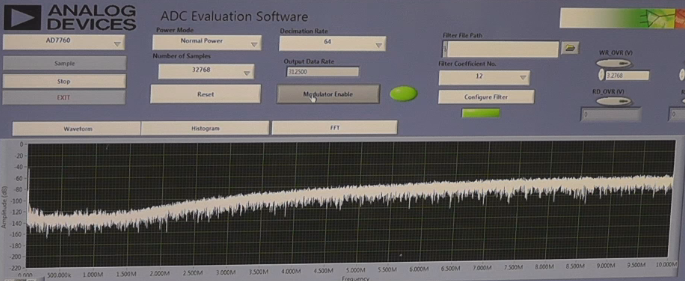
These are the basic concepts behind how Delta-Sigma ADC’s work. In the next part of this series I will demonstrate how to create a digital filter and show some live results on the bench. Here’s a shot of that hardware to whet your appetite. Subscribe to our YouTube channel and keep an eye on the front page for that next installment. You can also check out the Bil Herd Originals video playlist to hold you over until the next one is ready.
Let me know any questions you have in the comments below and I’ll try to work the answers into the next article.






















I’m so glad Hacakday is covering this little bit of engineering ingenuity. I love sigma-delta ADCs, and sigma-delta modulation in general. You can buy ICs that modulate for you and provide a bitstream, but the core concept can be used in far more places.
Want a fast DAC, but only have digital pins? Sigma-delta modulate! Want an ADC, but stuck with digital pins again? Sigma-delta modulate (with the aid of an op-amp)! Need to compress a wide digital word while minimizing rounding error? Yep, sigma-delta again! You can even generate useful RF signals with it!
So what I’m saying is, if you like hacking with FPGAs, pay attention to this, because it can be a quick way to handle analog signals without needing dedicated external ICs.
I show a little bit of FPGA with a Cyclone IV in part 2.
If you have a way to demonstrate SD ADC with a couple digital pins I would love to see a description! I have a big fat book on Oversampling Delta-Sigma Converters (they do delta first after all – with Sigma-Delta for DAC) I got it with the intention of doing a discrete built converter as a lab exercise. I never got around to it and the book was ALL converters built as IC’s and using all the design tricks available in CMOS.
I show a couple of ways I played with SD in part 2 but ended up with a single chip module the AD7403 for best results demonstrating SNR changing with sample rate, etc. I even made a PCB that showed up too late to be in the video.
Well technically he said he could create a SD *DAC* with a couple digital pins. This is pretty easy to do with some very simple discrete time delta-sigma code. The modulator output can then be passed through a simple RC low-pass filter to generate the analog signal using just a single digital pin. I just threw together a simple C example of this here:
https://gist.github.com/phreaknik/f6b1d2347a84bf032e3c3b3bcf6116b2#file-dt-delta-sigma-modulator-example
As far as creating an SD ADC with digital pins, you would at least need an external comparator (or opamp) and then a DAC output to compare the analog signal to (this could be done using the software SD DAC described above + an RC low pass filter).
Crap, the link didnt post… Here is the link to the SD DAC example code:
gist.github.com/phreaknik/f6b1d2347a84bf032e3c3b3bcf6116b2#file-dt-delta-sigma-modulator-example
Some MCU have internal comparators so a delta-sigma modulator/demodulator could be done using only an MCU and external passive components. A conversation can be sampled at 7Khz so a simple dictation machine could be done with a cheap 8 bits PIC MCU (some have 2 comparators) an some I2C FLASH memory chip to store data.
Yes, which is why you see a PSOC-5 in one shot as you could do the switch and the integrator in theory also.
There are a few ways you can make a SD ADC with digital pins alone. One way is to use an LVDS differential input pair and a single-ended output, like Lattice shows in an App Note (see the end of this post). The LVDS input buffer acts as the comparator, and an RC filter on the feedback from the registered signal acts as your integrator. The clock on which the digital input is registered determines your SD sample rate. The RC filter output goes on the LVDS negative side, and the analog input goes on the LVDS positive side. This works, but it uses more pins than strictly necessary, and a passive, first-order system won’t give you very good results.
To reduce pin count, some FPGAs have internal comparators that compare against a reference voltage. Xilinx makes FPGAs with SSTL3 logic inputs that do this. Go to Xilinx UG381, pages 27 and 37-38 for info on it. The short of it is this: tie the VBIAS pins of one bank of your FPGA to 3.3V/2, and set your analog input pins to be SSTL3_I using this in your UCF file: NET “adcInXXX” IOSTANDARD = SSTL3_I. Then, put a capacitor on the digital input, a resistor between the digital input and analog input, and a resistor between the digital input and the digital output.
You can get fancier with the input logic and use an op-amp based integrator on it (or even a second-order integrator). Unfortunately, all designs I have for those are proprietary. If you can picture an op-amp integrator with differential inputs, you’re on the right track to how to do this.
By the way, I have some related Verilog code stored in my mess of a repository . Look in the sigmaDelta folder for some DAC modules, and I’ve got a sinc-cubed filter under smallFilters/sinc3Filter.v. It’s darn near optimal for Xilinx parts.
Lattice App Note: http://www.latticesemi.com/view_document?document_id=36525
Xilinx SelectIO Information: http://www.xilinx.com/support/documentation/user_guides/ug381.pdf
My Verilog Repository: https://github.com/Cognoscan/BoostDSP/tree/master/verilog/src
Switched capacitors…
One trick I used ages ago (prior to the rise of the WS28xx chips, kind of killed the project at https://github.com/Entropy512/I2C_RGB ) was to use Atmel’s AVR soft-PWM appnote but get more resolution than 8 bits.
The problem is, if you wanted to use Atmel’s appnote and just crank up the bit count, you would absolutely kill performance because 16-bit math is MUCH slower.
So I used a sigma-delta modulator driving the soft-PWM. (Sigma-delta DACs don’t HAVE to be built around a 1-bit DAC, they can take any resolution DAC and trade bandwidth for more resolution). This allowed me to get around 12 bits of resolution for smoother dimming, however at the cost of the effective bandwidth being low enough you could start seeing flicker at extremely low brightness (e.g. when the sigma-delta was modulating the soft-PWM between 1 and 0 brightness) This would keep the 16-bit math running infrequently outside of the timing-critical 8-bit soft-PWM loop.
I “Love” ye Bill! Should had a teacher with your background back in them high-school days. Got a fairly good background then though and appreciate every bit and detail in these posts, keep’em coming!
Now this is cool. Not only some really neat Analog Devices parts, but he’s also using what looks like a Cypress PSOC 5LP development board to drive it all. No Pi, no ‘duino, just real hardware.
Yeah I grabbed the PSOC5 as it had a digital filter in it and the makings of an DS converter (switch, opamp, etc). The digital filter was a FIR instead of a CIC so I concentrated more on FPGA in part 2 but it’s still very cool to have an analog frontend complete with dig filter. Also has its own DS converter which was pretty serviceable.
The problem I had with doing a discrete + software version is that all the monolithic devices do the digital filtering and noise shaping and filtering with clever arrangements of arrays of clocked switches and caps. What might be algorithms in a slow demo are transposed to a hardware domain. All the texts and references I found (and this was over 15 years ago so ?) were for monolithic devices and proposals.
A discrete description with comparators and op-amps + software on an Arduino would be king cool and very handy in education since you can get to all the signals and states. This still itches in the back of my melon.
I show the schematic to a single and second order modulator in Part 2 though it comes with the standard “your mileage may vary” type warning as when I am designing for a video I am doing the minimal amount of work to demonstrate my point.
It’s a [pretty impressive package for $10:
http://www.cypress.com/documentation/development-kitsboards/cy8ckit-059-psoc-5lp-prototyping-kit-onboard-programmer-and
That gets you the built-in SAR and delta-sigma ADCs, plus op amps and a bunch of digital logic to play with.
And if you don’t need the PSoC 5LP, you can get a similar board for the PSoC 4 for only $4!
That W’paedia quantization noise image is simply wrong, though it’s been around forever. You can’t compare a zero-order-hold signal to a continuous time one in a meaningful way.
If you like this kind of thing, check out:
http://www.edn.com/design/systems-design/4421064/Intuitive-sampling-theory–part-1
In the video I mention that there are different ways to model the error/noise and that people won’t necessarily agree. I believe that wikipedia image is close to the Deterministic Sawtooth Waveform Error Model, in the video I mention that some may model it as sine waves, etc. but what I spend some time showing is that the measured value at a point in time that is different from the “real” value, so I do away with a waveform for purposes of discussion.
The main point is that differences in amplitude from the real value contribute to the SNR and that adding bits or oversampling decreases noise.
it is the usual case of “you can’t do that” says the mathematician, “sure, but it’ll do as an approximation” says the engineer and they are both right
I occasionally go off on the fact that hard drives don’t really work based on observing the analog signal, but boy they sure give the appearance of working when you store a file on one. Same with an approximation, I can make something appear to work for all intents and purposes.
I have to mention decimation. I don’t know why – it’s a Sheldon Cooper thing. A word appropriated by news writers/readers because it sounds dramatic. They like to say “the enemy was decimated!” or “the tornado decimated the town”. Then it showed up in DSP work as meaning samples are removed or down sampling.
But as one might gather from the word, it means to kill 1 in 10. It was not a term used for battle, but for punishment by the Romans. A conquered town that shows resistance might have the town’s men “decimated” by counting them off. Julius Caesar in his accounts of the Gaelic Wars has a legion or large group in his forces decimated for showing cowardice. They lined up and counted off and every 10th one stepped forward to be executed. (I think you tell them about the decimation after the lineup.)
So, it came to mean anything that involves removing or losing 1/10. Factors of 10 are not so handy in binary. We should really have octimated and heximated, etc. Nibblemated? Hmmm.
Aside from nit picking, it would be nice to have precise terminology for this kind of thing. Any suggestions?
In Part 2 I talk about the CIC filter a bit more and show different decimation rates, etc. I also pointedly avoid defining the origin of the term and just refer the gentle viewers to look it up for themselves.
Insteresting historical note about the origin of “decimation” but words often loose their true meaning in vernacular usage so you have a lot of nit picking to do.
Ya, thats why I sidesteped the issue in the video and tell people to look it up if interested. I did actually make a joke that it was where Roman soldiers would pick on each other’s cooking or some such thing but I decided to cut that bit out.
Is it just me, or is there something a little bit weird about bringing a signal in on a bit of decent coax, into an SMA connector, into a SMA end-launch connector on a PCB… which is then plugged straight into a dirty old breadboard?
Seems like a waste of money. Simply using a bit of coax with the centre conductor stripped, tinned and jammed into the breadboard would probably give you exactly the same performance.
Yeah, not going to cut the ends off my SMA/BNC cables so I can jam it in a bread board. Once the SMA boards were made I can just lift them out and plug into the next board for the next shoot. One thing I detest more than solderless breadboards is an intermittent connection, especially in the middle of trying to narrate.
Thanks Bill, looking forward to the next video.
I may be wrong but doesn’t oversampling only work when the noise source is truly random?
Isn’t that why when making an ADC over sampler one can also inject a known random noise source?
I liked the write up, good work.
It works on the random noise that is due to quantization error. One way to make noise more random in the instance where the noise is correlated (I.E. there is some kind of non-random relation) is to inject random noise, a process known as dithering. Seems counterintuitive to add noise to reduce noise but it works.
I really like the ressources TI has put together on the complete analog-digital signal chain.
Go have a look at http://www.ti.com/lsds/ti/analog/dataconverters/learning_center.page
Lots of information and most of it was really helpful to me.
Cool link. I also have a list of links but it became so wide of topic and long that it was too unwieldy to post.
Excellent work Bil – all the examples bring the concepts to life. I’m curious about what oversampling does to the performance of an ADC. Also can you describe the set-up you’re using to look at the frequency domain?