Just how much metaphorical juice is in a coin cell battery? It turns out that this seemingly simple question is impossible to answer — at least without a lot of additional information. The problem is that the total usable energy in a battery depends on how you try to get that energy out, and that is especially true of coin cells.
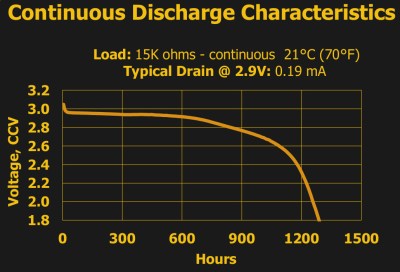
For instance, ask any manufacturer of the common 3 V lithium 2032 batteries, and they’ll tell you that it’s got 230 mAh. That figure is essentially constant across brands and across individual cells, and if you pull a constant 0.2 mA from the battery, at room temperature and pressure, you’ll get a bit more than the expected 1,150 hours before it dips below the arbitrary voltage threshold of 2.0 V. Just as it says on the tin.
What if you want to do anything else with a coin cell? Run an LED for a decade? Pull all the energy out right now and attempt to start a car? We had these sorts of extreme antics in mind when we created the Coin Cell Challenge, but even if you just want to do something mundane like run a low-power radio sensor node for more than a day, you’re going to need to learn something about the way coin cells behave in the real world. And to do that, you’re going to need to get beyond the milliamp hour rating. Let’s see how deep this rabbit hole goes.
Energy and Internal Resistance
A coin cell battery is essentially a metal jar of chemistry constructed so that one side wants to give up electrons and the other side wants to take them in. You could imagine measuring the capacity by counting up the number of electrons that want to trade places before their willingness to move, measured in volts, drops below a certain threshold. It’ll be a big number, but that’s why we have the coulomb, a unit of charge equivalent to roughly 6.24 x 1018 electrons’ worth. Or you could use the ampere, a measure of flow of charge equal to one coulomb per second, and multiply by time to get back to a total charge. One amp-hour is exactly 3,600 coulombs.
And no matter which definition physicists decide is primary, a milliamp hour isn’t a bad way to think of the amount of charge in a coin cell. For a 230 mAh cell, you’re probably going to get 460 hours at half a milliamp of draw, and you are also likely to get something near 230 hours at 1 mA. But will you get ten hours at 23 mA? 0.23 hours at 1 A? The answer is “no”. Pretty soon, the milliamp hour rating gets stretched to breaking, and the reason is internal resistance.
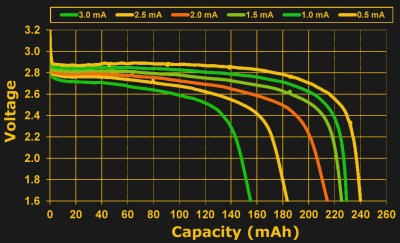
Batteries have a reluctance to trade too many electrons too fast, reflected as a resistance. Try to pull too much current from a battery, and it obeys Ohm’s Law: 
So you’ll be able to draw more total energy from a battery if you pull it out slowly, breaking the simple multiplicative milliamp-hours relationship. Not coincidentally, manufacturers tend to rate the batteries at fairly low average currents: from a fifth to a half of a milliamp.
But there are two more wrinkles in the internal resistance story before we’re through. Batteries can support short bursts of current output before the internal resistance rises. Equivalently, they can supply short bursts of current before the voltage drops to its steady state value. That means that you’ll get more total energy out of a battery if you give it some time to recoup between high current pulses. This excellent white paper (PDF), written by folks at Nordic Semiconductor and Energizer, has some great experimental data. The takeaway is to let your batteries rest for 25 ms or more between pulses if you can help it.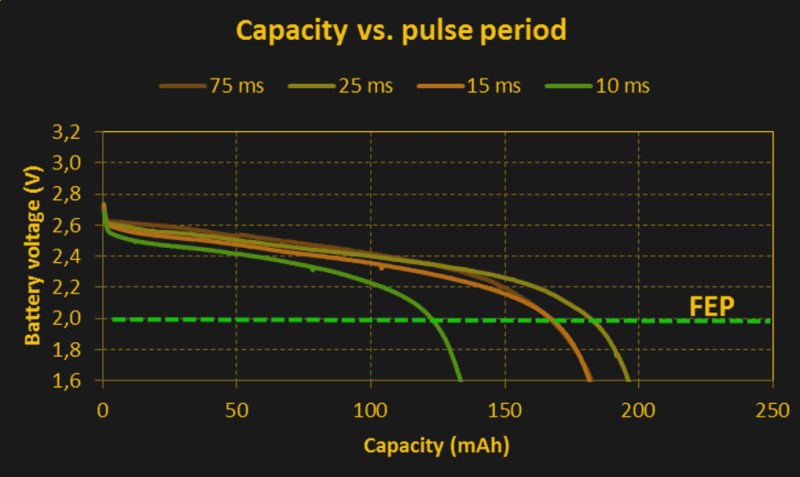
Finally, internal resistance is also a function of charge state, being lower in the beginning and increasing as the battery’s supply of mobile electrons is depleted. Toward the end of the battery’s maximum rated capacity, as this internal resistance increases, you simply might not be able to pull out the multi-milliamp peak currents that were previously feasible without the voltage sagging and potentially browning out your device. This further shortens the useable life for higher currents.
That wraps up the physics-slash-chemistry lesson. As you can see, there’s a lot involved in getting the maximum bounce per ounce out of a coin cell; the milliamp hour rating comes from one simple usage pattern that might not have anything at all to do with your application, and there are design tradeoffs aplenty. We’d bet that there are even more odd behaviors lurking around some dark corners.
The Long Run or Burning Bright
If you want to get the most out of a coin cell, you’ll go low and slow. And if that’s not a possibility, peaky current patterns with longer pauses between peaks is almost as good, but you should think about brownouts near the end of the battery’s life. Either way, it absolutely pays to treat the rated capacity as a maximum that’s only specified at the rated current. And if you’re designing for reliability, you’ll still want to do some worst-case analysis and testing, and note that different manufacturers specify different rated currents — be sure to check the data sheet. Of course, what’s best for battery capacity may not be best for your project, and there’s something to be said for just making it work at all, efficiency be damned.
But that’s what we think is fun about working with coin cells. They provide very limited resources, so that every choice matters. Using coin cells forces you to focus on your power budget in a way that tossing a rechargeable lithium-ion battery pack into a box doesn’t. We hope that the lessons learned in the coin-cell playground will be more broadly applicable, and that you’ll all share what you find. If you find anything fun, enter it in the challenge or just let us know.
“Equivalently, they can supply short bursts of current before the voltage drops to its steady state value. That means that you’ll get more total energy out of a battery if you give it some time to recoup between high current pulses.”
I read the linked PDF, and I did not see this. In every test case, the pulsed current tests performed worse than the equivalent constant current. In fact, the oddest result was current bursts at a 25ms period performed better than the tests at a 75ms period, which is kind of counter to what this quote says.
…which makes you wonder why the whitepaper authors didn’t just drop a big capacitor across the cell to average out the current pulses. I’m guess space and cost are the answer, but you could certainly do it.
A capacitor wouldn’t change anything as the cell will have to recharge the capacitor after the pulse. It would only create a lag in the cell current draw. What that count is the total energy spent and a capacitor don’t change that accept for adding the capacitor leakage current to spent energy.
correction:
…except for adding the capacitor leakage current to spent energy.
The old zinc carbon alkaline cells had a property of high internal resistance, but at the same time they had an electrolytic capacitor effect where the battery could be pulsed at high currents for a few seconds and then left to rest.
Hence the name “flashlight” – you would literally flash the light as it woud not stay on.
Have a look at this paper from Texas Instruments. It shows how capacitors can increase the life of a cell battery. http://www.ti.com/lit/wp/swra349/swra349.pdf
The important factor is mitigating the burst load on the battery and therefore increasing its lifespan even with losses due to capacitor leakage.
For a given average draw, I^2R losses always favor the steady current, for sure. (The average value is the minimizer of the sum of squares.)
If you’re pulsing, like making infrequent transmissions from a radio, the fact that internal resistance increases over a 10-100 ms timescale favors shorter pulses. My layman’s read of the chemistry is that there’s some free-er electrons just kicking around, but once they’re exhausted, some slower chemical reactions need to occur to replenish them.
Longer recoup times (holding pulse current constant) also seem to help efficiency, with the weird glitch that you (and the authors) note between 25 and 75 ms. I don’t hold that for significant, because we don’t really know how many times they repeated each setup. (Looks like just a handful.) But the trend is there in their data, right?
In recoup-time tests, the long-run average current is varying, so they’ll have different wall-clock lifespans as well. But multiplying the average current by that lifespan gives the total capacity, which is what they’re actually comparing.
Does that fit your read of the paper?
In some (most?) battery types, the side reactions happening at the electrodes cause a quick increase in R in prolonged discharge, so while the I^2 portion will favor steady current draw, the effect is offset by having low R at the beginning of the discharge.
With a 75ms rest, to maintain the same overall draw, more must be drawn during the non-rest portion of the cycle… and they bump up against more internal resistance.
They’re not trying to hold the average draw constant, though. (Peakier is worse than flatter if you’re holding average current constant across setups, as you note.)
The batteries with 25 ms rest expire (a bit more than) 3x faster than those with 75 ms rest. Once you multiply the wall-time by the average current, though, you get the total power extracted, and that’s higher for the batteries with longer resting periods.
Maybe longer total time makes self-discharge more significant in overall sum of losses?
Entirely unrelated to the article, I have to say I’m actually really amused/pleased by the amber-on-dark-grey graphs.
The colors have the less hideous default CGA palette look. Perhaps the next article with graphs will be done in shades of cyan and magenta, with white? :)
Not entirely off-topic: my background screen is #1A1A1A and the highlight color for an active window is #F3BF10. I actually live in a Hackaday-color-scheme window manager.
Attempts to get my blood colored #F3BF10 have so far failed, but I’m not giving up just yet.
I really like it the combo of the HaD colors with white accents. I should work on those more.
Sometimes the, old, water analogy is still handy for a teaching aid.
Think of the cell as being similar to a damp sponge and how the moisture poured on one side, wicks/flows through it.
Perhaps a simple visualization aid for the mind, if nothing else.