Specialized tools that focus on one particular job tend to get distilled right down to their essentials and turned in an economical consumer product. One example of this is radius (or fillet) gauges: a set of curves in different sizes that one uses to measure the radius of a curved surface by trial and error. To some, such products represent solved problems. Others see opportunities for a fresh perspective, like this caliper-enabled 3D printed radius gauge by [Arne Bergkvist].
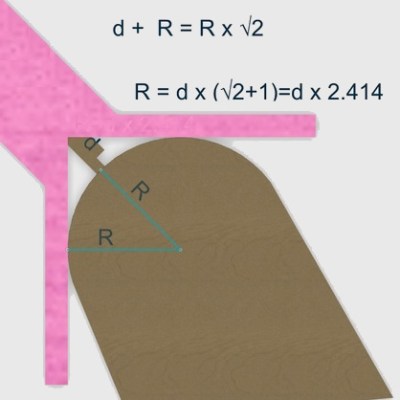
[Arne]’s 3D printed radius gauge is a simple object; a rigid attachment for a nearly ubiquitous model of digital caliper. By placing the curve to be measured between the two arms of the device and using the depth measurement of the caliper to measure distance to the curve’s surface, a simple calculation (helpfully printed on the unit itself) of radius = distance * 2.414 reveals the radius of the curve. However, this shortened calculation makes a number of assumptions and only works for [Arne]’s specific design.
Another version by [Fredrik Welander] represents a more flexible take on the same concept. His RadGauge design (pictured up top) has a few different sizes to accommodate a variety of objects, and his Git repository provides a calculator tool as well as some tips on fine tuning to allow for variations in the dimensions of the printed attachment.
3D printing has opened a lot of doors, and items like this show that the plastic doodads created aren’t always the end result in and of themselves; sometimes they are the glue that enables a tool or part to work in a different way. To help get the most out of 3D printing, check out the in-depth coverage of how to best tap 3D printed parts for fasteners, and [Roger Cheng]’s guide to using 3D printed brackets and aluminum extrusion to make just about anything.

















If the angle between the sides wasn’t 90 degrees, but 60 degrees, the distance would be directly the radius of curvature. At least if my quick check with solvespace is correct..
You’re right. However that wouldn’t be able to measure the radius of rounded corners where the corner is anything more than 60 degrees, which would be a bit limiting if that application is desired.
True, aiming for something like 1:2 ratio might make the angle more practical.
And if you use 91.7 degrees the factor is 2.54 (measure d in cm, get radius in inches) or 105.77 degrees for a factor of 1/0.254 (measure d in inches, get radius in dm).
Of cause the larger angle (and factor) makes the error larger.
Remember that more and more people round their corners with something else than a circle.
But in those cases, radius would be undefined.
For larger diameters you can always make your own piTape as explained in this (https://www.youtube.com/watch?v=5hQ1muZG62o) video
Anybody else here bothered by the fact that the measurement demonstrated in the title image is clearly wrong, as the 3D-printed mechanism is far too small for the object being measured?
No, because that’s a different design that’s not intended to have a constant ratio; it is supposed to make contact at the points, and has an app to handle the resulting trigonometry.
Yes, having the two not-entirely-related-but-not-unrelated images so close with no explanation in the caption is confusing. It isn’t clear that the opening paragraph is about the image to the right and not the image above, until the second paragraph, which is about the image above.
If you notice, the one in the picture is measuring a huge candle base.
Make that a filament spool. #GlassesOn
Clever idea. Nice to be able to extend the use of an inexpensive caliper.
FWIW I remixed it here: https://www.thingiverse.com/thing:2811444/remixes which served my purpose, but still needs some updates.
If you want the same tool for sphere, I make it few years ago: https://www.thingiverse.com/thing:270455
Measure with a caliper, mark with a chalk and cut with an axe.