Everyone learns (and some readers maybe still remember) the quadratic formula. It’s a pillar of algebra and allows you to solve equations like Ax2+Bx+C=0. But just because you’ve used it doesn’t mean you know how to come up with the formula itself. It’s a bear to derive so the vast majority of us simply memorize the formula. A Carnegie Mellon mathematician named Po-Shen Loh didn’t expect to find a new way to derive the solution when he was reviewing math materials for middle school use to make them easier to understand. After all, people have been solving that equation for about 4,000 years. But that’s exactly what he did.
Before we look at the new solution, let’s talk about why you want to solve quadratic equations. They are used in many contexts. In ancient times you might use them to determine how much more crop to grow to cover pay tax payments without eating in to the crop you needed to subsist. In physics, it can describe motion. There’s seemingly no end to how many things you can describe with a quadratic equation.
Babylonians, in particular, would solve simultaneous equations to find the roots of a quadratic. Egyptians, Grecians, Indians, and Chinese peoples used graphical methods to solve the equations. The entire history is a bit much to get into, but still a great read. For this article, let’s dig into how the new derivation was discovered.
Setting Up the Equation
So what’s the method? You watch Loh explain it himself in the video, below. Suppose you have a standard quadratic equation for whatever reason that looks like this:
x2-6x+3=0
In this case, A=1, B=-6, and C=3. Note that for Loh’s method to work, A should equal 1, but if it doesn’t you can always divide both sides by A to make that true. For example, consider this equation:
3x2-18x+9=0
It will have the same roots as the first one because if you divide both sides by 3, you get the first equation.
The Polynomial Factor
To factor a polynomial into two binomials we can use FOIL (First/Outer/Inner/Last). So we know that:
x2-6x+3=(x-S)(x-R)
Where we just made up S and R. They exist, but we don’t know what they are yet. However, for the answer to be zero, you can see that the equation will be zero when x=S or X=R so that means S and R are the roots of the equation.
So What’s S and R?
It sounds silly, but let’s multiply out the binomials into another polynomial. Remember FOIL:
x2-6x+3=x2-(S+R)x+SR
If you look at that for a second, you will probably realize that S times R must be 3. We also know they add up to 6. At this point, you can probably just guess the roots, but let’s make it formal.
The roots of a polynomial like this will be in the form of U±z. So if S=U+z and R=U-z, the only way to make (U+z)+(U-z) equal to 6 is if U is 6/2. Since B is -6 in this example, we can intuit that U must be -B/2 in the general case.
Home Stretch
So we now know the roots are -B/2+z and -B/2-z. We know that B is -6. We also know the answer is when we multiply those roots together must be C (3, for our example). So we can write:
(-(-6)/2+z)(-(-6)/2-z)=3
Or:
(3+z)(3-z)=3
Do the FOIL method again and get:
9+3z-3z-z2=3
The middle terms will always cancel out so you get:
9-z2=3
Subtract 3 from both sides and add z squared to both sides:
6=z2
Since the root must be -B/2±z we know that our two roots are 3+√6 and 3-√6.
The Key and the Catch
The point is, none of this was hard to remember or work out. Just remember that you rewrite the zero as (x-S)(x-R) and the rest follows very logically.
The only real problem is not many quadratic equations have A=1. For example, suppose you throw a ball straight up from 5 meters above the ground with a velocity of 15 m/s. We want to know when the ball will hit the ground.
Gravity is going to pull down on the ball at about 4.9 meters per second squared (assuming gravity accelerates at -9.8 m/s2). The physics formula is (at2)/2 so we get our first term of -4.8t2. The second term will represent the speed of the ball which is simply 15t. We also started 5 meters above the ground, so we will add 5 and wind up with:
-4.8t2+15t+5
This formula will tell you where the ball is assuming you throw at t=0. We want to know when it hits the ground so that will be one of the roots:
-4.8t2+15t+5=0
To use the new method, just divide it all through by -4.8 to get:
t2-3.125t-1.04=0
So now B=-3.125 and C=-1.04. We know the root will be -B/2±z or 1.5625 and that z2 will equal (1.5625)2+1.04.
 That’s 3.48 (about) and the square root is about 1.866. The roots, then, are 1.5625±1.866. Working that out, we get -0.30 and 3.4285. The negative root is nonsense in this case but the ball will land almost 3.5 seconds after you throw it.
That’s 3.48 (about) and the square root is about 1.866. The roots, then, are 1.5625±1.866. Working that out, we get -0.30 and 3.4285. The negative root is nonsense in this case but the ball will land almost 3.5 seconds after you throw it.
If you don’t trust our work, ask Wolfram Alpha or plug 3.4285 back into the original formula. Wolfram says 3.43 and the check your own work says 0.005 meters at that time, so given that I rounded a few times, that’s pretty close. Besides, I’m ignoring things like air resistance. This specific calculator says 3.36 seconds, which is still pretty close.
In Summary
If you prefer things in algorithmic steps, here you go:
- Find A, B, and C for the quadratic equation.
- If necessary, divide by A so that A now is 1.
- Write
-(B/2)2-z2=C - Solve for z (since you know B and C)
- Roots are
-B/2±z
Everything Old is New Again
We get it. Many people may have figured this out before. But if they did, they apparently forgot to share it with anyone in any permanent form. If you read the actual paper, you’ll see how easy it is to symbolically derive the “old” standard formula. Compare that to the traditional method. If you read the proof, it seems simple enough, but go back in a few weeks and try to work it out yourself. Not so easy. This is also much easier to remember even if you don’t want to derive it every time.
Of course, making A=1 is part of the trick. It is well known, for example, that the product of the roots of a quadratic is C/A. Since we know A=1, it follows that the product of S and R are also C, using this method. Normalizing A to 1 is also an old trick and is sometimes called a reduced quadratic equation. However, it doesn’t look like anyone put all the pieces together until now.
If you don’t like Wolfram Alpha, there’s always Mathics (hint: use Solve[-4.8t^2+15t+5==0,t]). There are also specific calculators. Or just bite the bullet and keep everything in a Jupyter Notebook.

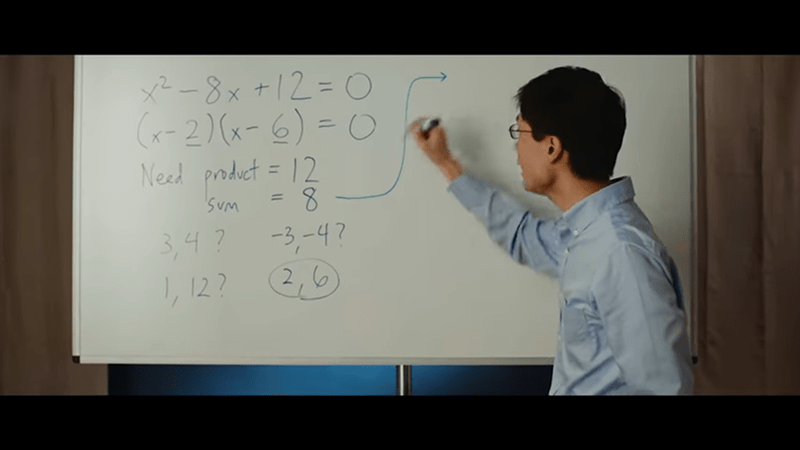













I feel like I turned this in on a math test once and got it back with a big red ink 0 and WHY??? and WHERE DID THIS COME FROM ??? and USE THE FORMULA !!! at the end, with an ensuing discussion of “But I got the right answer!”, “Not the right way, it must have been a fluke.”
(Man was I terrible at remembering formulas, I was always deriving from basics, occasionally I remembered the right symbols and so just got red pen scratch through all the working and marks from the formula on down, but should I have forgotten that I should have been using a theta and wrote Angle L or something, nil points)
My statistics professor wasn’t such a stick in the mud. I didn’t memorize any of the formulas in that class, and had to re-derive everything on the final. Took hours, but I was given full credit. If I had to do it again, I’d just memorize the formulas, though. That was a stressful test.
Helping my step-son with math is annoying, though. His professor doesn’t give partial credit. Lazy teachers…
I thought I was the only one that tried to derive from basics in an exam. :) A lot of scientists, mathematicians spent months or years on complex formulas that one would have to come up with in 15 minutes/question. :P
I like hard exams because it means remembering formulas or drilling on textbook exercises won’t help everyone else. Original ideas in hacking is about solving problems in new ways, not something from textbook exercises or copy/paste.
Reminds me when I went back to school after 25 years. I had to retake chemistry. The professor wanted the math to be done the newest way being taught. I could have done it in one or two steps but ended up having to take up a page to satisfy the requirements.
Great article, but the gravity part is wrong
If gravity accelerates things at -9.8 m/s2, that means every second, the object’s speed towards the center of the Earth increases by 9.8 m/s2. The term (at^2)/2 represents the distance the object would travel in time t during a free fall.
“Gravity is going to pull down on the ball at about 4.9 meters per second squared (assuming gravity accelerates at -9.8 m/s2). The physics formula is (at2)/2 so we get our first term of -4.8t2.” – formula is correct, but the description is wrong
That one sentence confused the bejesus out of me. I thought it was wrong. Thanks for confirming.
But the ball would have to land at the same altitude at which it left your hand…
B^)
I’m not really sure what you mean, but I’ll try to explain more and hopefully that answers your problem.
In my comment, the only formula present is for free fall: how far below the starting point will the object fall in time t assuming it doesn’t hit the ground first (that’s why you offset it by the other two terms).
Then there is the second term (vt) – distance traveled with speed v in time t. And I just realized its description in the article is wrong too (“The second term will represent the speed of the ball which is simply 15t.” – it represents distance again, not speed).
The last term is simply h – initial height / distance from ground. That is probably self explanatory.
When you add these terms up, you end up with a formula describing how high above ground will the object be at time t. If you solve (this formula) = 0, you get a time t at which you hit ground.
t is not “the time at which it hits the ground” it is “the time it takes to return to the altitude at which it was released” which is a few feet above ground level.
Sorry — missed the “h” offset. You’re right.
“FOIL (First/Inner/Outer/Last)” – Foiled again!
I’m sure I’ve seen this in a math textbook or a wikipedia article. In fact, the wikipedia article presents a more complete formula:
https://en.wikipedia.org/wiki/Quadratic_equation
> a quadratic equation has always two roots, if complex roots are considered, and if a double root is counted for two. If the two solutions are denoted r and s (possibly equal), one has
ax^2 +bx + c = a(x -r)*(x – s)
It seems trivial to note that solving for r and s results in the roots.
further down the article:
“For most students, factoring by inspection is the first method of solving quadratic equations to which they are exposed.[2]:202–207 If one is given a quadratic equation in the form x2 + bx + c = 0, the sought factorization has the form (x + q)(x + s), and one has to find two numbers q and s that add up to b and whose product is c (this is sometimes called “Vieta’s rule”[3] and is related to Vieta’s formulas). As an example, x2 + 5x + 6 factors as (x + 3)(x + 2). The more general case where a does not equal 1 can require a considerable effort in trial and error guess-and-check, assuming that it can be factored at all by inspection. ”
So this method is in fact called “Vieta’s rule” and it’s been known for ages.
Yes, as shown at the end of the video, Vieta’s Rule. The author is mostly puzzled (as am I) about why this is not taught as standard practice.
As far as I can tell, it is.
I taught high school math for 5 years from 2002 to 2007. The “modern” texts are crazy about FOIL and factoring. Teaching these days is all about “group cooperative activities”. And everyone factoring and guessing fits that idiotic model.
I for one welcome our groupthink overlords…
No seriously, I hope in about 20 years there will a huge decline in adversarial politicking and more working towards solutions.
We did the “completion of squares” derivation of the the quadratic formula in HS (~75)
I think that I agree that this method is an easier-to-see derivation, but I don’t think the final formula is any easier to remember than the “normal” form (and it has that extra “divide by A” step!)
And “easier to memorize” usually trumps “easier to understand.”
(now, it does seem like a useful technique for factoring binomials, although I’m not sure that that has an application other than a path to finding roots…)
https://www.youtube.com/watch?v=3sOSIFLHz-s
“There’s seemingly no end to how many things you can describe with a quadratic equation.”
just imagine how many things you can describe with the fourier series :)
Essentially it is the reverse of a slightly extended version of Horner’s method…
The insight used in this method–setting U as halfway between the two roots such that U+z and U-z give the roots–was described by Jim Loy on his site almost twenty years ago. His site is now gone, but an archived copy is hosted on the Wayback Machine: https://web.archive.org/web/20020118174935/http://www.jimloy.com/algebra/quad.htm
Thank you for sharing this reference! It is helpful to have a specific written version to look at, because details are important. It is great to see that Jim Loy thought of reasoning about a number halfway between the roots. As mentioned in the original article (https://arxiv.org/pdf/1910.06709.pdf), it would be very surprising if this pedagogical approach had eluded human discovery.
That said, the approach you linked above has a mathematical issue, in that although the answers it produces happen to be correct, its logic starts by requiring the fact that every quadratic x² + Bx + C definitely has a factorization into a product (x − m)(x − n). That (true) mathematical fact is typically proven by completing the square or by the quadratic formula, but that would defeat the purpose of trying to come up with another independent method that avoids completing the square. Indeed, before learning a general solution to quadratic equations, it is not at all clear to students that x² + 1 can be factorized, and indeed, the factorization would involve imaginary numbers.
Because this logical detail is easily missed, I had written an explanation of what is logically dangerous about requiring the fact of existence and making forward deductions (starting with a system of equations, using substitution, and writing line after line of equations until there is only one option left for each variable): https://www.poshenloh.com/quadraticlogicexist Within that explanation, both “Solution” 1 and “Solution 2” use the logical style in your comment (substitution, followed by stacks of equations), but mysteriously “Solution 2” produces an answer which is incorrect.
So, while Jim Loy has indeed found something nice, in order for it to be logically sound he would need to prove the mathematical fact that there definitely exist m and n which allow his factorization to complete. That fact is not obvious, and typically requires an alternative proof of the quadratic formula in order to derive, making the method not self-contained. The same issue holds for any method which relies on Viète’s Relations (suggested by other comments in this discussion area). Actually, the reason why Viète’s Relations are typically taught after the quadratic formula is because they require the knowledge that every quadratic has two roots. Often, Viète’s Relations for quadratics are proven by using the quadratic formula’s two roots and adding and multiplying them together. So, it would be circular logic to start with Viète’s Relations and deduce the quadratic formula. Instead, the approach in this article is careful to use only the converse of Viète’s Relations, which does not have any fancy name. It’s just expanding brackets, also known as the “distributive property” or “FOIL”.
If you watch (https://youtu.be/XKBX0r3J-9Y) or read (https://www.poshenloh.com/quadraticdetail) the explanation of the method described in this article, you can see that care is taken to explain how logic flows from subsequent statements backward to previous statements. That way, it is ultimately proven that the factorization exists, and no advanced existence fact is required at the outset.
Ultimately, what makes a method usable or unusable is whether it is logically sound. If a method sometimes works and sometimes fails (such as the “Solution 1” and “Solution 2” in the link above), then it is unsafe to use. What makes this method legitimate to use for beginning Algebra students is the fact that every step of it is logically established without relying on advanced mathematical facts. The logic is straighforward enough that the answer to the question “why can you do this?” is clear in each step. That is what sets it apart from prior work such as the article of Jim Loy linked above.
Hm. Vieta’s formulas [1], after François Viète, 1540-1603 [2]
No Fields medal for you this time.
[1] https://en.wikipedia.org/wiki/Quadratic_equation#Vieta's_formulas
[2] https://en.wikipedia.org/wiki/Fran%C3%A7ois_Vi%C3%A8te
“in this case, A=1, B=6, and C=3” should be B= -6?
(—6)*x, so B=(-6)
Negative root isn’t nonsense. Just means that following the same trajectory and gravity backwards, the ball would have left the ground 0.3 seconds ago.
If you imagine we froze the ball mid-bounce instead of throwing it, and asked when will the ball hit the ground again and how long since it last bounced, the meaning of the roots is more intuitive.
Al: “FOIL (First/Inner/Outer/Last)”
F – First
O – Inner
I – Outer
L – Last
And I’m reading the rest of the article because…?
Nothing new to see here
something something common core math.
Btw there is a cubic equation too. Back in high school, I wrote polynormal solver program in BASIC that uses Newton’s method. Once a root is found, it divide the poly and solve until it drop down to cubic/quadratic equations.
Those were fun times before graphing calculators with solver packages and I learnt a lot than from school.
Science used to be at a somewhat slower pace in ancient times.
A fun example is the concept (and later creation) of vacuum:
https://en.wikipedia.org/wiki/Vacuum
(quote)
There was even speculation that even God could not create a vacuum if he wanted and the 1277 Paris condemnations of Bishop Etienne Tempier, which required there to be no restrictions on the powers of God, which led to the conclusion that God could create a vacuum if he so wished.
(/quote)
I guess Einstein is lucky he didn’t end up boiled in oil for telling God he’s not allowed to play dice.
I think step 3 in summary should be (B/2)² – z² = C. As in embedded YouTube 3:11.
I really do not understand what is new in this, this is how we were taught to find roots in school in India
Seems like just the way we learn it over here :)
https://de.wikipedia.org/wiki/Quadratische_Gleichung#L%C3%B6sungsformel_f%C3%BCr_die_Normalform_(p-q-Formel)
There is nothing new here. The symmetry comes from the geometry. Plot a parabola: it has a minimum or a maximum. The roots are the places where it crosses the axis, symmetrically located about the extremum. If the parabola does not cross the axis, then you have complex roots.
Honestly, educators are ruining mathematics. FOIL?? what nonsense. It does nothing but confuse and betrays an ignorance of the fundamentals of arithmetic by reducing them to idiotic ritual. What has the world come to when a Carnegie Mellon mathematician can be recognized for rediscovering something that should not have been forgotten in the first place and then proceeds to once again eradicate the geometry and ritualize the process. Twenty thumbs down.