Quantum computers stand a good chance of changing the face computing, and that goes double for encryption. For encryption methods that rely on the fact that brute-forcing the key takes too long with classical computers, quantum computing seems like its logical nemesis.
For instance, the mathematical problem that lies at the heart of RSA and other public-key encryption schemes is factoring a product of two prime numbers. Searching for the right pair using classical methods takes approximately forever, but Shor’s algorithm can be used on a suitable quantum computer to do the required factorization of integers in almost no time.
When quantum computers become capable enough, the threat to a lot of our encrypted communication is a real one. If one can no longer rely on simply making the brute-forcing of a decryption computationally heavy, all of today’s public-key encryption algorithms are essentially useless. This is the doomsday scenario, but how close are we to this actually happening, and what can be done?
The Threat to Classical Encryption
To ascertain the real threat, one has to look at the classical encryption algorithms in use today to see which parts of them would be susceptible to being solved by a quantum algorithm in significantly less time than it would take for a classical computer. In particular, we should make the distinction between symmetric and asymmetric encryption.
Symmetric algorithms can be encoded and decoded with the same secret key, and that has to be shared between communication partners through a secure channel. Asymmetric encryption uses a private key for decryption and a public key for encryption onlytwo keys: a private key and a public key. A message encrypted with the public key can only be decrypted with the private key. This enables public-key cryptography: the public key can be shared freely without fear of impersonation because it can only be used to encrypt and not decrypt.
As mentioned earlier, RSA is one cryptosystem which is vulnerable to quantum algorithms, on account of its reliance on integer factorization. RSA is an asymmetric encryption algorithm, involving a public and private key, which creates the so-called RSA problem. This occurs when one tries to perform a private-key operation when only the public key is known, requiring finding the eth roots of an arbitrary number, modulo N. Currently this is unrealistic to classically solve for >1024 bit RSA key sizes.
Here we see again the thing that makes quantum computing so fascinating: the ability to quickly solve non-deterministic polynomial (NP) problems. Whereas some NP problems can be solved quickly by classical computers, they do this by approximating a solution. NP-complete problems are those for which no classical approximation algorithm can be devised. An example of this is the Travelling Salesman Problem (TSP), which asks to determine the shortest possible route between a list of cities, while visiting each city once and returning to the origin city.
Even though TSP can be solved with classical computing for smaller number of cities (tens of thousands), larger numbers require approximation to get within 1%, as solving them would require excessively long running times.
Perfect Forward Secrecy
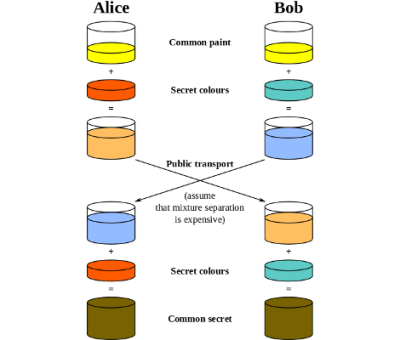
Symmetric encryption algorithms are commonly used for live traffic, with only handshake and the initial establishing of a connection done using (slower) asymmetric encryption as a secure channel for exchanging of the symmetric keys. Although symmetric encryption tends to be faster than asymmetric encryption, it relies on both parties having access to the shared secret, instead of being able to use a public key.
Symmetric encryption is used with forward secrecy (also known as perfect forward secrecy). The idea behind FS being that instead of only relying on the security provided by the initial encrypted channel, one also encrypts the messages before they are being sent. This way even if the keys for the encryption channel got compromised, all an attacker would end up with are more encrypted messages, each encrypted using a different ephemeral key.
FS tends to use Diffie-Hellman key exchange or similar, resulting in a system that is comparable to a One-Time Pad (OTP) type of encryption, that only uses the encryption key once. Using traditional methods, this means that even after obtaining the private key and cracking a single message, one has to spend the same effort on every other message as on that first one in order to read the entire conversation. This is the reason why many secure chat programs like Signal as well as increasingly more HTTPS-enabled servers use FS.
It was already back in 1996 that Lov Grover came up with Grover’s algorithm, which allows for a roughly quadratic speed-up as a black box search algorithm. Specifically it finds with high probability the likely input to a black box (like an encryption algorithm) which produced the known output (the encrypted message).
As noted by Daniel J. Bernstein, the creation of quantum computers that can effectively execute Grover’s algorithm would necessitate at least the doubling of today’s symmetric key lengths. This in addition to breaking RSA, DSA, ECDSA and many other cryptographic systems.
Quantum Computers Today
The observant among us may have noticed that despite some spurious marketing claims over the past years, we are rather short on actual quantum computers today. When it comes to quantum computers that have actually made it out of the laboratory and into a commercial setting, we have quantum annealing systems, with D-Wave being a well-known manufacturer of such systems.
Quantum annealing systems can only solve a subset of NP-complete problems, of which the travelling salesman problem, with a discrete search space. It would for example not be possible to run Shor’s algorithm on a quantum annealing system. Adiabatic quantum computation is closely related to quantum annealing and therefore equally unsuitable for a general-purpose quantum computing system.
This leaves today’s quantum computing research thus mostly in the realm of simulations, and classical encryption mostly secure (for now).
A Quantum Future
When can we expect to see quantum computers that can decrypt every single one of our communications with nary any effort? This is a tricky question. Much of it relies on when we can get a significant number of quantum bits, or qubits, together into something like a quantum circuit model with sufficient error correction to make the results anywhere as reliable as those of classical computers.




At this point in time one could say that we are still trying to figure out what the basic elements of a quantum computer will look like. This has led to the following quantum computing models:
- quantum gate array (quantum gates)
- one-way quantum computer (one-qubit measurement series)
- adiabatic quantum computer (see quantum annealing)
- topological quantum computer (braiding of anyons in a 2D lattice)
Of these four models, quantum annealing has been implemented and commercialized. The others have seen many physical realizations in laboratory settings, but aren’t up to scale yet. In many ways it isn’t dissimilar to the situation that classical computers found themselves in throughout the 19th and early 20th century when successive ‘computers’ found themselves moving from mechanical systems to relays and valves, followed by discrete transistors and ultimately (for now) countless transistors integrated into singular chips.
It was the discovery of semiconducting materials and new production processes that allowed classical computers to flourish. For quantum computing the question appears to be mostly a matter of when we’ll manage to do the same there.
A Quantum of Encryption
Even if in a decade or more from the quantum computing revolution will suddenly make our triple-strength, military-grade encryption look as robust as DES does today, we can always comfort ourselves with the knowledge that along with quantum computing we are also increasingly learning more about quantum cryptography.
In many ways quantum cryptography is even more exciting than classical cryptography, as it can exploit quantum mechanical properties. Best known is quantum key distribution (QKD), which uses the process of quantum communication to establish a shared key between two parties. The fascinating property of QKD is that the mere act of listening in on this communication will cause measurable changes. Essentially this provides unconditional security in distributing symmetric key material, and symmetric encryption is significantly more quantum-resistant.
All of this means that even if the coming decades are likely to bring some form of upheaval that may or may not mean the end of classical computing and cryptography with it, not all is lost. As usual, science and technology with it will progress, and future generations will look back on today’s primitive technology with some level of puzzlement.
For now, using TLS 1.3 and any other protocols that support forward secrecy, and symmetric encryption in general, is your best bet.















“Grover’s algorithm would necessitate at least the doubling of today’s symmetric key lengths.”
That’s true for 128 bit keys, but a 256 bit key with a competent symmetric cipher still gives adequate security for most applications even assuming a worst case future.
Offhand, I can’t think of any applications that don’t already support 256 bit keys.
At least one common model of TPM supports only up to 128-bit AES for symmetric ops as far as I can tell. Most don’t support bulk symmetric operations so it’s hard to check.
“Asymmetric encryption uses a private key for encryption and a public key for decryption only. This enables public-key cryptography: the public key can be shared freely without fear of impersonation because it can only be used to decrypt and not encrypt.”
That’s backwards. Public key is for encrypting and private is for decrypting.
It’s kinda forwards for signing and I’ve always wondered about that.
+1 :)
That’s the magic of the PGP system. You can encrypt with either key, and either way, the opposite key decrypts. Which key you use depends on what you’re doing.
Well said. I was going to make this point also. I hate when the experts keep explaining this wrong. If both keys couldn’t be used for encryption and decryption of the other key’s output then signatures would not be a thing.
Just so. If plaintext is crypted with the secret key then it can only be decrypted with the public key, indicating that the holder of the secret key is the only one* who could have produced the ciphertext. If plaintext is crypted with the public key then it may only be decrypted with the private key, so no one but the holder of the secret key could have produced the ciphertext. * Assuming that the secret key is not stolen. I’m an idiot and I understand this much. Are the posters above smoking crack?
That should be: ” If plaintext is crypted with the public key then it may only be decrypted with the private key, so no one but the holder of the secret key can recover the plaintext”
“Asymmetric encryption uses a private key for decryption and a public key for encryption only. This enables public-key cryptography: the public key can be shared freely without fear of impersonation because it can only be used to decrypt and not encrypt.”
Is it just me, or does it seem like those two sentences are saying the opposite on what public keys are used for?
AFAIK, the first sentence is right: public keys are used to encrypt and private keys are used to decrypt.
You can use the private key both for decrypt and encrypt, and then use the public key to do the opposite.
Just get LINUX and you are covered
no, you “can’t” encrypt anything with a private key because the public key is PUBLIC. Thus any encryption with the private key is a waste of time, energy and so on.
What you can do is sign “stuff” with your private key so everyone can verify said “stuff” cam from you by verifying “stuff”+signature against your public key.
Which IS encrypting with the private key. ;-) But, yeah, you wouldn’t encrypt private stuff with the private key and throw it out “there”.
You are confusing the terms “encoding” and “encrypting”
“Encoding” means to manipulate data in a way that is reversible. This is what the math does.
“Encrypting” is encoding for the purpose of maintaining confidentiality.
“Signing” is encoding for the purpose of verifying identity.
Encoding with a private key means everyone (as everyone can have the public key) is able to decode it. There is no form of confidentiality there, so isn’t encrypting.
Same thing. Signing is done by encryption using a private key, so you have just given an example where it’s not a waste of time.
The “public” key could be distributed to a closed user group only, not so public I suppose. “CLUBLIC”?
This is why the two keys are actually named “q” and “p”, they are complements of each other but have no inherent distinction. It is us humans that designate one as private and one as public.
Using a public key to encode and private key to decode is called “encryption”
Using a private key to encode and public key to decode is called “signing”
Both rely on the assumption that the private key is only held by the key-pair maker.
Thus encoding with the public key ensures only the private key holder can decode the data, and encoding with the private key ensures everyone else only the private key holder could have generated that data.
In practice, it is a good idea to do both of those together.
Encrypt the data with a public key to ensure only the recipient can decode it, and encode that with your private key to ensure the recipient who it was that sent it.
(Of course “who” actually refers to a key-pair, it is also an assumption a key-pair is linked to a person)
Time to dump those bitcoins!
I woulddn’t rush. One thoughtful forking with new encryption, a transfer of all wallets to new wallets and they are golden. Remember such cryptocurrency projects are not static. They are maintained and alive, the viable ones anyway. But, alas, Dogecoin is dead :-(
Awwww not doge… I’ve got 2000 somewhere I was waiting until they were worth a penny LOL
I’d love to see an article here on how they achieve the near zero K operating temperatures and how that is implemented. Also looking at the D-Wave article on wikipedia the power consumption is insane. 25 kW. One can surmise these may never be consumer products.
My car is 180kW…
Two words: Mr. Fusion. :)
lol not one but two technologies that may never mature!
Fine, when turbines get cheap, I’ll run it from my personal home turbine generator that runs off piped in hydrogen.
“Extremely low temperatures” effectively refers to the temperature of the *states*, not necessarily the temperature of the *system*. You want the state population to effectively be only controlled by you, which means that if you would compute the temperature, they’re as close to zero-K as you can get.
Many quantum computing designs do use system temperatures near zero, but there are several that don’t need them. In general the idea is that you just engineer the material such that the states you’re interested in are isolated and trapped. Those designs are basically all conceptual at this point because it doesn’t really make practical sense to go after them – cooling things down to near absolute zero is easy.
“Also looking at the D-Wave article on wikipedia the power consumption is insane. 25 kW. One can surmise these may never be consumer products.”
Really? Wouldn’t one have surmised that ENIAC would never be a consumer product either, then? It pulled 160 kW.
Depends on if it’s particularly useful to have one. That’s about the same power draw as a tankless water heater.
Oh, come on, that’s just about 20 electric kettles. Not that hard to imagine, right? ;-)
Interestingly, quantum computing may bring trapdoor knapsack cryptosystems back to life. I cut my teeth on those in the early 80’s, but they’ve been broken since the late 80’s. A modification (e.g. ‘Nasako-Murakami’, 2006) makes them secure again, and quantum resistant.
https://www.researchgate.net/publication/220334596_Knapsack_Public-Key_Cryptosystem_Using_Chinese_Remainder_Theorem
Excellent remark!
Thanks for the link.
Will this affect Enigma?
a) Enigma is a symmetric cipher, and does not depend on prime factorization, which is the fundamental thing at risk here.
b) Enigma was compromised long ago, and should not be used today. But you knew that.
It’s a sad fact that we know for sure that quantum computers will be mostly used to break encryption.
This is one of the very rare times that majority of people agree on how a new technology will be used.
I don’t know if it’s because we became more aware about the lack of ethics in companies and governments forgot it’s job or I don’t know what else could be but I don’t see enough articles or discussions focusing on the uses of quantum computing in science for example like how most articles about the current supercomputers.
It’s sad that we are more worried than excited.
nil desperandum, amicus! I suspect the apparent focus on breaking (asymmetric) encryption is simply that it is a fairly obvious application, easy to discuss, and represents an immediate threat to be addressed. But the researchers are definitely at work with other, perhaps more uplifting, applications. E.g., q.v.
https://builtin.com/hardware/quantum-computing-applications
Breaking crypto will be just a tiny fraction of applications and certainly not the most important one.
Simulating physical processes with impact to material science (think: better batteries, new materials, new chemicals, new drugs) is really the ultimate trophy that will give instant civilizational advantage to the winner in the quantum computing race.
What a hot mess. The writer of this article really needs to read this https://en.wikipedia.org/wiki/Quantum_complexity_theory more carefully. Factorization is a very special case as it is NP, but not known to be NP-complete. There are plenty of other public encryption systems that don’t use factorization (or things that are mathematically equivalent).
Quantum computers, assuming P≠NP, don’t help with NP complete problems.
But what if they can guess at the unguessable 10 times faster eh?
This seems overexaggerated. There are already some quantum-computing-resistant asymmetric cryptographic algorithms which at least exist (like “ring learning with errors”, apparently), and doubling symmetric key length, while possibly problematic for some stuff and somewhat bad for performance, is not bad enough for it to cause “the end of encryption”.
Indeed, you get worried when they throw around quotes like talking several powers of ten off the time required, but when time required was “until the heat death of the universe” with Moores law implied, a few powers of ten off that is still many millions of years.
You should probably only worry right now, if you were using something expected to be broken “in about 10 years” you should worry next week sometime if it was a 100 years off, and take a while to think about it and see where things are going if it was 1000. If it was 10,000 or more, you’re probably good for a decade at least.
Security is mostly an economic problem.
It will make a big difference if the Quantum Computer costs $10 or $10 Billion.
There’s also steganography. You have to obtain the ciphertext to decrypt it.
Meanwhile 1Tb uSD cards are also getting cheaper and QC can’t decrypt one-time-pads.
Way back when (before Back to the Future), they were predicting flying cars. I’m still waiting.
I definitely don’t want to have to mail an SD card to every website I use.
And THAT hits the nail right on the head. The attraction of RSA and similar forms of encryption is that it is very cheap to use, and we have built a whole culture on the assumption that this will remain secure at least for our own lifetimes. The takeaway from this should be that at some point it may be possible to break all of these methods we depend on, in a retroactive way. That is, once you have put encrypted data out there in the open, there is the possibility that it has been recorded, which means that if the encryption is broken, anything you have EVER sent in encrypted form (using what will eventually be a broken algorithm) is vulnerable.
People (yarrr matey) already buy “blocks” of usenet data download in the hundreds of GB per month. Instead you could buy “secure” bandwidth that comes with a OTP shipped to you by your ISP.
I would not be surprised if in the end, linear increases in the number of qubits in a system would be able to outscale practical increases in key length, but linear increases in the number of qubits would also come with an exponential increase in system complexity, thus still making it impractical.
This kind of FUD article gives me the pip, as my dad would have put it. It’s all if this and if that, assuming that those things are likely *and* that the rest of the crypto world is going to stay still and wait for that bus. As many have said before, there’s no good reason to think that an actual quantum computer with enough qbits to be useful will be available any time soon, much less that it would be affordable or practical for mass production (those last two might be the same).
And even if that were to happen, those standards are evolving already, to be ready.
Someone could have written the same article in 1990 predicting that computers would get fast enough that DES would become trivially breakable, and OMG, what will we do then?!?! (Actually, I bet that if you dug through the ComputerWorld archives, you’d find that exact article, minus the “OMG”, which wasn’t a thing yet.)
Same answer: standards evolve, CFD.
You’re so full of “pip” you missed the good in the article, IMO.
Differently from the 90s, everything you do is being archived now for future decryption and analysis.
What can you do about it? Answer: symmetric encryption makes it significantly more challenging for quantum computers.
Yes, yes, all of that, yes. However: there is a class of information which people wish to keep secret for longer than the next decade or two. This becomes a problem if ten years ago, a bunch of stuff was encrypted and distributed using what was then thought to be secure for at least, let’s say, a hundred years. But the nagging doubt about methods based on products of large prime numbers has always been, what if some new technology breaks the underlying assumption, that it is difficult to find the prime factors of very large numbers? Now we have a candidate for such a potential game-changer, so even if nobody has demonstrated this actual capability, the potential for it is what has to be considered in long-term security planning. If encrypted information distributed years ago was recorded in its encrypted form, there is always the possibility that it can be decrypted using technologies not available when it was originally distributed. So the problem isn’t how to be secure starting from today, but how secure information from the past is.
And now I see that Elliot said this much more succinctly. Never mind.
You know, I’ve heard that “everything is archived” but I’ve never seen anything supporting the claim. Feels more like marketing hype for some product than reality. Plus most information *value* has a very limited shelf life.
And archives are also stored with other protections, so the value of attacking them even if you thought you could decrypt them seems low. Not impossible, but not a major threat vector.
So…I’m unconvinced that archives encrypted with symmetric encryption represent any significant threat to anyone.
That is of course your choice. Most people I know who are entrusted with information whose value a) is high, and b) depends on controlling access to it, take a more serious approach than “hey, it ought to be all right – it’s not like anybody is trying to steal our secrets”.
Heh. Not what I said, but cute.
Summary:
1. Grover’s weakens AES-256, but only to about AES-128, so it’s still secure.
2. Shor’s could (if they ever actually made a quantum computer) could crack key exchange algorithms such as Elliptic-Curve Diffie-Hellman. Fortunately, there are already post-quantum key exchange algorithms (e.g., McEliece) that can replace ECDH. Yes, they are a little more inconvenient, but they are there.
3. Quantum Key Distribution is completely unnecessary. It’s fragile, complex, and not required because of #1 and #2.
Yup.
Interesting article that was been written over the many years since quantum computers became a things. When is the key word. Not saying we should do nothing however I would not worry to much until this type of computing able to do something meaningful.
This article so confusing! Is there anyone doing reviews of articles before they appear on hackaday?
> “Here we see again the thing that makes quantum computing so fascinating: the ability to quickly solve non-deterministic polynomial (NP) problems”
Quantum computers do not offer ability to solve ALL NP problems. In particular, NP-complete problems are not easily solved by quantum computers. What makes them exciting is the ability to solve *some* problems that are believed to be beyond P, like integer factorization or discrete logs.
> ” NP-complete problems are those for which no classical approximation algorithm can be devised.”
This is not true. NPC class is a class of NP problems X such that all other problems in NP are polynomial time reducible to X. It has nothing to do with approximations. Some NPC problems have good approximation algorithms, some don’t. Traveling Salesman Problem is an example of a problem that has good approximation algorithms.
Section on Perfect Forward Secrecy is completely confusing. Session encryption always uses symmetric keys (since symmetric algorithms are much more efficient). The difference is how those symmetric session keys are established. We can e.g. encrypt them with long-term asymmetric keys before sending to the other party — then breaking of the long-term key indeed reveals all the previous session keys. Alternatively, we can use ephemeral key establishment process (like Diffie-Hellman) to get one-time keys.
However, quantum computers can easily break discrete logarithms, so from the recorded session traffic an attacker could recover those session keys anyway. From the point of view of quantum adversaries perfect forward secrecy does not matter as long as it uses quantum-breakable key establishment like DH. This section is therefore irrelevant for the overall discussion of quantum attacks.
Quantum Key Distribution is not necessary to achieve security against quantum computing adversaries. The whole area of so called “post-quantum cryptography” is concerned with designing classical asymmetric algorithms that resist quantum attacks. Examples of such algorithms include hash-based signatures like XMSS, cryptosystems based on coding theory like dating back to ’70 McElice and newer ones based on lattices. National Institute of Standards and Technology is actually running a competition for new, post-quantum algorithms that will replace RSA and DH.
> “For now, using TLS 1.3 and any other protocols that support forward secrecy, and symmetric encryption in general, is your best bet.”
Again, forward secrecy with Diffie-Hellman does not protect you against quantum adversaries. However, simple search for “TLS post-quantum” will show you that many Internet companies are experimenting with post-quantum ciphersuites for TLS (from the above-mentioned NIST competition) so you can already have experimental support for them in some of the browsers.
TL;DR: 1/ Don’t trust this article too much; 2/ Cryptographers will replace vulnerable algorithms with quantum-resistant ones before quantum computers get large enough to break current RSA and EC-based crypto.
Quantum Encryption.
I think they mean CLASSIC and NOT Classical.