Mathematical transforms can be a great help in understanding signals. Imaging trying to look at a complex waveform and figuring out the frequency components without the Fourier transform. [Artem Kirsanov] calls the wavelet transform a “mathematical microscope” and his video gives you a great introduction to the topic. You can see the video below.
The video starts with a discussion about how the time domain and frequency domain have a dual relationship — not big news if you’ve dealt with Fourier transforms and — in fact — that’s the next topic in the video. However, there are limitations to the transformation — you lose time domain information in the process.
Obviously, the wavelet transform can address these limitations. The transform is similar to applying Fourier, but instead of decomposing to a series of infinite sine waves, wavelet transformation decomposes signals into finite functions that meet certain conditions.
You do need a little math to follow the video, but probably not as much as you might think. The explanations are clear and there are few assumptions about your prior knowledge. If you’ve encountered windows in Fourier analysis, the ideas are somewhat similar.
If you want to experiment with some DSP concepts in a spreadsheet, you can do that. If you don’t intuitively grasp the Fourier transform, try watching [3blue1brown’s] enlightening video on the topic.

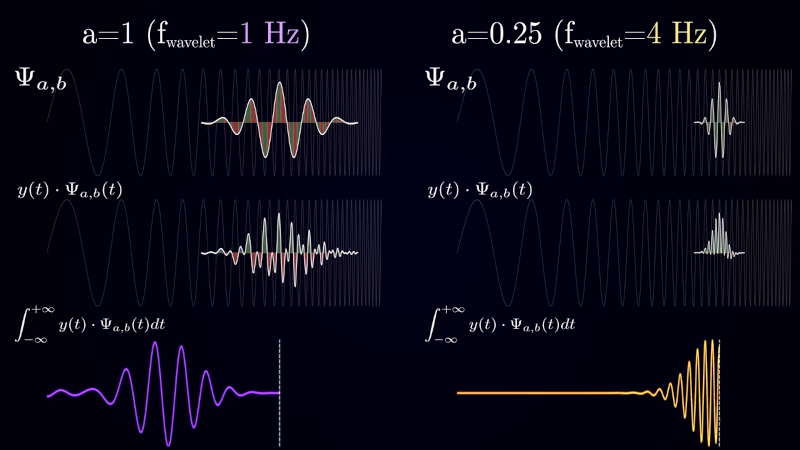















Very clear description of the subject. I’m not sure where I would use the subject material, but now at least I have a chance.
Yeah, I’m not sure either. Except for my waterfall frequency display, kids disco light setup, stock trade analysis, engine failure prediction, fuel consumption estimation.. just off the top of my head.
As to the video, it does a really great job explaining a topic a lot of folks have a hard time wrapping their heads around. (I certainly did back in the day.)
When I explain it, I like to start kind of in the middle showing how to extract specific frequency responses first, as this is the one most people struggle with and having it out of the way first helps. Only then do I work my way back to the topics shown early in this video, and finish with the rest.
one application is blob detection in image processing, like a band pass filter but for blob sizes
I tried it once for barcode detection, but turned out to be too slow in comparison to alternatives.
Sounds a bit like what you would do when obtaining spectrograms.
They are closely related. The main difference (that I heard anyway), spectograms use a fixed window, where as wavelets vary the window size. I.e. lower frequencies get bigger windows since they take longer (longer period), and higher frequencies get smaller windows since they will have a shorter period.
+1
Are Wavelets actually used anywhere with an advantage over windowed Fourier Transformation? I studied applied mathematics and used Wavelets multiple times, but I never really had the impression they were better then just using windowed FT. If you really have a multi-scale problem with features or noise or something you want to extract/remove on multiple levels, Wavelets might be easier to use. But I don’t remember them being used to any benefit in productive environments.
Sure JPEG2k uses them (and Cinema DCPs with that), but Jpeg2k never really had any great benefit over Jpeg that really came from the Wavelet technology. And 20 years later new codecs are still using DCT-like technology, because Wavelets just didn’t prove useful.
Thinking about it a bit, todays Image/Video codecs use multiple different block sizes. So they also have some multiscale analysis using only the DCT.
I don’t want to say Wavelets, especially their multiscale analysis is useless. I just never saw a good application for it. Wikipedia also mainly states image compression and denoising. And there is Wavelet OFDM, but it is only used for some powerline transmission standard…
(I’m mainly talking about the DWT. CWT probably has some applications in Mathematics and theoretical physics.)
One of my favorites was using them for analyzing aspects of stock trades where certain cases were handled far better than with alternatives. In the end I tossed the approach entirely, but it was an interesting exercise that definitely exposed information that was otherwise not readily apparent.
@Mike said: “Are Wavelets actually used anywhere with an advantage over windowed Fourier Transformation? I studied applied mathematics and used Wavelets multiple times, but I never really had the impression they were better then just using windowed FT.”
Wavelets excel in what is called “multi-resolution analysis”. The wavelet transform has the ability to identify frequency (or scale) components, simultaneously with their location(s) in time. Plus wavelet transforms are generally faster than a more generalized approach like the windowed Fourier transform. Fourier transforms deal with just two basis functions (sine and cosine), while there are an infinite number of wavelet basis functions.
Wavelets are also very good at compression when the corpus of target data is bounded by certain characteristics that are well suited to the selection of a “mother wavelet” and her related child wavelets. For example the FBI takes this approach with wavelet coding to store fingerprints.
This is explained further in Section 2.12, “Transforms/Wavelets” in the U.S. Navy’s 2013 455-page “Electronic Warfare and Radar Systems Engineering Handbook”, which is approved for
public release and may be freely downloaded as a .pdf.[1][2]
* Reference:
1. Electronic Warfare and Radar Systems Engineering Handbook
https://www.microwaves101.com/encyclopedias/ew-and-radar-handbook
2. Electronic Warfare and Radar Systems Engineering Handbook [4,293 KB Download]
https://www.microwaves101.com/uploads/ElectronicWarfareandRadarSystemsEngineeringHandbook2013.pdf
I’m working on an audio generation project where wavelets might have applications. Part of it involves taking instrument samples and extracting data that can be used to synthesize them, and I suspect this has significant potential for handling tonal changes in an instrument over time (like the initial pluck sound of a guitar string that only occurs very early then fades into just the string vibration). Maybe windowed FT would accomplish the same thing, but I suspect wavelets could get better precision. Also, they might even be cheaper to store, which is important, as one of my applications for this is an embedded device with limited storage. Of course, there’s also potential for using this to create completely new synthetic sounds more elegantly, which is a major part of the project as well.
I guess we will see. This is highly experimental work, and I don’t have as much experience with advanced audio synthesis, so there’s probably going to be a lot of trial and error.
There used to be a software called “sonicWORX” that had all sorts of wavelet based sound processing algorithms in the early 90s. Will probably run on SheepShaver or any other classic MacOS 9 emu. Need to dig out the install CD sometimes soon…
This video is truly excellent and well prepared. I may give it to my students in a graduate course in quantum mechanics. One small issue, however, the function the presenter uses does NOT actually satisfy the admissibility condition he states.
Wavelets were/are practically applied for peak deconvolution in cheminformatics.
Wavelet Analysis is very important and interesting in Applied Mathematics and Industrial Mathematics especially in Mathematical Modelling. A very brief description given here. Wavelet Analysis is properly studied in Partial Differential Equations courses.
Could this be used to transform algorithms like Bitcoin mining into waves, and run them through a noise canceling FPGA to get the answer? Like analog computing.🤔