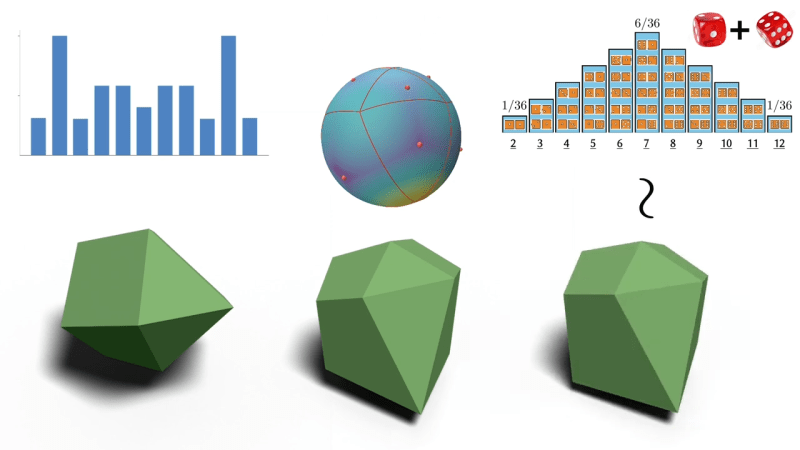
Rolling two six-sided dice (2d6) gives results from 2 to 12 with a bell curve distribution. Seven being the most common result, two and twelve being the least common. But what if one could do this with a single die?

As part of research Putting Rigid Bodies to Rest, researchers show that a single eleven-sided asymmetric shape can deliver the same results. That is to say, it rolls numbers 2 to 12 in the same distribution as 2d6. It’s actually just one of the oddball dice [Hossein Baktash] and his group designed so if you find yourself intrigued, be sure to check out the 3D models and maybe print your own!
The research behind this is a novel method of figuring out what stable resting states exist for a given rigid body, without resorting to simulations. The method is differentiable, meaning it can be used not just to analyze shapes, but also to design shapes with specific properties.
For example, with a typical three-sided die each die face has an equal chance of coming up. But [Hossein] shows (at 8:05 in the video, embedded below) that it’s possible to design a three-sided die where the faces instead have a 25%-50%-25% distribution.
How well do they perform in practice? [Hossein] has done some physical testing showing results seem to match theory, at least when rolled on a hard surface. But we don’t think anyone has loaded these into an automated dice tester, yet.















The “piglet standing on its snot” orientation shows pretty well that disregarding momentum HAS a significant impact on probabilities.
Exactly.
Momentum and spin has a great impact on the odds of outcomes.
The model ignores momentum, spin, elastic properties of material and surface, friction of material and surface, angle of the surface, and aerodynamics. Giving the piglet a specific spin will definitely impact the outcome. So does the type of surface (table cloth vs hard table) and it’s angle (piglet probably cannot stand on it’s nose on steep surface).
The model is a good start, but it’s the bare minimum.
A coin toss also does not depend on these parameters but only on geometry. They showed that geometry ist enough for a perfectly good prediction of the probabilities.
a pig is not a coin
a coin is symmetrical
a pig bounces around in ways where a tiny surface is not stable enough to land on in such a way that it’s odds are not proportional
Maybe if you drop an object straight down. Not if it bounces around.
Btw, a coin has three faces, so you definitely have a non-nul probably that it lands on its side, and neither heads or tails.
Rolling it off your thumb spinning is, by far, the best way to play quarters.
With a good table, you just don’t miss.
Quarters becomes like tictactoe…
What’s the point again?
Drunk girls…
Proceed…
Don’t scare them off, sandbag.
Landing on its side, just like that old Twilight Zone episode.
” Giving the piglet a specific spin will definitely impact the outcome.” This effects regular dice too. If you noticed, many dice games require some device to kill off spin (cup, horizontal distance against a wall of some type).
How to cheat at liars dice.
Shake the cup so the dice frequently stack, circular motion.
If the bottom dice in the stack are good, just tap them, if they’re not, give the cup a good shake.
I don’t do this, but an ‘Irishman’ (British American) I know who claims ‘great Irish luck’ does.
Not by accident either, he taught his kid the trick.
Watch for it.
“with a typical three-sided die”
A three sided die? At this time of the year? Located entirely inside this article?
…
May I see it?
That also caught my eye, though I remembered that a coin is actually 3-sided (with very poor odds on the 3rd, curved side). I suppose a more cylindrical coin could be even odds.
It seems the example in the video is a triangular prism, with the ends angled such that they are unstable (ie, it will always fall over if it lands on the ends).
My gut says football shape made of 3 distinct wedges like a triangular prism with the sides pinched to a point.
This is what I would classify as “knowing too much math for your own good.” This is absolutely brilliant but also entirely pointless… unless they are shooting to win the Ig Nobel Prize.
Which is a totally legit objective.
I worked on a scientific project whose sole objective in conceiving it, was to get us a summer in Antarctica. (It did).
God bless our now deceased Prof, who schooled me on the philosophy of ensuring that work works for you, and set the standard for bosses who look out for their staff’s best interest.
After watching the video, and looking at the strange list of sponsors, I immediately suspected it’d come in handy for:
– physics simulation shortcuts for game engines
– robotic handling of parts
There are similar problems that people have found transformative approximations for that now allow near real-time, interactive results where analytical solutions don’t exist.
Light transport, electro- and magnetostatics, ..
This is genius work!!!
This is useless.
What’s obviously needed is 16 sided die that emulates 3×6.
A d16 that emulates 3d6 is precisely what I came in here looking for.
But that d11 is nice for Catan.
Could be interesting to make your own, non-randomish, dice for games.
Super cool write-up. I like that they’re starting from the rigid body / stable resting states and then backing into the probability distribution instead of just simulating throws. Makes me wonder how far you could push this for custom board-game dice with weird curves, or even “loaded” dice that are only loaded by geometry. The 3-sided 25/50/25 die is exactly the kind of over-engineered little object that makes me happy.
I don’t think the distributions shown are bell shaped ( meaning ‘normal’ distribution). Maybe binomial if I remember correctly.
It’s a triangular distribution.
That’s what stuck out to me too. Definitely not a bell curve. The technical name is described here: https://en.wikipedia.org/wiki/Probability_distribution#Discrete_probability_distribution
It does not give a bell curve distribution. The sum of two uniform (square) distributions is a triangle. It’s clearly visible from the histogram that this is a triangle. Only in the limit of summing many uncorrelated random sources do you converge on a normal distribution (bell curve).
Correct – the histogram in turn simply contains the number of corresponding outcomes in a table with rows 1, 2, 3, 4, 5, 6 and columns 1, 2, 3, 4, 5, 6 where the cells are the sum of those:
2 3 4 5 6 7
3 4 5 6 7 8
4 5 6 7 8 9
5 6 7 8 9 A
6 7 8 9 A B
7 8 9 A B C
turn it by 45° and the origin of the histogram becomes obvious.
In the 3d6 case, this would turn into a plane normal to and traversing in the diagonal direction of a 6x6x6 cube, with the histogram points relating to the truncated surface areas.
Correct. The more dice throws you add the closer it gets to a bell curve. But at 2 throws it’s a triangle. It’s also discrete, not continuous, like a true bell curve. So it’s a discrete triangular distribution.
For higher number of throws it’s the discrete equivalent of the Irwin–Hall distribution