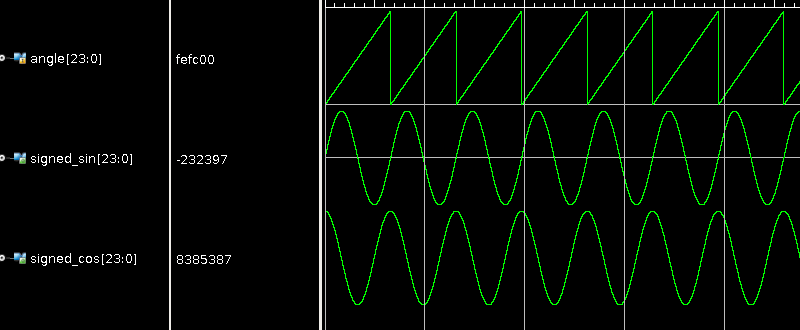
We are always excited when we see [Hamster] post an FPGA project, because it is usually something good. His latest post doesn’t disappoint and shows how he uses the CORDIC algorithm to generate very precise sine and cosine waves in VHDL. CORDIC (Coordinate Rotation Digital Computer; sometimes known as Volder’s algorithm) is a standard way to compute hyperbolic and trigonometric functions. What’s nice is that the algorithm only requires addition, subtraction, bit shifts, and a lookup table with an entry for each bit of precision you want. Of course, if you have addition and negative numbers, you already have subtraction. This is perfect for simple CPUs and FPGAs.
[Hamster] not only has the VHDL code but also provides a C version if you find that easier to read. In either case, the angle is scaled so that 360 degrees is a full 24-bit word to allow the most precision. Although it is common to compute the result in a loop, with the FPGA, you can do all the math in parallel and generate a new sample on each clock cycle.
It is actually impressive how short the VHDL code is. VHDL is fairly verbose, too, so we imagine a Verilog translation would be very svelte. Oddly, while OpenCores has a few CORDIC projects, we didn’t see any written in Verilog. We did however find a few on GitHub, including a fairly complex one from [ZipCPU].
The history of CORDIC is interesting, too. [Jack Volder] worked for a defense contractor and had the task to replace the analog resolver on a B-58 bomber’s navigation computer with something both more accurate and real time. He conceived CORDIC in 1956 based on formulae found in the CRC Handbook but left the company before they built devices that used them. In 1965, [Volder] build Athena, a desktop calculator using CORDIC but Hewlett-Packard didn’t bite on it, although it did influence early HP machines.
















The transcendental functions on the Sinclair Scientific Calculator also use CORDIC. That’s how a chip meant for a simple 4 function calculator gained the ability to do trigonometry.
Your comment lead to a ‘name click’, but it’s not fleshed out. Do so… :)
fat finger while composing comment. Pressed post before url was all typed up…
I don’t like being the citation needed guy, but do you have a ref for that? I thought the Sinclair Scientific used much dirtier approximations, some of which were only accurate to a few decimal places.
That’s the beauty of CORDIC it generates one bit of the answer per loop, so it can be both “dirty” or precise depending how many iterations are performed
This is very useful for a lot of things.
I also used it in my own project:
https://hackaday.com/2018/06/11/fpga-persistently-rick-rolls-you/
Once I’ve used CORDIC, too, for this project:
http://www.frank-buss.de/SignalGenerator/index.html
This is the source code:
http://www.frank-buss.de/SignalGenerator/vhdl/cordic.vhd
Unlike the version from Hamster, in my version the individual steps are executed each at one clock cycle. Hamster synthesized all steps in one loop. This could be a problem for high clock rates.
This is the C program to generate the table and to measure the error:
http://www.frank-buss.de/SignalGenerator/software/table/table.c
BTW, for modern FPGAs and CPUs it doesn’t make sense to use CORDIC, because they have hardwired multiplication.
CORDIC can also do division. Isn’t it useful for FPGA even if it has a hardwired multiplication?
If you need sine and cosine in Verilog there is a nice and concise implementation from James Bowman: https://github.com/jamesbowman/sincos It uses Chebyshev polynomial approximation instead of CORDIC.
Seems like the kind of stuff you would use in a special chip to do 3D on a 16-bit game system. Very cool.
I’ve played around with the Verilog in that first Github link. Works great.
Actually, IntelFPGA (Altera) has its own IP-core of CORDIC in Quartus II for different purposes like from 16.0 version