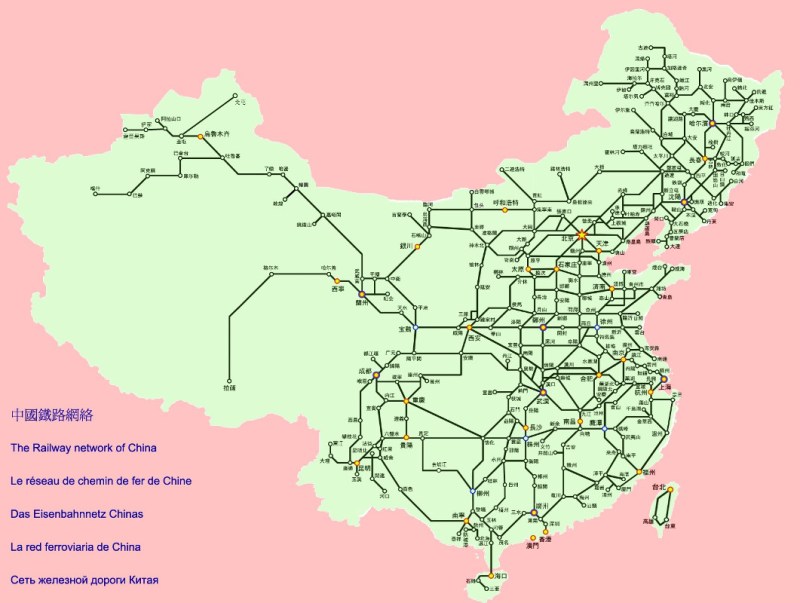
If you’re headed over to mainland China as a tourist, it’s possible to get to most of the country by rail. China is huge though, about the same size as the United States and more than twice the size of the European Union. Traveling that much area isn’t particularly easy. There are over 300 train terminals in China, and finding the quickest route somewhere is not obvious at all. This is an engineering challenge waiting to be solve, and luckily some of the students at Cornell Engineering have taken a stab at efficiently navigating China’s rail system using an FPGA.
The FPGA runs an algorithm for finding the shortest route between two points, called Dijkstra’s algorithm. With so many nodes this can get cumbersome for a computer to calculate, but the parallel processing of a dedicated FPGA speeds up the process significantly. The FPGA also includes something called a “hard processor system“, or HPS. This is not a soft-core, but dedicated computing hardware in the form of an ARM Cortex-A9. Testing showed that utilizing both the HPS and the FPGA can speed up the computation by up to ten times over a microcontroller alone.
This project goes into extreme detail on the methodology and the background of the math and coding involved, and is definitely worth a read if you’re interested in FPGAs or traveling salesman-esque problems. FPGAs aren’t the only dedicated hardware you can use to solve these kinds of problems though, if you have a big enough backpack while you’re traveling around China you could also use a different kind of computer.















“With so many nodes this can get cumbersome for a computer to calculate”… really? shortest path in a 300-node graph? What kind of computer would have trouble with this?
Not so fast,you´re not riding the highway, we deal with trains here.
It´s not really about distance, it´s about time. Matching those timetables and exceptions (like “Not running on Sunday”. “Only on non-working days”) is a much more complex task than the well-known “shortest path in x nodes” !
There’s no direct correlation between distance and duration on streets. Actually trains are much, much easier since you can just look up both the travel and waiting times for huge segments as constants in the timetables, while you have to calculate a good guesstimate for streets. There are no lookup tables for things like “average travel time on the highway between cities x and y on a Monday at 5 PM”, but these tables simply exist for trains.
I used to work on optimisation strategies for truck logistics planning, and I also hold a degree in Railway System Engineering (not a joke). We had long, long algorithms for approximating travel times on streets, and about two thirds of the criteria we used for trucks would be unnecessary for trains.
I’ve once done a routing system for city bus company. Granted, there were only 200 bus terminals, but there were timetables and it provided simple walking directions. It ran fast in php on single cheap server, no fpga or c necessary, and I was still at uni back then. Also my very slow cheap offline gps device can generate best route through half of europe (millions of nodes, 4gb of route data on sd card) in several seconds…
That actually depends on the amount of edges and the weight of each edge. Also, certain considerations must be accounted for depending on the how the entire system is mapped. Lastly, being that this is more or less an embedded controller project (to allow for implementation at each station), the resources of many microcontrollers might be too small to deal with the problem in a fast enough manner. As a side note, this could easily become a mobile app for convenience though and completely eliminate the need for a stand-alone unit.
Student projects aren’t always revolutionary even when novel. Still, if they’ve got a model that does Dijkstras Algorithm in hardware then with a high-end FPGA or ASIC maybe it could find use in high-end routers.
The downside of this is its all theoretical, and does not match actual trains to actual locations. There’s no realtime active tracking.
Good job for a course project, but in real life no one would do it this way….
300×300 = 90k start,destination pairs, this could easily be precalculate and stored in a lookup table.
Assuming a 20 station max route, the naive approach of storing each route in 40byte as a uint16[20] array, would take ~3.4 Mb, using 9 bits of each station in the route, would drop that to ~1.9 mb, at that point just doing a huffman or a lz compression would drop this in the size of ‘high end’ micro-controllers with 256k> flash or just plain flash chips.
Hell even the original 3.4mb table can be put to an sd card…
“300×300 = 90k start,destination pairs, this could easily be precalculate and stored in a lookup table.”
Ha. you never went by train I think. that may be true for time x and one single train per start-destination. This is seldom the case and a change of several trains is most times the case. Now include different timetables, , sunday, weekends, after hours. special trains. just do the math. fortunately whole china has the same time zone…
Here in The Netherlands we have a fine grid of trains for public transport and we use 9292.nl or ns.nl to plan our trips. 9292.nl even has buses or trams included.. try that on a sd card with all the changes due to accidents or other disruptions of the timetable.
couldn’t you do this “analog?” You could wire together a bunch of resistors where each resistor has a higher resistance if it has a higher “distance” then have some LEDs between each. Voltage in goes on your “starting station” voltage to ground goes on your ending station – then just follow the lights?
Funny idea!
Then what? Find the brightest route? Electricity doesn’t only take the path of least resistance, it takes all paths. You might be saved by ramping the voltage up from zero as you overcome the forward voltages of the LEDs.
Exactly (more or less). The “sub optimal” LEDs would be noticeably dimmer.
well, consider I’m currently working with multiple shortest paths calculations on multiple thousand node graphs, it takes short time even for a low power machine. I really don’t see why FPGA should be required for this.
I think the point is to demonstrate that, as with many embarrassingly parallel problems like dijkstra, an FPGA can solve it much faster than a CPU, even a reasonably fast ARM C-A9. It’s not meant to be a practical solution to this particular problem.
One could try DNA?
https://www.nature.com/news/2000/000113/full/news000113-10.html
I don’t think this is a hard issue. The Dijkstra algorithm here is the same one used by the OSPF network routing protocols that have been is use for many many years. No matter how complex that rail network is, it cannot approach the number of nodes and paths in an even moderate sized computer network. Your off the shelf low end network router can run this algorithm very quickly and efficiently.
Here would be the only complex part of the problem. You would have to calculate the best route at any given moment because you have to take into account the timetables. You would have to run the algorithm a lot of times. So for example you would have to calculate the best path from Station A to Station B at each minute of the day because the available trains change so the network looks different. Even doing this though is not a difficult problem because the schedule is known in advance.
The problem here is the horrifying software implementation of Dijkstra’s Algorithm. Unnecessarily O(n^2) when it can be done O(n log n). Better implementation will probably result in a 50x speedup. Add a path heuristic to it (turn it into A*) and it’ll run even faster.