Muon tomography (muography) is the practice of using muons generated by cosmic rays interacting with Earth’s atmosphere (or equivalent) to image structures on Earth’s surface, akin to producing an X-ray. In lieu of spending a lot of spending a fair bit of money on dedicated muon detectors, you can also hack such a device together with two Geiger-Müller tubes and related circuitry for about $100 or whatever you can source the components for.

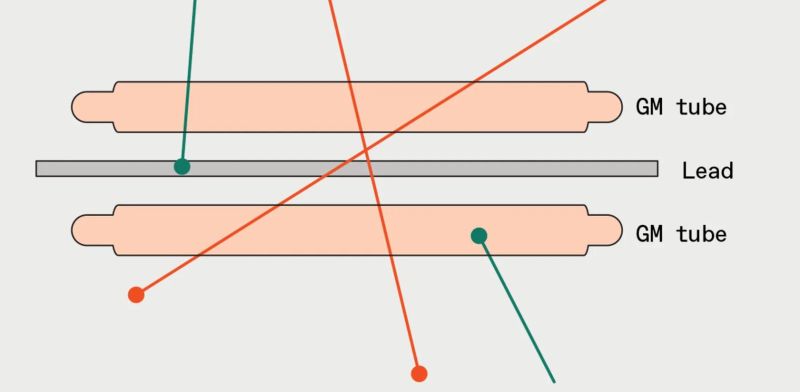
The reason for having two Geiger-Müller tubes is to filter out the countless other (much more prevalent) sources of ionizing radiation that we’re practically bathed in every second. Helped by a sheet of lead between both tubes, only a signal occurring at the same time from both tubes should be a muon. Specially cosmic ray muons, as these have significantly more kinetic energy that allows them to pass through both tubes. As a simple check it’s helpful to know that most of these muons will come from the direction of the sky.

The author of the article tested this cobbled-together detector in an old gold mine. Once there the presence of more rock (and fewer muons) was easily detected, as well as a surge in muons indicating a nearby void (a mine shaft). While not a fast or super-easy way to image structures, it’s hard to beat for the price and the hours of fun you can have while spelunking.