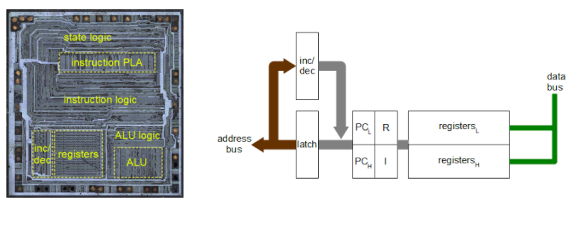
Increment and decrement. They sound like simple functions. But even the simplest functions can get quite complex in a microprocessor design. Ken Shirriff has written up a great blog post about his reverse engineering of the Z80’s 16-bit increment/decrement circuit. The Zilog Z80 was one of the most popular microprocessors of the 70’s and 80’s. It was used in many classic computers such as the Osborne 1. These machines would often use the Z80 to run the popular CP/M operating system.
The increment/decrement circuit is responsible for updating the program counter register during normal (non branch) operations. The increment/decrement circuit also handles the stack pointer register during stack operations, as well as several other functions. One might wonder why a separate adder would be used when the microprocessor has a big ALU available to it. The answer is twofold. First the ALU is already in use handling user math operations. Secondly the increment/decrement circuit has to be fast. A generic ALU just won’t be fast enough.
One classic adding circuit is a Ripple Carry Adder. Ripple Carry Adders get the job done, but they are slow. Note slow is measured in nanoseconds here – there are no clocks involved in the circuit. The whole thing becomes a classic combinational logic optimization problem. Each layer of logic adds a gate delay to the circuit. As the carry has to ripple through all 16 bits, there are 16 gate delays before the final result is available at the outputs. Delays like these are what limits the maximum clock speed for a given circuit.
The Z80 uses some tricks in its increment/decrement circuit. The first is Carry-lookahead. A carry-lookahead circuit will calculate the carry values directly from the inputs. This reduces the gate delays significantly, but it requires more real estate on the die. A second trick is the carry-skip circuit. Carry-skip calculates the result for groups of bits rather than each bit individually. Again, it will reduce gate delays, at the cost of real estate. The actual Z80 implementation uses a mix of both circuits. Several other “helper” circuits are also used. Surprisingly the Z80 has specific logic just to check for 1 (0x0001) on the internal address bus. This circuit is used during memory move loops to inform other parts of the chip that a loop is about to complete.