[Jeff Laughton] was contacted by a customer that was interested in adding some automated functions to a printing press. Before eventually settling on a microcontroller for the job, [Jeff] went old school and started looking at logic gates, counters, and flip-flops. This lead him to the Motorola 14500 industrial control unit, a minimal processor with only 16 instructions. After a few ‘back of the napkin’ sketches, he came up with an extremely minimal computer that doesn’t use a microprocessor. It’s an interesting design notable not only for its electronic brevity, but also because it only uses one instruction.
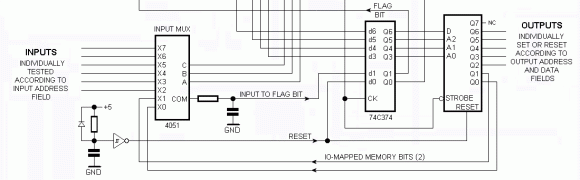
The only instruction this computer will ever execute is an input test, the result of which controls a two-way branch. Instructions consist of an input address, output address, and a single bit of data. If the data bit is true, the computer jumps to one location in ROM, and if the data bit is false, a jump to another location is executed.
A computer really isn’t a computer without some form of memory, and this design is no exception. [Jeff] managed to add two bits of data between the 8-bit latch and 8-bit multiplexer in the design. This is enough to call a few subroutines which test the I/O-mapped memory to decide what the next instruction should be.
It’s a truly bizarre design, but actually much closer to a true Turing machine than the computers in your pocket, on your wrist, on your desk, and in your car.
Thanks [James] for the tip!















A lovely PLC style architecture. I’ve been pondering something similar in an effort to figure out what the fewest discrete logic ICs you can use to make a turing complete machine is; this might just be it.
One neat wrinkle that’s not mentioned is that you can also use the input from the _previous_ comparison directly (after the branch) to decide what instruction to execute. This could enable features such as checking a ‘select’ input in one clock cycle, which then determines which input or output you modify the subsequent cycle.
And two of the 16 instructions are NOPs :)
The MC14500B is the first programmable thing I ever played with. I built a system with a hex keypad, 16 LEDs, 8 switches, all with parts I got as samples from Motorola. I still have a few parts, and the classic red book for it.
I keep thinking about laying out a PCB, but then it’s so easy to do one in VHDL, too.
I remember an ad for an air conditioning company (Honeywell or Carrier) that bragged about their “smart” HVAC, and they had an image of a PCB rotating past. You could clearly read the MC14500B on the chip. This was back in the mid-80’s, IIRC.
But as fun as the ‘500 was, I’ll take my 6502’s and 6800’s any day :)
“but actually much closer to a true Turing machine than the computers in your pocket”
Not quite. It is lacking memory.
“A computer really isn’t a computer without some form of memory, and this design is no exception. [Jeff] managed to add two bits of data between the 8-bit latch and 8-bit multiplexer in the design. This is enough to call a few subroutines which test the I/O-mapped memory to decide what the next instruction should be.”
Fuck, man, you mean you need to read shit?
I know. I can read too. But even taking into account a few bits, it’s still lacking memory to behave like the infinite amount of memory that a Turing machine has. Your regular computer, with a few GB of RAM, comes much closer. So, saying that this device is closer to a Turing machine is incorrect.
It would be better to compare it with a state machine, which isn’t as computationally powerful as a Turing machine.
He does call it a state machine in the circuit diagram file name.
But it is Turing complete. ‘Turing complete’ has noting to do with computational power. Even your desktop PC has a finite number of ‘states’ all be it an exceptionally large number of states.
I am guessing by its function that it is coded to behave as a state machine and anything that can emulate a state machine is likely to be (although not necessarily) Turing complete. This however does not make an actual state machine Turing complete.
I can see the confusion here. With 4 bytes per ‘if goto’ and only 2KBytes of ROM it certainly looks like a state machine on first glance. But state machines do not have a conditional branch. State machines instead have only state transitions.
1) Is this Turing complete – YES
2) Is it a state machine – I suspect it is coded to emulate a state machine but as far as hardware is concerned – NO.
That’s my ‘opinion’ anyway.
PS: I am delighted to see someone doing this at a very ‘nuts and bolts’ level.
A conditional branch can be encoded as a state transition. In fact, any computing device with finite memory can be implemented as a Finite State Machine. You just assign a different state to each bit vector in the memory, so if you have N bits of memory, you’ll get 2^N different states. Any operation of this device (including branches) are nothing more than transitions from one state to another.
For a machine to be Turing complete in the theoretical sense, it needs infinite memory. And as you can read here: http://en.wikipedia.org/wiki/Finite-state_machine “Considered as an abstract model of computation, the finite state machine is weak; it has less computational power than some other models of computation such as the Turing machine.[1] That is, there are tasks which no FSM can do, but some Turing machines can. This is because the FSM has limited memory. The memory is limited by the number of states.”
Obviously, true Turing Complete machines don’t exist, but as long as you only run a subset of programs that only need limited memory, you can pretend they do. Obviously, with just a few bits of memory, the subset is going to be noticeably limited.
Bravo Maestro!
Title is inaccurate (yes I’m a pedant); this is a CPU, albeit a simple one. Next you’ll be telling me that bit-slice machines and old mainframes don’t have CPUs either.
No it is not a CPU it is a finite state machine.
Just because it’s a state machine doesn’t mean it isn’t also a CPU. All CPUs are state machines, but not all state machines are CPUs, they must be turing-complete.
The title seems to have been written with the (false) assumption that all CPUs are microprocessors.
http://en.wikipedia.org/wiki/Central_processing_unit#Transistor_and_integrated_circuit_CPUs
Could be implemented more cheaply and esily with a single attiny chip.
And most importantly, with a attiny (or any other non-esoteric solution) it will actually be repairable, upgradable, and maintainable.
Early on in the article the author states he switched to a microcontroller when additional machines were automated.
looks like a variant of the state machine I designed that nobody was interested in :)
For simple automation a state machine will do the job. For work, I planned replacing an obsolete PLC with a logic based state machine. No worry about obsolescence. Cycle of the machine never changed and it was all on/off inputs and outputs.
I’d actually be interested in reading about your design — care to post a link?
Sorry about being so delightfully nonspecific — my comment immediately above was directed at rue_mohr…
Isn’t a latch a memory?
how is this a computer without a cpu? it IS a cpu all the way. nice website mr laughton has btw cool other (repair) projects.
In other words this is a solid state replacement for a bunch of low voltage control relays.
Big hat tip to Jeff Laughton from somebody who was doing just this sort of industrial service and design work in the 70’s and 80’s (including Rheometers and printing presses). I hope he gets the same personal satisfaction I did from “fixing the unfixable”.
This kind of ROM/latch state machine is pretty uncommon in practice but can be a very effective solution, as Jeff has illustrated. While his application uses a low speed clock one of the features of this approach is that it can provide quite fast and stable timing.
Some years ago Elektor magazine featured a circuit that flipped the copy protection bit in a Digital Audio bitstream using a variation of this technique by bit shifting the stream in looking for the trigger bit pattern and flipping the required bit to the unprotected state on the fly.
I used a hard-wired variation of this technique on a line of packaging machine controllers and far from being difficult to service plant electricians loved it. The actual hardware could be serviced with nothing more than a circuit and multimeter, and in day to day operation it stopped at a faulty state (shown on a simple display) and pointed directly to the limit switch or whatever that required attention.
uP’s are wonderful, but they aren’t the only game in town. A state machine like this can be serviced in an hour with no need to spend a week dumping and hand disassembling undocumented complied object code – http://laughtonelectronics.com/Service/Embedded%20Computer/embedded%20computer.html
I think some of the commenters need to get out on the factory floor a bit more often.
It’s a Moore state machine coupled with a ROM/register that transitions on alternate phases of the clock. The ROM/register is a simple microprogram. A very clever design!
Earlier in my career I worked on a microprogrammed 2901 bit-slice processor and another design which used a PLD, register and SRAM to do something very similar (it looked up the required output port in a Token Ring switch, based on the source routing field in the packet).
I would REALLY love to see a program written for this device… or more information about how to program it.
without a CPU or with a very simple CPU??!!
how come in all my years of reading,
the ONLY place i hear the word “turing” is on this site?
“a turing machine has infinite memory”
what the (heck)?
where can i buy this paradoxical cure-all????!?!?!?!????
is it infinite dollars? is there a payment plan? lol
if it does not exist, why do people keep defending it
like its a favourite chip or something?
its like those people that argue that
an 90’s desktop computer has a conciousness?
no it doesnt, anyone saying this is clearly
uninformed, misinformed, ignorant, or just plain trolling.
how money is made of off books on that is another story…
Retard