Grandma’s Phone, DSL, And The Copper They Share

February 5, 2016 by Rud Merriam 79 Comments

My DSL line downloads at 6 megabits per second. I just ran the test. This is over a pair of copper twisted wires, the same Plain Old Telephone Service (POTS) twisted pair that connected your Grandmother’s phone to the rest of the world. In fact, if you had that phone you could connect and use it today.

I can remember the old 110 bps acoustic coupler modems. Maybe some of you can also. Do you remember upgrading to 300 bps? Wow! Triple the speed. Gradually the speed increased through 1200 to 2400, and then finally, 56.6k. All over the same of wires. Now we feel short changed if were not getting multiple megabits from DSL over that same POTS line. How can we get such speeds over a system that still allows your grandmother’s phone to be connected and dialed? How did the engineers know these increased speeds were possible?

shannon_maze_hr — Claude Shannon with his maze running mechanical mouse

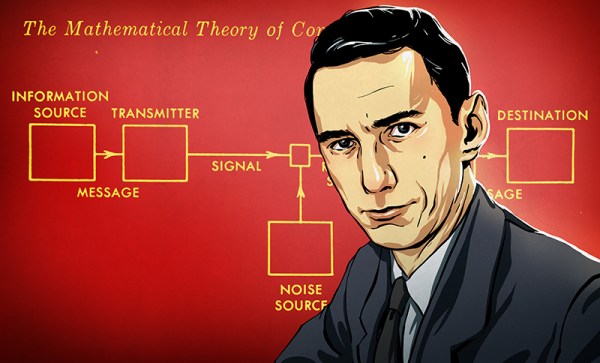
The answer lies back in 1948 with Dr. Claude Shannon who wrote a seminal paper, “A Mathematical Theory of Communication”. In that paper he laid the groundwork for Information Theory. Shannon also is recognized for applying Boolean algebra, developed by George Boole, to electrical circuits. Shannon recognized that switches, at that time, and today’s logic circuits followed the rules of Boolean Algebra. This was his Master’s Thesis written in 1937.

Shannon’s Theory of Communications explains how much information you can send through a communications channel at a specified error rate. In summary, the theory says:

There is a maximum channel capacity, C,
If the rate of transmission, R, is less than C, information can be transferred at a selected small error probability using smart coding techniques,
The coding techniques require intelligent encoding techniques with longer blocks of signal data.

What the theory doesn’t provide is information on the smart coding techniques. The theory says you can do it, but not how.

In this article I’m going to describe this work without getting into the mathematics of the derivations. In another article I’ll discuss some of the smart coding techniques used to approach channel capacity. If you can understand the mathematics, here is the first part of the paper as published in the Bell System Technical Journal in July 1948 and the remainder published later that year. To walk though the system used to fit so much information on a twisted copper pair, keep reading.

Continue reading “Grandma’s Phone, DSL, And The Copper They Share” →

Building The World’s Smallest RGB LED Cube

February 5, 2016 by Brian Benchoff 33 Comments

What’s the smallest RGB LED cube? A 1x1x1 cube is easy, but it’s a stupid joke and we’ve heard it before. No, to build the smallest LED cube, you’ll have to stuff 64 RGB LEDs into a cubic inch, like [Hari] did with his miniscule LED cube.

A single column of Charlieplexed LEDs. Note the resistor for scale.

One might think that individually addressable RGB LEDs are the way to go with an LED cube this small. Anything else would hide the LEDs behind a mess of wires. This isn’t the case with [Hari]’s LED cube – he’s using standard surface mount RGB LEDs for this build. But how is he connecting the things?

The entire build was inspired by the a much earlier project, the Charliecube. This LED cube, like [Hari]’s uses Charlieplexing to condense all the connections for a column of LEDs to only four wires. Repeat that sixteen times, and [Hari] built himself a tiny, one-inch cube of glowey goodness.

The cube itself was built with a PCB backplane designed in Eagle and fabbed at OSHPark. The LEDs are driven by an Arduino Nano. If you’d like to build your own, or you’re a masochist for dead bug soldering, you can grab all the design files over on [Hari]’s hackaday.io project page.

Continue reading “Building The World’s Smallest RGB LED Cube” →

“You Sank My Dysprosium!”: Periodic Table Battleship

February 5, 2016 by Dan Maloney 18 Comments

Kids these days, they have it so easy. Back in the old days, we learned our elements the hard way, by listening to “The Elements” by Tom Lehrer over and over until the vinyl wore out on the LP. Now, thanks to [Karyn], kids can learn the elements by playing “Battleship” – no tongue-twisting lyrics required.

For anyone familiar with the classic “Battleship” game, you’ll wonder why no one thought of this before. [Karyn]’s version of the game is decidedly low-tech, but gets the job done. She printed out four copies of the periodic table, added letters to label the rows, and laminated them. A pair of tables goes into a manila file folder, the tops get clipped together, and dry-erase markers are used to mark out blocks of two to five elements to represent the ships of the Elemental Navy on the lower table. Guesses at the location of the enemy ships can be made by row and series labels for the elementally challenged, or better yet by element name. Hits and misses are marked with Xs and Os on the upper table, and play proceeds until that carrier hiding in the Actinide Archipelago is finally destroyed.

This is pure genius in its simplicity and practicality, but of course there’s room for improvement. The action-packed video after the break reveals some structural problems with the file folders, so that’s an obvious version 2.0 upgrade. And you can easily see how this could be used for other tabular material – Multiplication Table Battleship? Sounds good to us. And if your nippers catch the chemistry bug from this, be sure to take a deeper dive into the structure of the periodic table with them.

Now, if you’ll excuse me: “There’s antimony, arsenic, aluminum, selenium, and hydrogen and oxygen and nitrogen and rhenium….”

Continue reading ““You Sank My Dysprosium!”: Periodic Table Battleship” →