One challenge to building optical computing devices and some quantum computers is finding a source of single photons. There are a lot of different techniques, but many of them aren’t very practical, requiring lots of space and cryogenic cooling. Recently, researchers at the Hebrew University of Jerusalem developed a scalable photon source on a semiconductor die.
Using nanocrystals of semiconductor material, the new technique emits single photons, and in a predictable direction. The nanocrystals combine with circular nanoantennas made of metal and dielectric produced with conventional fabrication technology. The nanoantennas are concentric circles resembling a bullseye and is used to ensure that the photons travel the correct direction with little or no angular deviation.
A single IC could contain many photon sources and they operate at room temperature. We’ve talked about quantum tricks with photons before. Quantum mechanics is another popular topic.















I’ve been thinking of making a single photon source as part of my optics bench project.
The difficulty is detecting that you have single photons, and this generally requires a photomultiplier. That’s not a problem, but PM tubes are expensive on eBay and require a HV power supply. Also not a problem for the determined hacker, but starting to get out of scope for my project.
Once you have a way of detecting individual photons, you can…
Take an LED and calculate the power, which is voltage drop times current. That’s in watts, which is Joules per second. Perhaps 5mW or so.
You can increase the ballast resistor to reduce the power output, so multiply the resistor by 10 and reduce the power by 10. Perhaps 500uW or so.
You can calculate the cone area of the LED and use a pinhole in a piece of foil to divide this down even further. If the cone has an area of 3cm^2 at 1cm, then a 1mm pinhole at that distance gets 1/300 of the photons, at 2cm 1/600 of the photons get through, and so on. Perhaps 1uW or so.
Knowing the frequency of the LED, you can convert that to energy per photon by Planck’s famous equation: E = (h*C)/lambda. (Be sure to get the result in Joules/photon, not eV/photon.)
Knowing the energy of individual photons, and knowing the energy of your LED (power => Joules/second) you can convert to photons per second.
Hold a glass plate over a candle and blacken it somewhat. Measure the light throughput and set it aside. For example, measure a flashlight with- and without-the glass using a light meter. Note the proportion of light that passes through. Perhaps a factor of 1/10 or so.
Make several of these plates.
Knowing the number of photons per second, add plates as needed to divide this down to a reasonable number. For the calculations above, roughly 16 plates of 1/10 filtering would produce about 3 photons per second. More or less.
You can check this with the photomultiplier tube – you should get randomly 3 “clicks” each second.
You can also do clever things like use a polarizer (1/2 the photons get through), or two polarizers at almost 90 degrees apart (cos(angle) photons get through.
I’m told that the glass/lamp black method was how physicists originally generated single photons in the early 1900’s.
The ST VL6180X laser rangefinder has a SPAD on die and is about $6 qty 1. Unfortunately I don’t think there’s a way to get the direct trigger output, only the final distance measurement.
Wow, what a great idea!
I have VL6180X for an unrelated project, so I just scanned through the datasheet. As near as I can tell, the ambient light sensor mins out at about 10^10 photons. All the registers are integrated, so it seems you are correct.
That made me go to eBay, and I discovered you can get boards with integrated regulators (mine are the raw chip), and I can think of several uses for these in the optics bench project.
Thanks for the suggestion – I can add a new set of experiments!
For true cryptographic certainty, you can’t use any of those tricks for single photons. There’s always a small, but non-zero, chance that any photon comes with a buddy right behind it. For truly easedropping-free communications, if you can send everything as single photons, a checksum on the other end will let you know if any of them didn’t make it. Didn’t make it = intercepted = someone’s listening. But if you aren’t certain you’re sending single photons every time, then there can still be someone listening without your knowledge. At least in that application, that’s why single photon sources are important (they call them ‘quantum information bits’ but we were always sold secure comms as the desired application).
A single photon source is straightforward if you have a single emitter. That is, a single point where photons can come out of. Any fluorescent dye at a low concentration will do just fine, though it does take a reasonably powerful objective lens to collect a good number of those photons. You can then detect these with a reasonably sensitive CCD or CMOS camera, which are getting cheaper every day (though still ~$5-10k, prob). You can actually see reasonably bright single emitters with your dark-adapted eye on a microscope, too, if you want.
*Proving* you have a single emitter is the tricky part. You can’t spatially separate the signals if they’re within an Abbe limit of each other and there could be two emitters stuck really close to one another that looks like one diffraction-limited spot. You can observe the bleaching or blinking behavior of the molecules in time. Single emitters should go from full on to full off in a single step without any intermediate steps in between.
The true gold standard is an ‘antibunching’ experiment. This is where you take the arrival times of individual photons on a detector (or really the signal split onto 2 detectors, thanks to detector dead times) timed down to the picosecond level. A correlation of the signal *should* produce a dip at zero delay that goes down to 1/(number of emitters in your focus) and a rise slope corresponding to the lifetime of the emitter’s excited state. These experiments are a royal pain in the ass to (compared to the bleaching/blinking approach) because any uncorrelated background or scattered light is going to kill off your antibunching signal. You’re also trying to collect a bunch (1e5-1e6) photons from a molecule that might only live for a second or two if you’re lucky. Inevitably the instant you find a molecule and get it aligned into the fiber input it bleaches without giving any useful signal.
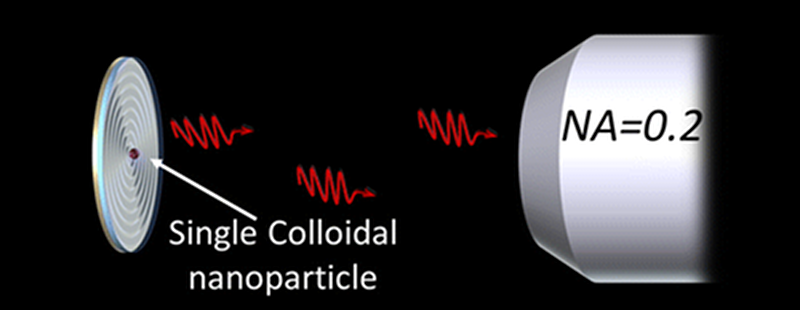
The article above actually makes that job easier by directing more photons into the objective lens. The usual rule of thumb for a high NA microscope is ~5% of the photons from an emitter make it into the objective lens opening. They’re reporting a 20x increase in their low NA system, which is awesome! You can also use things like metal nanoparticles to increase the photon throughput (quantum dots are actually a horrible choice) and total lifetime before bleaching. Would be awesome if you could buy a chip with single embedded emitters (maybe already fiber-coupled) on them one day.
Wow – learned some new optics today. Wikipedia article on “supercritical angle fluorescence microscopy” is pretty thin – know anyone who could improve it? :-)
https://en.wikipedia.org/wiki/Supercritical_angle_fluorescence_microscopy
Excellent comment.
Re bleaching: embedded semiconductor quantum dots are significantly more stable in that regard and the surrounding material lends itself to the implementation of photonic structures. That way you can achieve stronger coupling to the light field.
With the possibility to charge tune the electron / hole population by shifting the dot energy levels w.r.t. reservoirs the type and time of the radiative recombination can be controlled.
There are other downsides, mostly again the need for cryogenic cooling and internal fields and strains that mess up the photon energy… but at least the lifetime is good.
I should say that everything I do is in aqueous solution at RT, but are quantum dots better behaved when embedded? In solution they don’t bleach, but they blink on all timescales (as opposed to organic dyes, which are usually limited to ~microsecond blinking).
Of course, if you cool everything down to 77 K, lots of things change…
There’s often a way to produce core-shell type colloidal QDs which are less prone to oxidative damage. Depending on the extent to which the wavefunction is confined it “sees” trapped charges and defects in the surrounding.
When expectations are lowered a nearly ideal system is the N-V center in nanoscale diamonds (e.g. http://www.sigmaaldrich.com/technical-documents/articles/technology-spotlights/fluorescent-nanodiamond-particles.html )
From what I’ve read so far Ge or N vacancy dots can have excellent second order correlations and preserve some of that up to RT.
I wonder if nm scale Tesla coils that work in the Thz range would be an effective method to generate single photons. Maybe using carbon nanotube forests coated with buckyballs and built on a plate capacitor or metal crystals shaped by cymatics whilst being grown with electrolysis.
Wow. Last time I had a trip that wild was in 1982, on some really good acid.
I don’t need drugs to think like that. [ and that’s tame for me. ]
One day I’ll think of something useful, that can actually be built in my life time, that someone hasn’t already discovered. They’ll probably discover it in my notes, centuries after I’m gone, when someone else has already gotten a Nobel prize for it :D
Maybe it’s easier to create lots and then tap them off.
You can apply for a login to let you play with a quantum computer belonging to IBM, here: https://quantumexperience.ng.bluemix.net/ It is not optical but it does have 5 qbits, and it is the real thing.
I have zero knowledge whatsover on how Quantum computers work, but isnt 5 qubit the same as a standard 32 bit register computer?
Well… it is definitely more powerful than an 8 bit Arduino. :-)
From what I understand, it means you can factorize instantly a number that’s smaller than 32. Great, isn’t it ?
In the tutorial docs they actually point out that you need 50 qbits to out compute any other standard computer in existence. That would be on any problem, not just the ones suited to a quantum computer.
the bitcoin network is already finding 60+ bit hash collisions, but I presume networked computers don’t count…
So when IBM have a 100 qbit machine it basically destroys bitcoin’s value as a currency system, instantly? What about the work at UNSW re scalable qbit systems on silicon? I don’t know if your original comment is a sensible comparison, but if it is that is the conclusion one draws, crypto currencies are doomed.
@ Dan:
When there is any indication of an n-bit quantum computer cryptocurrencies (and classical banks closed source ‘inaccessible’ cryptocurrencies) will have to switch to higher security parameters say 3*n bits. scalable qbit systems have been announced for decennia, it’s the “nuclear fusion” for calculations.. building a low qbit system, demonstrating it works, and then claiming it is scalable is just that… a claim. Perhaps achieving the accuracy of a setup scales exponentially with qbit count, perhaps the coherence time decreases exponentially with qbit count, etc…
Perhaps cryptographic key sizes on quantum computers has already been done and whatever security apparatus is already using it… but even then endusers can simply use postquantum cryptography with large enough keysizes on classical computers…
Unless a truly scalable system is possible and has been constructed… in that case there must be a fundamental relationship between computatoinal speed and memory space. currently exponential acceleration on a classical system can be achieved with enough memory: for accelerating exponentially an n-bit virtual system one needs (2^n)*log((2^n)!) bits on a classical system, but that is a lot!
correction:
for accelerating exponentially an n-bit virtual system one needs log((2^n)!) (which is smaller than (2^n)*log(2^n) ) bits on a classical system, but that is a lot!
also the log’s I took are all base 2
A better way to phrase it would be this:
Denote with P[n] the class of polynomial algorithms on n-bit state machines, and NP[n] the class of non-polynomial algorithms on n-bit state machines. then already today:
P[log_2((2^n)!)] = NP[n]
so if you have a harddrive of 1 Terrabyte HDD, you can calculate the (2^t) state of a 15bit finite state machine in t constant timesteps…
sorry I plugged in the wrong numbers: its 37 bits
so if you have a harddrive of 1 Terrabyte HDD, you can calculate the (2^t) state of a _37_ bit finite state machine in t constant timesteps…
since log_2( (2^n)! ) = (2^n)*log_2(2^n)=n*2^n…
so 37*2^37 is roughly 10^13 or near 8*10^12 bits
https://hackaday.io/project/8137-prime-factor-reduction-sieve Say what now?
There is far more to that project than simply generating single photons.
The “single photon” part is easy: If you stand 3 metres from a 1 milliwatt source (which is still a lot of light: plainly visible) then at any time, on average, there is only a single photon in existence between that light source and your eye pupil.
It’s the ‘on average’ that kills it. For lots of applications you have to be certain that you have a hard upper limit of 1 photon at any time. Single emitters do this, but coupling yields are crap (5% at most, and even that’s hard). This seems to get 20% on a much cheaper and easier system.
Yes, getting a single photon is easy. Creating ONLY one photon when you want is the hard part.