A few years ago, there was a stir about a new fundamental component called a memristor. That wasn’t the first time a new component type was theorized though. In 1948 [Bernard Tellegen] postulated the gyrator. While you can’t buy one as a component, you can build one using other components. In fact, they are very necessary for some types of design. Put simply, a gyrator is a two-terminal device that inverts the current-voltage characteristic of an electrical component. Therefore, you can use a gyrator to convert a capacitor into an inductor or vice versa.
Keep in mind, the conversion is simply the electrical properties. Normally, current leads voltage in a capacitor and lags it in an inductor, and that’s what a gyrator changes. If you use a gyrator and a capacitor to make a virtual inductor, that inductor won’t magnetically couple to another inductor, real or simulated. There’s no magnetic field to do so. You also don’t get big voltage spikes caused by back EMF, which depending on your application could be a plus or a minus. But if you need an ungainly inductor in a circuit for its phase response, a gyrator may be just the ticket.
Magic
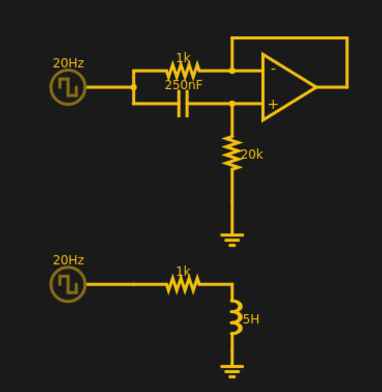So how does a gyrator do its magic? Consider this circuit simulation. The bottom circuit shows the voltage and current in a 5 H inductor. The top circuit shows a gyrator-equivalent circuit providing a similar inductance.
At DC, the bottom circuit will look like a 1 kΩ resistor along with whatever resistance the inductor’s wire presents (probably not much). At some very high frequency, the inductor’s effective resistance will be so high, the circuit might as well be an open circuit. In between, the resistance will increase with frequency.
Before you look at the top circuit, it might be a good idea to review a few analysis tricks for a “perfect” op amp. We can imagine the inputs of the op amp are open circuits. Whatever voltage is on one terminal, the output will do anything it can to make voltage on the other terminal the same. In practice, that isn’t always possible but for our case here, assume it is.
Now consider the gyrator circuit. At DC, the capacitor will be fully charged and be an open circuit. Since the positive terminal of the op amp theoretically draws no current, that terminal will be at ground potential through the 20 kΩ resistor. That means the op amp output is also at 0 V so the 1 kΩ resistor is between the source and ground, just like in the inductor circuit. At a very high frequency, the capacitor will simply vanish and the input voltage will appear the positive terminal. That means the 1 kΩ resistor will have the same voltage on each side of itself and is effectively out of the circuit.
Now let’s think about the phase shift. When the capacitor sees an AC signal, its current will rise before the voltage across it rises. So at the very instant that starts, the resistor will have the same voltage across it and thus no current. As the voltage across the capacitor increases, the voltage at the positive and output terminals will decrease, causing more current to flow. That’s the opposite of the capacitor’s current-voltage response, and exactly like the inductor’s. So even with no real math, you can get a feel for why this works.
Why?
All components we use are not ideal. We pretend wire has no resistance and no limit on current-handling when we draw schematics, but in reality, it has both. Capacitors leak. Resistors can be non-linear or drift. But inductors are especially troublesome. The wire that forms them has resistance. The loops capacitance with the adjacent loops. In addition, inductors tend to be physically large. Big inductors use so much wire that they are not only large but have lots of resistance and other problems. They take up a lot of space. Perhaps not as large as this one from a 1912 radio antenna, but still.
You can usually get high-quality capacitors and you can use them to make large value inductors that are closer to the ideal than a wire-based counterpart. So assuming a gyrated inductor meets your needs, you can usually get a higher-quality device and often in less space by using a gyrator.
One place this is especially important is inside integrated circuits. Due to the way ICs are made it is reasonably easy to make capacitors of particular values, but inductors are very difficult to make in silicon. It is even easier to make multiple capacitors with very precise ratios of capacitance and that can sometimes lead to interesting designs where the exact values of the capacitors and simulated inductors aren’t as important as the ratio between the values.
Since the inductors made with gyrators aren’t actually magnetic, you can’t use them to drive a relay, or a speaker, or sense magnetic fields, or build transformers. You can’t use them in switching power supplies, either. However, you do see them used often in things like filters. Just remember, the op amp (or other active devices) will have to operate at the frequencies involved and still have good properties.
Design
You might wonder why the 250 nF capacitor in the example circuit is the same as a 5 H inductor. After all, the simulation uses a 20 Hz signal which means the inductor has a reactance of about 628 Ω, while the capacitor has a reactance of almost 32 kΩ.
Consider that the 1 kΩ resistor is R1 and the 20 kΩ resistor is R2. Without getting into the derived math, the effective Z of the circuit is:
For the example, that comes out to 628 Ω of capacitive reactance. (If you’d like a refresher on complex impedance, we’ve got you covered.)
The reactance of an inductor with series resistance R1 is 
Just remember, the op amp has to function at the frequency of interest and has to be able to output enough current which will limit how low R1 can be.
Odds and Ends
A gyrator is actually a special use of a NIC or negative impedance converter. You can use the same idea to create negative resistance or even negative reactance. You sometimes see negative resistance used in simple oscillators. Of course, that’s often in the form of a device like a tunnel or Esaki diode that actually has negative resistance, but you could use a NIC circuit, as well.
I’m showing gyrators with op amps because that’s the easiest way to understand their operation. However, you can use other active devices. In addition, the gyrators I’ve shown all require one end to be grounded. There are architectures for gyrators that produce a floating virtual inductance, but those are rare because they take more components.
You can, of course, flip an inductor to a virtual capacitor with the same set up. The problem is there is little incentive to do so. Capacitors are generally smaller, lighter, and–for the same price or lower–better quality than inductors.
Learn More
If you search YouTube for gyrator, you might find some not-entirely-safe-for-work content. Who knew? However, you are safe with [Jeffrey Walling’s] lectures on the topic, which appear below. If you want to dig into the math, you could do worse than these videos.
If you prefer reading, or you are interested in how this was done with devices like vacuum tubes and discrete transistors, have a look at [James Kulesz’s] Master’s thesis. Sure, it is from 1969, but the math hasn’t changed and the only real difference from today is that op amps are a lot better these days.
These large coils were used to cancel out antenna’s capacitance (making a resonant circuit at antenna’s operating frequency). A monopole antenna (such as mast) lower than ~1/4 wavelength will have large capacitive reactance, also short top-loaded antennas have it. With powers used at longwave/mediumwave/low shortwave transmitters (hundreds of kW) , where such antennas are used, a gyrator circuit probably won’t help.
A gyrator isn’t useful when ENERGY efficiency is important — while a gyrator makes the current and voltage appear like another component, the energy stored (1/2C.V^2, 1/2L.I^2 etc.) (and recovered) is not emulated. For antennas, the intent of tuning is ultimately to improve power efficiency, and so a gyrator circuit won’t help there.
I’m pretty sure that is not true. If the electrical specification (relationship between current and voltage) is the same, the energy flows will be the same.
The difference of course is that the energy is stored into, and then extracted from, the power supply. If you want to build a 5H inductor using a gyrator and stuff a couple hundred amps into it, you need an op-amp and power supply that is capable of that power level.
And sure, you can emulate a 5H inductor and it will work well at 20Hz… but the bandwidth of your opamp will limit the bandwidth of operation. You ain’t going to make a gyrator-inductor and use it in an RF filter at 100MHz – it won’t work because you’ll run out of gain-bandwidth product on the opamp.
You can’t make a boost converter from a gyrated capacitor, or a charge pump from a gyrated inductor.
Gyrators approximate the I-V relationships of inductors and capacitors for continuous signals, but the approximation breaks down if you apply discontinuities, like the switching in a boost converter or charge pump. You also don’t get any of the physical behavior deliberately ignored by the lumped-element model of electronics: you can’t make a transformer by putting two gyrated capacitors side by side, or a capacitive touch sensor from a gyrated inductor.
Gyration is a useful technique, but discussing it in terms of passive components is only true for appropriate values of ‘true’. It dives into physical absurdity when you gyrate a resistor to get a negative resistance.
it’s true. In a real inductor, you recover the (1/2.l/I²) energy stored in it when you reduce the current. In an emulated inductor, you don’t — generally (additional) energy is consumed from the power supply and associated op-amp-type circuits that emulate the inductor.
Yum, Master’s thesis. Now just imagine how much ferrous material it would take to shrink that coil down.
Monopole antennas don’t exist. Period.
True, the other ‘pole’ is referenced to ground.
Image source?
You mean of the coil or the original art? The original art is from an IRE proceedings from 1914: https://en.wikipedia.org/wiki/File:Large_antenna_loading_coil.jpg — now fallen into public domain.
Cool. I’ll put that on the shelf next to my Wobulator.
Have to keep it away from the coherer though.
Like the “rumbatron”…
gyrators have been used in active filter circuits for ages. Nothing new here. They are often used to synthesize inductors.
I read most of this article, now my brane hertz.
I remember the early seventies, suddenly lots of talk about gyrators. IC op-amps then making them practical. Various speculation about radio receivers without inductors, nobody giving thought to the need for wide bandwidth op-amps.
About the only place I saw them was in adjustable equalizers, just replacing the very low frequency (and thus high value) inductors with gyrators. Active filters were a different thing, no inductors needed in the first place to replace.
So I can’t think of many audio filters in hobby circles that moved to gyrators. Active filters took over. So all kinds of amateur radio gadgetry like narrow audio filters or radioteletype decoders that had previously used those ubiquitous 88mH toroid coils surplus from the telephone company moved to active filters rather than synthesizing large value coils.
And nobody in hobby circuits went back to really low IFs in superhet receivers to try gyrators in the tuned circuits.
Michael
Very nice article HaD. I say that because in today’s Maker / STE[/A]M Culture, the mathematics of electrical engineering is largely IGNORED. I like that you embedded a link to the HaD post “a refresher on complex impedance”. However in the article complex impedance HaD article it should be said that the X+/-Yj notation is “not correct” IMO (yes I’m from the U.S.) – in EE terms it should be X+/-jY, like in your current post. Also the “a refresher on complex impedance” post should clarify that in EE a complex variable is denoted with a “j”, while in pure mathematics and non-engineering practices a complex variable is denoted with an “i”. (Geez, that may start a Flame War – Sorry). Anyway, Thank you HaD…
Well since j is just Sqrt(-1) I have never been a stickler for X+jY vs X=Yj. In other words, j isn’t a suffix (like MHz), it is just a number multiplied. As for the j vs i, that is in the other post pretty clearly, I think. Didn’t mention it in this post, though.
I prefer to keep the j before the reactance as it signifies that what you are looking at is a complex impedance and not some other algebraic equation or even simple complex number.
I agree, this article had just the right mix of practical intuition and actual math. Good job!
You are largely right. More focus on coding than math itself, thought they are not necessarily separate. Back in the 90’s a coworker of mine got really interested in DSP, which back then meant learning FFTs.
Yeah but that stuff’s REALLY complicated. And for many many things you can do with electronics, particularly digital, you don’t need it. Especially in STEM, where you’re talking about educating people. Bringing in extremely complicated maths isn’t going to inspire people to pick up a soldering iron, but there’s so much you can do without the maths.
It’s a good idea to keep the mathematics out of it. Most people aren’t cut out for it, and certainly don’t enjoy doing it. But if I started off slow, and eventually became interested in doing clever things with radio, say, I might eventually teach myself (or better, get someone to teach me) the maths. If I didn’t care about radio, and just used off-the-shelf modules, I’d be fine as I am.
I realise that it’s not just radio that uses advanced maths like that, but it’s a popular use.
Tempest Storm is my favourite old time gyrator.
Good wobulators there too.
There is a nice example if a gyrator based VLF receiver for sudden ionospheric disturbance (SID) detection over at the AAVSO website
https://www.aavso.org/gyrator-iii-vlf-receiver
It uses a capacitor and a gyrator to form a compact high Q tank circuit between the antenna and the detector.
They are tuned to VLF transmissions from submarine command and control stations that broadcast in the vicinity of 20kHz in the RF spectrum.
Hmm, I really should go and populate the receiver boards I had made and wind the receive antenna…
FAR Circuits makes a bare board. I have one in my collection of projects I would like to build someday before i die.
Excellent article, thank you! As a student majoring in microelectronics engineering, i especially appreciated the remarks about it’s usefulness in ic’s. I wouldnt have minded a little more math. ;). But i can always go learn more on my own. Plus it gives me one more thing to pick my proff’s brains about!
Btw, benchoff would’ve written it better ;). Queue the troll stampede!
typo in “The reactance of an inductor with series resistance R1 is Z = R1+j(2*pi*f*R1) …” should be Z = R1+j(2*pi*f*L)
If gyrators are the fifth element…
…do you use them for building a Mooltipass?
B-)
Our guy hasn’t quite captured Milla Jovovich there. Whether that’s deliberate so she doesn’t sue you, I don’t know.
That said, setting the scene in the Egyptian temple got it completely right! The fifth, previously unknown, stone.