There’s an old saying: Tell me and I forget, teach me and I may remember, involve me and I learn. I’m guilty of this in a big way — I was never much on classroom learning. But if I build something or write some code, I’m more likely to understand how it works and why.
Circuit simulation and software workbooks like Matlab and Jupyter are great for being able to build things without a lot of overhead. But these all have some learning curve and often use clever tricks, abstractions, or library calls to obscure what’s really happening. Sometimes it is easier to build something in a spreadsheet. In fact, I often do little circuit design spreadsheets or even digital design because it forces me to create a mathematical model which, in turn, helps me understand what’s really going on.
In this article I’m going to use Google Sheets — although you could do the same tricks in just about any spreadsheet — to generate some data and apply a finite impulse response (FIR) filter to it. Of course, if you had a spreadsheet of data from an instrument, this same technique would work, too.
This is the first of a series about developing intuition and understanding of signal processing using — mostly — spreadsheets. You probably won’t get a lot of practical use out of this — although if you were logging data from a sensor into a spreadsheet and wanted to filter the readings, this might be your go-to technique. By necessity, we need to learn a bit about generating signals mathematically, but since that’s fairly easy, I’m going to put off the details for a future installment. However, for just about any signal processing job we want to do we’ll need filters. There are several kinds of filters we can have and this post is about the FIR filter.
About FIR
FIR stands for finite impulse response and it is a type of digital filter that might seem like magic. There are plenty of ways to explain it, but here’s the thing: making one is dead simple. The idea is to take a bunch of weights, multiply your data by the weights, and then sum it up. The weights are known as taps and they are just numbers. The more taps you have, the better filter you can make.
As a stupid example, suppose you had data and you had 3 taps of values: 1.1, -0.035, 0.336. These values are stored in an array called TAPS and are used along with another array called DATA. To run the calculation you skip over the first two time points (this calculation must have three data points) and start calculating with the third value:
FILTERED[2]=DATA[2]*TAPS[0]+DATA[1]*TAPS[1]+DATA[0]*TAPS[2]
 That’s it. Instant filter. There are two things, though. One is, a real filter is going to have a lot more taps. That’s easy enough. The other thing is where do we get the value of the taps?
That’s it. Instant filter. There are two things, though. One is, a real filter is going to have a lot more taps. That’s easy enough. The other thing is where do we get the value of the taps?
Turns out that’s an article all by itself. However, there’s a simple practical answer: ask the computer to solve it for us. There are plenty of programs that can compute taps and at least one neat web site called t-filter.
The Easy Way to Compute Taps
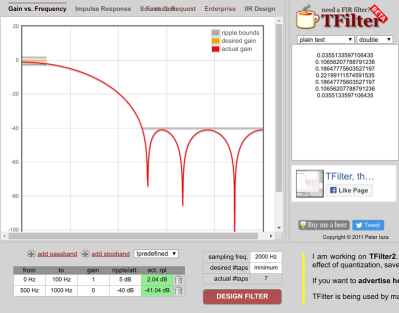
Let’s work out a silly example by hand. Open the t-filter web site and move to the bottom of the screen. The first thing to pick is the sampling frequency. Enter 2000 here. I’m going to keep the sampling rate low to make our spreadsheets more manageable.
You can add passbands or stopbands to the table at the bottom left, but instead, just pick “Low Pass” from the “predefined” dropdown. The page might ask your permission to continue. You’ll wind up with a stock low pass filter that has unity gain at up to 400 Hz and allows 5dB of ripple. There’s also a stopband of 500 Hz to 1000 Hz. Since the sample rate is 2 kHz, it doesn’t make sense to go past half of that. The “desired #taps” box should already say “minimum” and that’s almost always what you want unless you are trying to hit a lesser number of taps.
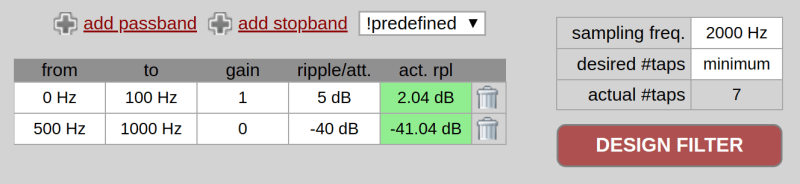
Change the 400 Hz “to” frequency to 100 Hz and press the big red button marked “DESIGN FILTER.” You’ll see seven numbers to the right along with a graph of the filter response. At the bottom, you’ll see that it took 7 taps and the actual ripple figures achieved.
Note the area between 100 Hz and 500 Hz is the “transition band.” The filter doesn’t have to meet any goals in that area. The narrower that transition band is, the more taps you are going to need, in general. For example, if you set a passband of 0 to 100 Hz and a stopband from 110 Hz to 1000 Hz, you’ll get 203 taps (and a long run time, too).
In addition to the taps, you can look at some example code for the filter implementation and the impulse response by using the tabs near the top.
Back to Your Regularly Scheduled Spreadsheet
If you click the “Source Code” tab on t-filter you get C code but that’s not what we are looking for this time. However, we can easily map the calculations in a spreadsheet. I cooked up a spreadsheet on Google Sheets. The sample rate is over in cell J1. The first three rows let you set up to three sine waves that will mix together. You can set the frequency in column B, the amplitude in column F and the phase in column H. If you don’t want a particular frequency you can set its amplitude to zero.
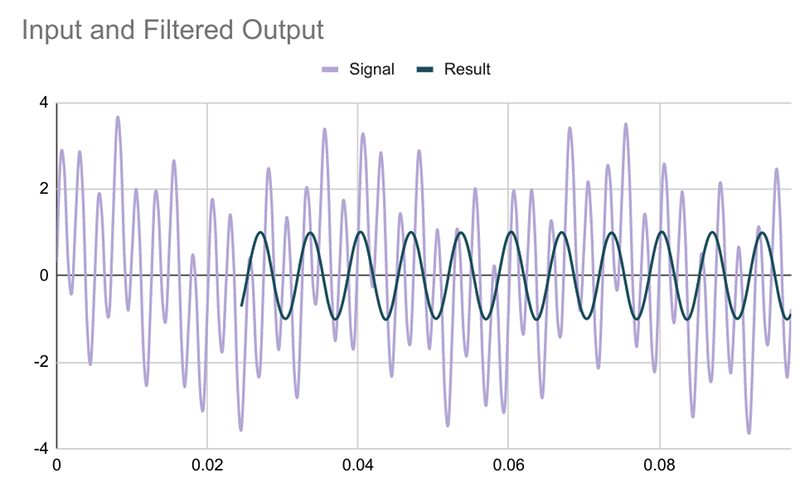
In the spreadsheet, you’ll find two graphs (you might need to scroll right if you’re on a small monitor). The first chart shows the three signals — at least the first bits of them.
The second graph shows the sum of the three signals and the filtered output from column G. That data computes from the signal in column E and the taps in column F. You can copy and paste right from the t-filter site to column F. Using the INDIRECT function, the sheet is smart enough to compute the right value no matter how many taps you have. Here’s how that works (this is a random row from column G):
=IF(ROW()<$J$3,"",SUMPRODUCT(INDIRECT($K$3),INDIRECT("E" & ((ROW()+1)-$J$2 & ":E" & ROW()))))
The cell $J$3 is the first row that can have a valid output, so if we are earlier than that, the answer is nothing. This lets us get enough history to do the entire computation with all the taps.
However, if this cell is a live one, we get the indirect reference in $K$3. This is a reference to the filter taps and changes dynamically depending on what you paste in. The formula for K3 is simple: ="F5:F" & (J2+4)
J2 is the tap count (using the COUNT function) and the four is just a fixed offset since F5 is the first tap. There are no dollar signs on J2 here because I assume you won’t duplicate this formula, although they wouldn’t hurt. In the earlier formula, though, we don’t want the spreadsheet to adjust J2 relative to the new locations, so the dollar signs are needed there.
The same indirect trick computes the range in column E for the signal input. It starts at the oldest sample and runs to the current one, again using the length in J2. Once you have the two ranges set (the taps and the raw data) a simple call to SUMPRODUCT does all the math. That’s it. It really is that easy. The only hard part was accommodating the varying number of taps.
I added a few tabs that have taps for different filters: high pass, low pass, and bandpass. With the default signals (400 Hz, 150 Hz, and 30 Hz) you should be able to filter each one out successfully.
Catching a Wave
The wave generation part of the spreadsheet relies on the well-known formula: y=A(t)*Sin(ωt+Φ) that will be the topic of the next post.
In this formula, y is the output, t is the time, A(t) is the amplitude at time t (a constant, in our case), ω is the frequency in radians/second (the frequency in Hz times 2*π), and Φ is the phase in radians.
If you ever wanted to see what aliasing does when you try to output a signal higher than twice the sampling rate, here’s your chance. Try entering 2000 Hz in cell B1 and then change the phase to a few different values.
You would think you could export the spreadsheet to Excel, and you can — sort of. The graphs are a bit uglier, but even worse, the INDIRECT function chokes on column G in Excel 2007 and Excel Online. After a half hour, I figured out that sometimes (but only sometimes) using ROW() inside the INDIRECT call was causing a problem, but I finally gave up.
By the way, if you are more interested in why this kind of digital filtering works, you could do worse than to read this very intuitive paper from [Lavry Engineering]. If you prefer your filtering old school, check out our Don’t Fear the Filter features, along with [Bil’s] take on a universal analog filter.
Next spreadsheet up? Inside signal generation. Stay tuned.

















Thanks, will review, takes me back to oldie electronic engineering times late 1970’s with great fortune from Clive Maynard to get early exposure to cybernetics and early Ai programming experience of Lisp & Prolog. Good to see an article on FIR here as area of many diverse options seemingly simpler than Ai though offering illusion it has core relevance as if Ai ;-)
FWIW: The processing in our chemical organic biochemical neural nets which bestow seemingly common sense of self and thus basis for our sporadic consciousness (when it’s not on auto pilot) appears rather well a model of equivalent computing as an IIR (Infinite Response Filter) with many more layers in parallel as well as sequential with each summed in regions exploiting a form of an IIR which ends up being as if an FIR with adjustable ‘relaxation time’ comparable to gross neuro transmitters ie memory fallibility in most humans…
Therefore with such a model in mind could well be a straightforward software development path to develop a form of Ai in digital circuitry which might well develop its own sense of self and potentially be suitanly impressed with its own hubris might thus claim it has a soul, let’s hope another form of religion does not consequently emerge, well unless it deigns us as it’s creator and acts with respect we might not always deserve ;-)
Trying to model a brain as a filter for external information is missing half the picture.
Measurements of brain tissue, and corresponding computer simulations, show that our neural networks operate more like chaotic cellular automata – those are a category of systems kinda like Conway’s Game of Life – where the rules are adjustable in a way that the network behaves chaotically for a period and then falls back to being predictable. It has been shown that cellular automata with rules that straddle the point of making the network chaotic maximize the information processing capacity of the network. This effect is known as the “Edge of chaos”.
There’s this narrow transition band from dull and robotic, predictable behavior, and the whole network just dissolving into chaotic noise, and real brains seem to go in and out through this band all the time as if they’re deliberately scrambling themselves to generate new information, rather than merely filtering extraneous information through some rules of logic or mathematical transfer functions that could be described as filters. Moreover, the activation patterns correspond better with non-deterministic chaotic action than deterministic chaotic action that results merely from the rules and arrangement of the network itself.
Deterministic chaotic action is like a double pendulum – predictable in principle but not in practice. Non-deterministic chaotic action is like the double pendulum changing its mass randomly, making it non-predictable both in principle and in practice. All this is suggesting that the brain is leveraging the background noise of itself to generate new information, and that to me seems to be the “ghost in the machine” that is us.
Attempts to model these processes with simulations of artificial neural networks don’t work, because computers can’t do non-determinism. They can go through the motions of generating pseudo-random numbers with an algorithm, but it is a fundamentally different system, or as how John Searle would put it, the computer lacks the necessary “causal power” to implement a mind.
Generating a large number of random numbers by an algorithm – even if the algorithm is originally seeded by a true random event – is not the same thing as having a network that consists of 100 trillion true random number generators itself. The generated numbers are still causally linked, which means there’s just some things the virtual brain cannot do.
To elaborate: suppose the pseudo-random number generator used by the simulation is seeded by the decay of a radioactive isotope to emulate the effect of true randomness, and the computer generates “random” numbers from this seed for all the trillions of neurons that it is simulating.
In this model, the simulated brain is always causally connected through the random number generator. If you know what the seed was, and you know how many program cycles have elapsed since the seed was last changed, you know the state of every single neuron in the system and you can predict how they will respond to any input – in principle.
What the random number generator does is just alter the program every time the seed number is updated, but that does not change the fact that it’s still effectively a completely deterministic program that in itself cannot come up with any new information, new ideas or thoughts. In other words, this is not an intelligent mind any more than a player piano is intelligent, even if you keep changing the music rolls very rapidly.
Just a quick note to anyone who may think the formula for calculating the filtered value with one set of indices going “backwards” is familiar – yup, that’s a 1D discrete convolution. And the taps are nothing else but values of a convolution kernel …
Maybe useful to someone.
1D? Pretty sure you have both amplitude and time/sample index.
It’s 1D convolution because there is only one independent variable (time). 2D convolution usually is used in image processing where the two space dimensions (length, width) are the independent variables.
https://en.wikipedia.org/wiki/Convolution
https://www.dspguide.com is a quite nice book to read about both FIR and IIR and yes everything is basically convolution. Just sometimes its faster to convert it to something else like FFT and then convert back.
Nice to see little or low cost tools for us hackers/hobbyists. Another nice DSP filtering application is OneOverT Digital filter Designer from Tyder.
Al Williams said: “Turns out that’s an article all by itself.” The word “article” in that sentence is a link to here:
https://www.wikiwand.com/en/Finite_impulse_response
Wikiwand is a proprietary commercial front end for Wikipedia that makes money by tracking what you read and then serving you ads through the likes of outbrain.com. Wikiwand also collects user information and sells it to third parties who may or may not comply with Wikiwand’s (lousy IMO) Privacy Policy.
HaD, why are you linking to Wikipedia’s content through Wikiwand? Are you being paid by Wikiwand? I think Wikiwand is a creepy (at best) entity that spies on us for money while stealing the good work of the benevolent Wikipedia and all of us that contribute to it. Please stop linking to Wikipedia through Wikiwand.
Thank You
Hello, thanks for bringing this up. I noticed this site when editing and thought it was a standalone Wiki. Now that you’ve pointed out it’s acting as a frontend, I updated the link to point to the Wikipedia page directly. Thanks!
Just to be clear, that was a link put in by me and I simply forgot to clean it up. I actually use it, but I normally don’t put out links from it because I know it isn’t everyone’s cup of tea.
Back when I was trying to understand DSP, I used Excel to design a low pass filter.
The upper frequency limit equated to a period of about 16 samples, so I had an input pulse 16 samples long.
Then I compared the output to a sine wave (at the cutoff frequency) and adjusted each tap to get as close a match as possible.
I’m sure there are better ways, but this worked for me while keeping the amount of math reasonably low.
Definitely coming back to this one. Doing Advanced Signal Processing in 2nd semester and have not touched DSP theory for at least a year. Also, I have some data from accelerometers in Excel that needs some filtering, so this will definitely help me out a lot.
Thanks Al
To anyone wishing to join/stay with the dark side (Microsoft Excel), the first thing to realise is that copying and pasting from Google Calc to Excel may not copy the formulae. After copying and pasting formulae individually, the main formula in cell G5 downwards
=IF(ROW()<$J$3,"",SUMPRODUCT(INDIRECT($K$3),INDIRECT("E" & ((ROW()+1)-$J$2 & ":E" & ROW()))))
produces an error in Excel, as the INDIRECT syntax differs. In Excel, rather than trying to develop complex logic in the one cell, I found the most straight forward fix was to replace the formula with in G5 downwards with
=IF(ROW()<$J$3,"",SUMPRODUCT(INDIRECT($K$3),INDIRECT(H5)))
and create a new intermediate formula from cell H5 downwards:
="E" & ((ROW()+1)-$J$2 & ":E" & ROW())
I didn’t see your reply until after I already got it working in excel, but I did it a little differently, in that I was working with data from a real sample set. I ended up “hardcoding” some of the INDIRECT references, and also within the SUMPRODUCT equation, I replaced the comma separating the two ranges with an asterisk, which gave me the proper result.
My final formula is:
=IF(ROW()<9,””,SUMPRODUCT($Q$2:$Q$8*INDIRECT(“D” & ((ROW()+1)-7 & “:D” & ROW()))))
The number of taps and the range of the taps is hardcoded.
But overall the filtering worked really well, the t-filter website was a great find for me.