Learning Digital Signal Processing (DSP) techniques traditionally involves working through a good bit of mathematics and signal theory. To promote a hands-on approach, [Clyne] developed the DSP PAW (Portable All-in-one Workstation). DSP PAW hardware and software provide a complete learning environment for any computer where DSP algorithms can be entered as C++ code through an Arduino-like IDE.
Continue reading “Hackaday Prize 2023: Learn DSP With The Portable All-in-One Workstation”
When fully-3D video games started arriving in the early 90s, some companies were more prepared for the change than others. Indeed, it would take nearly a decade of experimentation before 3D virtual spaces felt natural. Even then, Konami seems to have shot themselves in the foot at the beginning of this era with their first foray into 3D arcade games. [Mog] shows us the ins-and-outs of these platforms while trying to bring them back to life via MAME.
These arcade machines were among the first available with fully-3D environments, but compared to offerings from other companies are curiously underpowered, even for the time. They include only a single digital signal processor which is tasked with calculating all of the scene geometry while competing machines would use multiple DSP chips to do the same job. As a result the resolution and frame rate are very low. Nonetheless, [Mog] set out to get it working in MAME.
To accomplish this task, [Mog] turned to a set of development tools provided to developers for Konami in the early 90s which would emulate the system on the PCs of the time. It surprisingly still worked on Windows 10 with minor tweaking, and with some other tools provided over the decades of others working on MAME these old Konami machines have some new life with this emulator support.
Not everything works perfectly, but [Mog] reports that most of the bugs and other issues were recently worked out or are being actively worked on by other experts in the field. If you remember these games from the arcade era of the 80s and early 90s, it might be time to grab an old CRT and fire this one up again.
Continue reading “Reverse-Engineering Forgotten Konami Arcade Hardware”
The Raspberry Pi, although first intended as an inexpensive single-board computer for use in education, is now ubiquitous in electronics communities. Its low price as well as Linux platform and accessible GPIO make it useful in many places outside the classroom. But, if you want to abandon the ease-of-use in favor of an even lower price, the Raspberry Pi foundation makes that possible as well with the RP2040 chip, commonly found on the Pico. [Jason] shows us one way to make use of this powerful chip by putting one in an audio digital signal processing board.
While development boards are available for this chip, [Jason] has opted instead for a custom PCB which he designed himself and includes an integrated headphone amplifier and 3.5 mm audio jacks. To do the actual DSP work, the RP2040 chip uses three 12-bit ADC channels and 16 controllable PWM channels. The platform is also equipped with the TLV320AIC3254 codec from Texas Instruments. With all of this put together, he has a functioning open-source platform he calls the DS-Pi.
[Jason] has built this as a platform for guitar effects and as a customizable guitar amp modeler, but with a platform that is Arduino-compatible and fairly easy to program it could be put to use for anything involving other types of music or audio processing, like this specialized MIDI-compatible guitar effects platform which is built around the same processor.
Much discussion goes on in the guitar world about the best hardware to use. Whether its pickups, how they’re positioned, or even the specific breed of wood on the fretboard, it’s all up for debate. [Eli Hughes] put much of that to one side, however, with his innovative “Active Pickguard” project.
The project reimagines the electronics of an electric guitar from the ground up. Instead of typical electromagnetic pickups, six individual piezo pickups are built into the bridge – one for each individual string. The outputs of these pickups is conditioned and then read by the analog-to-digital converter of a Freescale Kinetis K40. The DSP-capable chip can then be used to apply all manner of effects. [Eli] demonstrates the guitar providing an uncanny imitation of an acoustic guitar, before demonstrating jazz and overdrive tones as well.
The Kinetis chip also features touch-sensitive inputs, which [Eli] put to good use. All the hardware is built into a pickguard-shaped PCB, complete with touch controls for things like volume, tone, and choosing different DSP patches.
Unlike a regular guitar, this one needs a power supply, which it gets via a CAT 6 cable, in place of the usual 1/4″ guitar cable. The CAT 6 also carries audio out to a converter box which allows the audio to be output to a regular guitar amplifier.
It’s a neat build, and one that shows just how modern technology can reimagine a simple 20th-century instrument. DSP really is magic, after all. Video after the break.
Continue reading “Active Pickguard Makes For A Great Guitar Mod”
Like most of us, [Peter] had a bit of extra time on his hands during quarantine and decided to take a look back at speech recognition technology in the 1970s. Quickly, he started thinking to himself, “Hmm…I wonder if I could do this with an Arduino Nano?” We’ve all probably had similar thoughts, but [Peter] really put his theory to the test.
The hardware itself is pretty straightforward. There is an Arduino Nano to run the speech recognition algorithm and a MAX9814 microphone amplifier to capture the voice commands. However, the beauty of [Peter’s] approach, lies in his software implementation. [Peter] has a bit of an interplay between a custom PC program he wrote and the Arduino Nano. The learning aspect of his algorithm is done on a PC, but the implementation is done in real-time on the Arduino Nano, a typical approach for really any machine learning algorithm deployed on a microcontroller. To capture sample audio commands, or utterances, [Peter] first had to optimize the Nano’s ADC so he could get sufficient sample rates for speech processing. Doing a bit of low-level programming, he achieved a sample rate of 9ksps, which is plenty fast for audio processing.
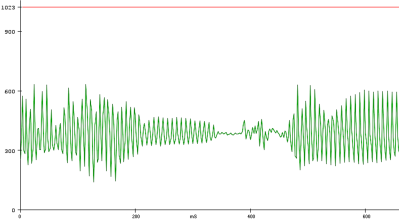
To analyze the utterances, he first divided each sample utterance into 50 ms segments. Think of dividing a single spoken word into its different syllables. Like analyzing the “se-” in “seven” separate from the “-ven.” 50 ms might be too long or too short to capture each syllable cleanly, but hopefully, that gives you a good mental picture of what [Peter’s] program is doing. He then calculated the energy of 5 different frequency bands, for every segment of every utterance. Normally that’s done using a Fourier transform, but the Nano doesn’t have enough processing power to compute the Fourier transform in real-time, so Peter tried a different approach. Instead, he implemented 5 sets of digital bandpass filters, allowing him to more easily compute the energy of the signal in each frequency band.
The energy of each frequency band for every segment is then sent to a PC where a custom-written program creates “templates” based on the sample utterances he generates. The crux of his algorithm is comparing how closely the energy of each frequency band for each utterance (and for each segment) is to the template. The PC program produces a .h file that can be compiled directly on the Nano. He uses the example of being able to recognize the numbers 0-9, but you could change those commands to “start” or “stop,” for example, if you would like to.
[Peter] admits that you can’t implement the type of speech recognition on an Arduino Nano that we’ve come to expect from those covert listening devices, but he mentions small, hands-free devices like a head-mounted multimeter could benefit from a single word or single phrase voice command. And maybe it could put your mind at ease knowing everything you say isn’t immediately getting beamed into the cloud and given to our AI overlords. Or maybe we’re all starting to get used to this. Whatever your position is on the current state of AI, hopefully, you’ve gained some inspiration for your next project.
Digital filters are always an interesting topic, and they are especially attractive with FPGAs. [Pabolo] has been working with them in a series of blog posts. The latest covers an 8th order FIR filter in Verilog. He covers some math, which you can find in many places, but he also shows how an implementation maps to DSP slices in a device. Then to reduce the number of slices, he illustrates folding which trades delay time for slice usage.
Folding takes a multi-stage parallel multiplication and breaks it into fewer multiplications done over a longer period of time. This reuses slices to reduce the number required for high-order filters.
You probably have at least a nodding familiarity with the Fourier transform, a mathematical process for transforming a time-domain signal into a frequency domain signal. In particular, for computers, we don’t really have a nice equation so we use the discrete version of the transform which takes a series of measurements at regular intervals. If you need to understand the entire frequency spectrum of a signal or you want to filter portions of the signal, this is definitely the tool for the job. However, sometimes it is more than you need.
For example, consider tuning a guitar string. You only need to know if one frequency is present or if it isn’t. If you are decoding TouchTones, you only need to know if two of eight frequencies are present. You don’t care about anything else.
A Fourier transform can do either of those jobs. But if you go that route you are going to do a lot of math to compute things you don’t care about just so you can pick out the one or two pieces you do care about. That’s the idea behind the Goertzel. It is essentially a fast Fourier transform algorithm stripped down to compute just one frequency band of interest. The math is much easier and you can usually implement it faster and smaller than a full transform, even on small CPUs.
Continue reading “DSP Spreadsheet: The Goertzel Algorithm Is Fourier’s Simpler Cousin”
