Today we heard from [Richard James Howe] about his new CPU. This new 16-bit CPU is implemented in VHDL for an FPGA.
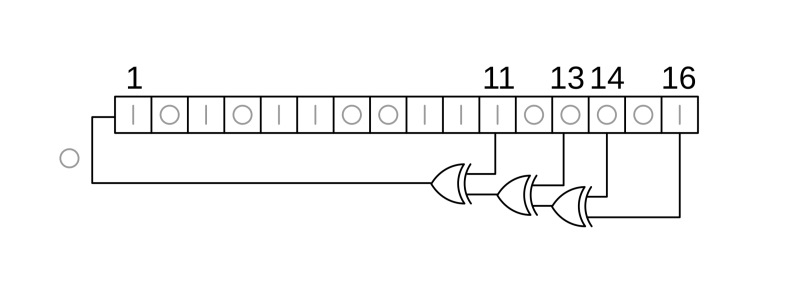
The really cool thing about this CPU is that it eschews the typical program counter (PC) and replaces it with a linear-feedback shift register (LFSR). Apparently an LFSR can be implemented in hardware with fewer transistors than are required by an adder.
Usually the program counter in your CPU increments by one, each time indicating the location of the next instruction to fetch and execute. When you replace your program counter with an LFSR it still does the same thing, indicating the next instruction to fetch and execute, but now those instructions are scattered pseudo-randomly throughout your address space!
When the instructions for your program are distributed pseudo-randomly throughout your address space you find yourself in need of a special compiler which can arrange for this to work, and that’s what this is for.
Of course all of this is shenanigans and is just for fun. This isn’t the first time we’ve heard from [Richard], we have seen his Bit-Serial CPU and Forth System-On-Chip in recent history. Glad to see he’s still at it!
Thanks to [Richard James Howe] for letting us know about this latest development.















Seems fairly straightforward. An LFSR will follow a predictable series of states in a loop, just like a counter will, and if the loop is large enough it becomes equivalent to a fairly usefully-large counter. Then you just need to develop a mapping between what would be 0,1,2,etc for the counter to the states of the LFSR. So long as this massive lookup table can fit in ram (or you can find another way to do the conversion quickly enough) then it becomes fairly straightforward to convert a program using regular ordered addresses to this new mapping where they become scattered around the address space.
I think you could have a hard time computing this lookup in reasonable time on the system using the LFSR though. Going to need a much larger computer with enough ram to hold the mapping for the entire effective address space for the LFSR computer, unless you fancy doing a lot of traversals of the LFSR’s chain of states in simulation during compile.
Couldn’t one split the counters into multiple 8-bit units that map to a single 256-byte table? Then you can run through all the values of counter zero, then counter one increments by one, etc, and OR them all together?
Except that would require a bit shift for each counter. So you could use 4 tables (1024 bytes) with the values pre-shifted, then OR them all together to map a 32-bit address.
Of course, all of these things add cycles to the calculation.
how would the upper bits know when to increment? An 8 bit lfsr has a period of 255, so you would somehow need a mechanism to only clock the upper lfsr every 255th cycle (which is even harder than the carry that normally accomplishes this in a regular PC).
Also as I alluded to, since the period of an LFSR is 2^n -1, (since the all 0 state is impossible), tying together multiple 8 bit lfsrs makes more and more invalid states where instructions cannot go. At 32 bit a full 64MB of memory would be inaccessible to the program counter (although it could potentially be used for the LD/ST subsystem)
If you have 2n storage available, you could read the ordered input sequentially and then use the LFSR to generate the write address, scattering the data across the output array. This isn’t an on-the-fly operation, but could be useful after compile/link/assemble. Would have to re-code jump addresses during processing, but that’s not hard for absolute addresses.
Not sure what you’d do about relative jumps. How do you do PC + offset, wouldn’t that put you right back at the same logic complexity as just using an ALU-based PC in the first place?
So it turns out that some LFSRs are easy to reverse. In general such reversal is a cryptographic primitive called a discrete logarithm, but there is a mathematical theory that analyzes LFSR generating polynomials, and gives ones that generate long LFSR sequences, whose values can still be inverted to give the sequence count. Look up the Pohlig algorithm.
Old Sharp 4-bit microcontrollers like one used in the Nintendo NES lock chip used a LFSR as the program counter.
It’s funny to think that this is the sort of thing that used to be important. Now days a massive increase in complexity for a tiny reduction in manufacturing costs wouldn’t make an approach like this worthwhile. It is super fun though! Since the antecedent state fully determines the next state an LFSR must start to cycle after some number of iterations which would limit the program size.
Well it would limit program size except if you used self-modifying code! And history will show that self-modifying code was a bad idea!
Any JIT compiler and any debugger is essentially a self-modifying program. Except they don’t change instructions close to the instruction pointer but in a logically separate ‘program’
So does an adding one. There are LFSR patterns that will cycle through every value except zero. It just loses a single address compared to a normal counter.
You are right of course that a program counter limits the size of a program. Of course a 64-bit program counter doesn’t limit program size in any practical sense. I hadn’t imagined that an LFSR could cycle through every value (except zero). That is kind of astonishing! Thanks for letting us know!
called maximum length LFSR, this app note has a list of taps for maximum length for 3 to 168 bits, https://docs.amd.com/v/u/en-US/xapp052
This is still relevant today for making really fast long period counters. Just not the kind that count program addresses.
LFSRs can be designed to have (2^n)-1 finite states (all zeroes is disallowed) so there isn’t much of a loss of address space.
you can alo design for all ones disallowed
Those same 4-bit Sharp microcontrollers were used in the entire Nintendo Game & Watch series spanning from 1980 to 1989. In all likelihood, it’s why Nintendo went with the Sharp SM5 series for the NES CIC in the first place.
Those same microcontrollers were heavily used in LCD handhelds from both Tiger Electronics and Konami as well. They were also cloned by Soviet manufacturer, Elektronika, for LCD handhelds made and sold in the USSR. Cloned in more ways than one, in fact, as Elektronika managed to find a way of kicking the SM5 into verification-test mode to read out the ROM, as the ROM contents for e.g. Nu, Pogodi! are known to be bit-identical to Nintendo’s “Egg” Game & Watch handheld.
The 4-bit microcontroller rabbit-hole goes much deeper than people might think, and with it, LFSR program counters.
I used a lfsr when constructing my EPROM based CPU in the 80s. It was a bad dream to compute every jmp address with paper and pencil as I have had no access to a real computer that time. Later I borrowed a TI58C programmable calculator to save some last bits of my sanity.
While using an LFSR as a program counter saves space and complicate your compiler, it may have interesting security (by obscurity) implications. Modern processors use address space randomization to make it more difficult to have a repeatable exploit, as the memory content location is offset with a random value on every boot. With the LFSR, you can randomize the LFSR’s polynomial for every instance for a similar effect, but you may want a better PRNG. Having your program randomized is going to be a pain for anyone reverse engineering the program, either way.
I cannot fully comprehend the other effects of randomizing the instruction pointer, and I wouldn’t be surprised if it somehow created novel hardware attacks. Something clever involving fault injection or side channel analysis. It’s unclear to me what the effect will be of instruction skipping if the memory space is non-linear.
if you the polynomial you’ll have to rebuild the program
You are correct. I tried to hint to it by using the word ‘instance’. E.g. every device their own unique and random layout. This is quite similar to how security devices use unique keys, and not just the same key for all the same devices.
you obviously haven’t worked in actual software development 😂
I have followed Richard’s work for some years. He has a knack for picking projects that are not exactly mainstream, and still have the opportunity for original work and innovation.
A program counter can be made from a shift register and a half adder. This adds one to the total each time – and this was frequently used on bit serial CPUs – to keep the transistor/vacuum tube count down.
Bit serial is how most computers were built – right up to the mid-1960s.
Early desktop electronic calculators also used a bit serial architecture, to keep the hardware costs down. As long as it returned an answer within half a second – that was deemed fast enough.
A bit serial ALU is used on the RCA 1802 microprocessor, which was used on the Galileo Space Probe, the first space vehicle to orbit an outer planet, Jupiter, spending almost 14 years in space.
Replacing the PC with an LSFR sounds like an interesting hobby project but I never considered that it’s actually faster and uses less transistors than a 16-bit adder. Amazing!
I see two additional downsides to this approach:
1. jump size. Often CPU architectures offer different kinds of jump instructions. A shorter and faster instruction for jumps going a short way to an instruction nearby and one that is longer and slower, but can jump farther away. The reason is usually that you can encode the shorter distance directly into an instruction while the farther jump reads the target location from a register or second instruction. Often you have tight loops or decision trees where the short jumps suffice. But this all goes away once your LFSR counter jumps all over the place.
cache. This is only relevant if your CPU has a cache, but today even small microcontrollers do. And if it is just a very small one that allows reading several instructions in parallel from a slower flash memory. Once your program counter jumps all over the place, the cache will either need to be large or refilled very often.
If you really need to reduce the number of gates used, some register lengths allow for just 2 bits, a single XOR gate, to create a max length LFSR.
Adding a single inverter can make all zeros a valid state. Either place it at the output of the XORs to invert the feedback bit, or put it on the most-significant output bit. In either case, all 1s becomes the invalid state.
When you’re using 74-TTL you have to clock some 1s into the shift register at startup. With inverted feedback, just hit the chip’s reset pin to get a valid (all 0s) starting state.
“Usually the program counter in your CPU increments by one, each time indicating the location of the next instruction to fetch and execute.
[…]
When you replace your program counter with an LFSR it still does the same thing, indicating the next instruction to fetch and execute, but now those instructions are scattered pseudo-randomly throughout your address space!”
Have there been any meetings about budget for a writer who could produce an article mentioning the advantages and drawbacks of each approach?
The advantage of the LFSR in place of the PC is that it can be implemented with fewer transistors (or you could say fewer gates). The disadvantage of the LFSR as PC is that if you use it you need to scramble your program throughout your address space. Sorry if that wasn’t clear.
Very interesting. I’ve had a similar idea for an architecture where the entire program ROM is generated by an LFSR. However because a number (an instruction) only appears once in the cycle of the LFSR, this greatly limits the possible programs. However, this can be addressed by using a much larger LFSR and then performing a modulo operation on its output, so that multiple numbers produced by the LFSR map to the same instruction.
The extraordinarily difficult piece would then be to determine the LFSR, initial conditions, and the CPU’s decode logic, to properly execute a compiled program.
Modern DRAM increases memory bandwidth by using block reads and writes. LFSR addressing makes block access impossible.
I believe there are software and hardware tricks that make relative branching possible, but the overhead for that might exceed the gains from a LFSR program counter.
I wonder would LSFR based memory access make the row hammer DRAM attack totally fail.
Another processor that uses an LFSR as a program counter is the Texas Instruments TMS1000, which was used in devices such as calculators, the Speak & Spell toy, Big Trak, Simon, and the Science Fair Microcomputer Trainer.
Way back in 1981, I was working on a speech synthesizer IC. IIRC, we were using a 500Khz crystal to run the main functions of the chip (dynamic NMOS logic and switched capacitor filters), and we used an LFSR to generate the voice pitch, since it gave us a method that used fewer gates than cascading gate trees, and also was not as much affected by gate delays.