If you ask most people to explain the Fourier series they will tell you how you can decompose any particular wave into a sum of sine waves. We’ve used that explanation before ourselves, and it is not incorrect. In fact, it is how Fourier first worked out his famous series. However, it is only part of the story and master video maker [3Blue1Brown] explains the story in his usual entertaining and informative way. You can see the video below.
Paradoxically, [3Blue1Brown] asserts that it is easier to understand the series by thinking of functions with complex number outputs producing rotating vectors in a two-dimensional space. If you watch the video, you’ll see it is an easier way to work it out and it also lets you draw very cool pictures.
Of course, our old friend the sine wave is just a special case where the imaginary part of the complex number is zero. That makes for boring drawings, but you can imagine that if you understand the complex number situation, dealing with real numbers is easy.
Another item in the video is the history of these equations. Turns out Fourier wasn’t trying to solve anything having to do with waves. He was working on the heat equation. This video is part of a series on the heat equation, but it does just fine on its own.
This topic comes up pretty regularly in part because it has so many applications from filtering to medical imaging. If you want another visualization of how little circles make waves and not just pictures, we’ve looked at that before, too.

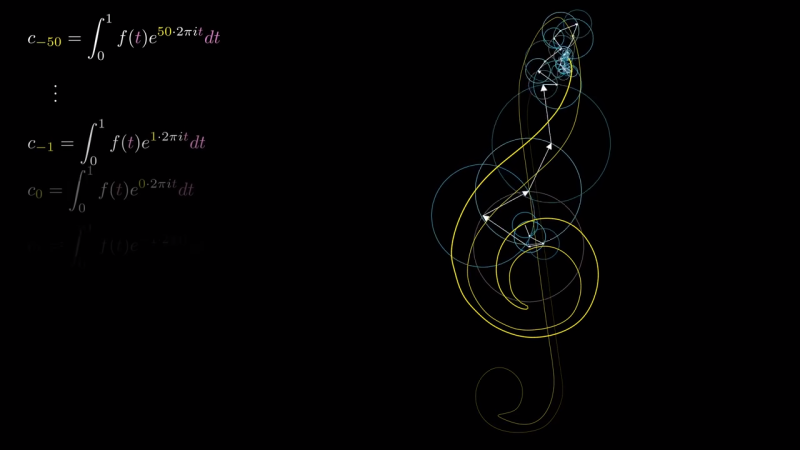














I’m fascinated with how, once you get to filtering and radio and other electronics applications, this whole thing goes from a useful abstraction to an essential truth. Like you’re used to this just being a mathematical tool but when you need explain why a square wave sounds different from a sine wave it becomes a description of reality.
Would love to see software that can generate these beautiful “circle drawings”, and how to render them. Would also love to see something like this used to create automatons or clockworks. Great video, too!
See the comments on the youtube page.
A real cool example of a fourier transform in reverse is watching harmonics from a square wave on an oscilloscope through a bandpass filter.
https://www.youtube.com/watch?v=ds0cmAV-Yek
Hmm, any ideas for a digital clock the writes the time using a Fourier series?
No idea
“If you ask most people to explain the Fourier series they will tell you how you can decompose any particular wave into a sum of sine waves”
I think you may be a little optimistic about modern society.
-most people who have an answer besides “i don’t know”
This morn, asked the first five people that walked into my office to provide “a simple and brief explanation of the fourier transform”.
Reply 1 – correct
Reply 2 – correct
Reply 3 – “transfer for whom?”
Reply 4 – correct
Reply 5 – correct
My ‘society’ seems to be good to go. Perhaps you need a more selective ‘society’.
Most people here live in a bubble too.
The basics of communication through a bandwidth which in lamen terms is a radio is even further explained down to the atom level in this video. Most people just think I am gonna push this button and I need to hear a response. But if you want to know the “why and the how this is your route.