Logic Noise is all about using analog circuits to make sounds. Preferably sound that will be enjoyable to hear and useful for making music. Now, the difference between music, sound, and noise is certainly in the ear of the behearer, but you must admit that last installment’s simple square wave lacked a little something. (Although the sync oscillator circuit extension was kinda cool.)
This week, we’ll take our single wimpy square-wave oscillator and beef it up by adding a bunch of sub-octaves to the mix. And we’ll do it using a chip that’ll be really useful for us in the future as well: the 4040 binary counter chip.
Counters (binary or decimal) are going to be fertile ground for more musical noise experiments. Why so? Because octaves are just doublings or halvings of frequencies, and because a lot of rhythmic patterns have factors of two underlying them. Just think about the most basic drum pattern you know: bass drum on the one, snare on one and three, and hi-hats on one, two, three, and four. Each different instrument fires off twice as frequently as the one before it.
But for now, enough blabber. We’ve got an oscillator to build.
Stacked Octaves Oscillator: The 4040
The 4040 (and other) binary counters do just what you’d think they do. They count up in binary. Count what? Clock pulses on the chip’s input. The 4040 is a twelve-bit binary counter, so it has twelve outputs (labelled Q in the pinout below) that display the number of pulses it’s seen on its clock input since the last chip reset. Counting up in binary turns out to be more useful than it sounds, and we’ll get to that after the chip pinout diagram.
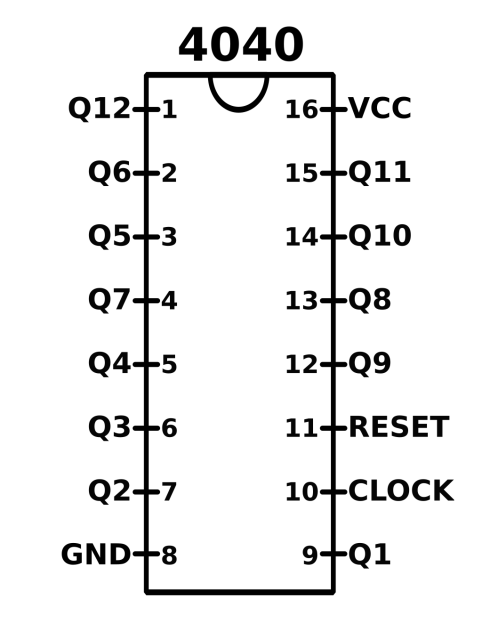
Most of the chip’s pins are taken up with these “Q” outputs. Q11 is the most-significant bit, and Q0 is the least. You could just read the number of elapsed clock cycles off of these binary outputs, but we’re going to think about this chip a little bit sideways.
Look at a counting pattern in binary: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, etc. What I’d like you to notice is that the least significant bit completes a 0-1 cycle every two counts, and that the next bit completes its 0-1 cycle every four counts, and so on. This isn’t strange. If you were to count to a million in decimal, you’d notice that the first digit completes its 0-9 cycle only after ten numbers had been counted, and that the second digit cycles ten times less frequently than the first digit and so on. We’re just not used to thinking of the frequency of change in each digit.
So if the clock input has a constant frequency, a binary counter can be used as a series of factor-of-two frequency dividers. Out of this one chip, we’ve got twelve stacked divisions of the clock input frequency, all running at once. Musically speaking, that’s twelve octaves, which is way more than the seven puny octaves you’ll find on a grand piano. In fact, the lowest octaves are likely to be periodic clicks more than anything you’d perceive as a pitch. The difference between rhythm and pitch is just a matter of degree, after all.
In fact the 4040 is built internally exactly as a cascaded series of frequency dividers, and this type of counter is called a ripple counter. The individual frequency dividers in a ripple counter are flip-flops. A flip-flop just changes state between the high and low voltages each time it gets a clock input. This is the same as dividing the frequency in half; the output requires two cycles of the input clock to get through one full high-low cycle of its own. So if you put in an 800 Hz signal, the output of a flip-flop is at 400 Hz. The 4040 is twelve of these chained together.
Before we leave the topic of counters, if you end up reading a datasheet note that some manufacturers label these outputs Q1 through Q12 instead of Q0 through Q11. Unfortunately, both options make sense. If you’re thinking of the outputs as a binary number, you’re used to thinking of the least-significant digit as the ones place, or 20. On the other hand, if you’re thinking of frequency division, the least significant output divides the input by two, or 21. I’m sticking with Q0 because it’s what my schematic editor does, but if you read along with a datasheet, you may have to convert between the two in your head.
The Circuit
So if we’ve got a source of twelve octaved square waves, let’s take some and mix them together. Simply take three high-value resistors and use them to connect three different Q outputs to your speaker’s input. I’ve used 100K resistors here, but the values aren’t critical.
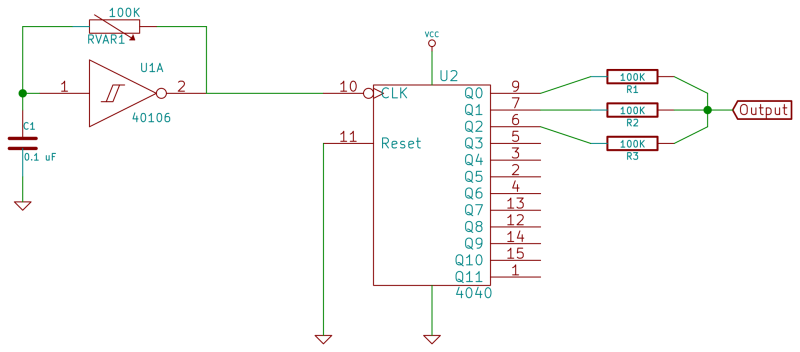
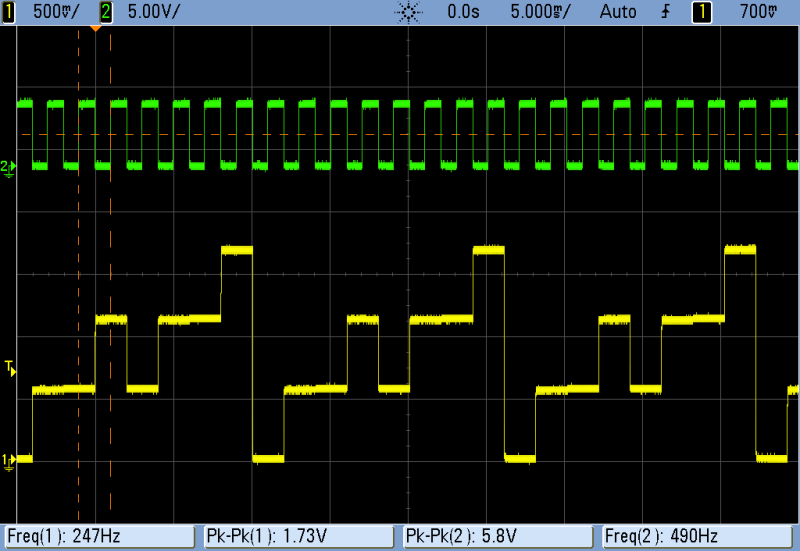
Build this up and then play around with which of the Q outputs you’re using in your mix. The three octaves just next to each other give you a classic sound. In the scope trace below, the green trace is the clock input and the yellow output is the sum of Q0, Q1, and Q2. As you can see, the result is a glitchy ramp waveform. Building up “complex” waveforms out of square waves is an old trick of the eight-bit era, so if you’re of a certain age this’ll bring back memories.
The gotchas in the circuit here include the usual caveats about providing enough local capacitance and grounding unused inputs. In this case, the unused input is the reset pin (pin 11). If you want to use it, all you need to know is that it sets all the counter outputs back to zero (low voltage) when a high voltage is present. This is handy for doing actual counting with the chip, but much less so for our purposes of pitch and rhythmic division, so we’ll just keep it grounded. But there’s probably some creative sync-oscillator setup lurking around here for you to discover and prove me wrong.
The Sync Extension
There’s no reason to feed the counter chip a simple square wave. For instance, if you just happen to have the sync oscillator sitting around on your bench from last time, try that as input to the 3-octave divider. Sometimes you one or the other output is out of the audible range, other times it’s back in. As you sweep up and down the pitch, you get ridiculous aliasing and other artifacts. We’re leaving the happy chiptunes universe and heading off somewhere else. Somewhere populated by angry machines.
Next Week
In the next installment, we’ll use the 4040 counter chip much more in line with what’s “normal” and use it to drive the eight steps of a switching sequencer using perhaps the most versatile of chips to have in your arsenal, the 4051 eight-way analog switch. So stay tuned!
















Excellent articles!
All of this has me thinking about the possibility of using delta-sigma encoding to do >1-bit synth in a digital pulse train. So, instead of operating at audio frequencies, operate at much higher frequencies, encoding the values as pulse frequencies, then turn into an analog voltage at the end with a simple lowpass filter.
Some operations are obvious: you can sum with ‘OR’ and subtract with ‘AND’ as long as the pulse trains are uncorrelated (but on the same clock). I’m pretty sure you could use a ‘voltage’ to affect a ‘frequency’ by using one output as the clock input of another generator, but then you’ve got multiple pulse trains with different – and possibly irregular – clocks, so I’m not sure how well that would work.
Thoughts?
This reminds me a lot of http://www.nicolascollins.com/handmade.htm
I had, still have, a huge amount of fun dicking about with logic ships to make audio. Looking forward to the next installment.
Acutally this all sounds pretty rad… and yes I believe that is the proper word for it!
“Logic Noise is all about using analog circuits to make sounds.”
Looks pretty digital to me.
Yeah, wait a minute! I think the original read “logic circuits” (Darn editors…)
To be fair, we’re getting close to being done with the strictly digital portion of the series. Soon we get to start torturing some of the analog out of the chips. :)
I enjoy these articles. Can’t wait to see more of them.
I like those articles. I’d like to see more of it.
This seems like an idea time to mention http://ploguechipsounds.blogspot.com/2012/09/galaxians-digital-oscillator-explained.html
Oh that’s awesome! Thank you.
When I saw the mention of a 4040, I thought to myself, “Fantastic! They’re going to be going a step forward and making a sawtooth wave rather than sticking with a square wave!” No such luck, I guess.
Wouldn’t it at least be worth mentioning that if you plumb a given amount of bits into a resistor-ladder DAC, you can use however many least-significant bits of the 4040 to generate a sawtooth wave?
Fair enough! And you totally can. I just thought that the tangled web of resistors in an R-2R DAC was enough of a hassle that I’d just keep it simple.
Riffing on that idea, what’s even more fun is to use a series of potentiometers in place of the R-2R elements. You don’t end up with anything linear, but you can make a whole bunch of different timbres with just a few bits.
Anyway, if you want sawtooths, stick around. (Short version: diode in the feedback loop of the 40106 oscillator, and tap off of the input. But first we’ll need a buffering preamp.)
I guess it’s been mentioned.
A bottle is perfect but a jar that has a top works also.
Your laboratory imported it and has sourced.