Francesco de Comité is an Associate Professor in Computer Science at the University of Sciences in Lille, France, where he researches the 2D and 3D representation of mathematical concepts and objects. He’s presented papers on a variety of topics including anamorphoses, experiments in circle packing, and Dupin cyclides. His current project involves modeling and 3D printing sea shells. He’ll be presenting a paper on the topic at Bridges Conference in July. You can find his projects on Flickr as well as on Shapeways.

Hackaday: One of your recent projects involves creating fractal patterns and warping them into biologically-correct sea shell shapes, which you then print.

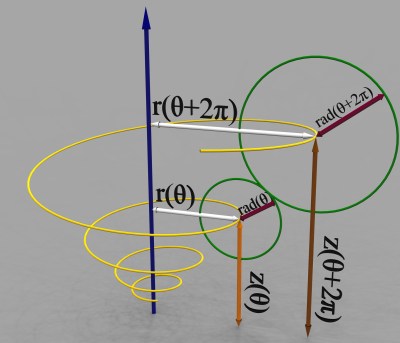
FdC: Modeling seashell shapes is an old topic–Moseley, 1838, D’Arcy Thompson beginning of 20th century. A seashell can be defined as a curve turning around an axis, while translating in the direction of this axis (i.e. on a helicoidal trajectory), and growing in size at the same time. This was modeled for computers in the ’60s by David Raup.

Drawing patterns on seashells was described by Hans Meinhardt using a model of chemical reactions (activator-inhibitor), in the same spirit as Turing’s work on morphogenesis. Combining these two works, and using 3D printers instead of 2D renderers, we can build realistic seashells, either by copying existing shells, or inventing new ones. A 3D model is not just a juxtaposition of a huge number of 2D views: manipulating 3D models can help you understand the object, find details, and so on.

I was curious to see if making a 3D seashell was possible. Moreover, I show that this can be done with simple tools — well, except the 3D printer.

Can you tell us a little about the software and hardware involved?

All the process is done using Blender, and the programs are written in Python using Blender’s script facility. The 3D printer is a ZCorp ProJet 460, which uses a powder similar to sand, and which can output colored objects.

You mentioned D’Arcy Thompson’s work at the turn of the 20th century, as well as Meinhardt more recently — was it literally a case of all of the math having been done for you already?

I have some math background, but I am more a programmer/computer scientist than a math scientist. In general, for all my works, I use maths already written by other people. Once I have coded an equation, a math concept, I can play and tune its parameters, and see what happens. We could call this ‘experimental maths’.

What was the biggest surprise or revelation you encountered while designing the shells?

3D printing is not an exact science. I made some misses, but it allows me to cut a 3D printed shell in half, and see how it was printed inside. Not exactly as I thought it would be. It gave me a better understanding of what my program was doing.

I’m reading (okay, skimming) Meinhardt’s book “The Algorithmic Beauty of Seashells” and I noticed the author included BASIC code for a seashell pattern simulator. Was that old code an example of the sort of research you had to translate into more “modern” formats?

This was a funny part of the project. In the 1990’s, the book was sold with a 3 1/2 floppy disk containing programs written in BASIC. The reader was able to generate the patterns described in the book, and test them with other parameters. Recent versions of the book don’t contain this disk anymore.

Then I found that a library in a university in Montpellier, France still had the disk. I contacted them, they found a floppy disk reader, installed it on a computer, and sent me a backup of the disk. This was the first part. I was not able to find a Basic interpreter to run the programs, so I decided to read the programs and translate them, first in Java/ImageJ to test the patterns, then in Python, to integrate them in the python script used in Blender to generate seashells.

It is disturbing to see that programs written less than 20 years ago are already difficult to use.

With regards to your work — not necessarily to nature in general — do the fractal patterns on the surface of the shell have a relationship to the curvature of the shell?

There is no link between the patterns and the shape of the shell. it looks like those are two independent processes — but I am not a biologist! In fact, you have several possibilities for putting a pattern on a shell: mapping an image on it (you consider the shell as a 2D twisted screen) This distorts the image strongly. Here is Mona Lisa (image to the right).

A lot of your projects seem to involve taking something digital and making a physical version. I can understand using a digitally controlled machine like a 3D printer, but you also do a lot of projects with cut paper, cardboard, and wire. What kind of challenges do you encounter translating your digital designs into such imperfect media?

Initially, my goal was to make mathematical concepts (curves, equations..) tangible/visible. I began with 2D images, then 3D printed objects. Trying to translate these concepts with other means came naturally. The final goal would be to build objects without using computers at all.

But I still need computers: I often create virtual versions of the objects before to build them in real world. You are right, I have to go from a perfect world to the real one. But I don’t believe this late one is imperfect; in fact the flexibility of real material is of great help, for building polyhedra with playing cards for example.

The challenge is more at the beginning of the process: how to use math to compute the right information I will need to build the object.

You’ve built a huge assortment of polyhedra out of paper. What’s the most complicated polyhedra you built that way, how did you design and build it, and how long did it take?

I am indebted to Magnus Wenninger for this part of my work. I am using his book “Polyhedron Models” in which he details models for building a lot of polyhedra; I just followed his instructions. Building a model takes 2 or 3 weeks (working in the evening only). The most complicated I tried to make was the 14th stellation of the icosahedron, but there are still a lot of models in the book I didn’t build.

One of your projects involves building digital models of Catalan solids using playing cards. What about using cards interested you as compared with (for instance) origami paper? Did you build any of the Catalan solids in real life?

The challenge is different : I generate virtual models (using Povray), varying the space between the cards, their angle, etc… When I like the model, I compute the cuts to be done in the cards, and build a template. The second part of the job is then to assemble the cards. I referred to George Hart’s work on Slide-Togethers.

The work is very different from origami. I am not able to invent origami models (just follow instructions).
Playing cards are a good material, they are at the same time rigid and flexible. Their glossy finish makes it easy to slide them one inside another.

My favorite of your projects is your Dupin cyclide series. I love how you tackle the torus using so many materials, with woven paper, cardboard, and wire versions. What about the cyclide interests you?

Cyclides can be designed using only circles. It is a non-trivial object defined by the most trivial closed curve. These circles can be cardboard disks, 3D printed rings… Working for several years now on cyclides, I have a collections of functions and programs I can manipulate like tools to model new representations.

And when I meet some problem, I can go back to the torus, solve the problem there (it is often easier), and then transform it back to compute the solution on the cyclid. I think also that cyclid are appealing for other people, they are attractive because they seem simple at first sight, then one realizes  that they are not.

Do you have any questions for [Francesco]? Leave them in comments.