If we are hiring someone such as a carpenter or an auto mechanic, we always look for two things: what kind of tools they have and what they do when things go wrong. For many types of embedded systems, one important tool that serious developers use is the Kalman filter. It is also something you use when things go “wrong.” [Carcano] recently posted a tutorial on Kalman filter equations that tries to demystify the topic. His example — a case of things going wrong — is when you have a robot that knows how far it is supposed to move and also has GPS coordinates of its positions. Since the positions probably don’t agree, you can consider that a problem with the system.
The obvious answer is to average the two positions. That’s fine if the error is small. But a Kalman filter is much more robust in more situations. [Carcano] does a good job of taking you through the math, but we will warn you it is plenty of math. If you don’t know what a Gaussian distribution is or the word covariance makes you think of sailboats, you are going to have to do some reading to get through the post.
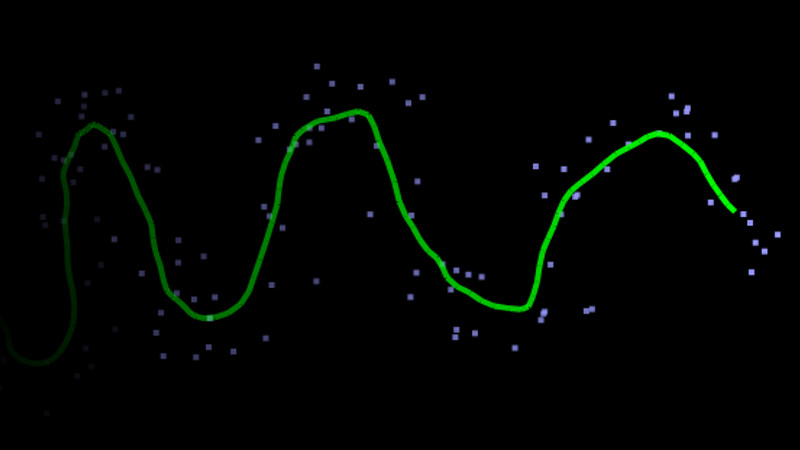
Perhaps the most fun implementation we’ve ever seen is [Richard’s] interactive Kalman filter simulation. You can set all the parameters (including random noise) and the web page will predict where your mouse cursor is as you move it. The purple dots are noisy input and the green dots are where the page thinks your mouse is. Or if you prefer videos, there is a series of seven videos from MATLAB about Kalman filters and you can see the first one, below.
This isn’t the first time we’ve looked at a walkthrough of the equations, but it has been awhile. Kalman filters show up in surprising places, like this camera autofocus mechanism.















Kalman filtering can all too easily be misapplied if not well versed in all its nuances. Two were mentioned: Gaussian and covariance. They sound “simple” but they’re not. The filter works best for linear relationships. Problem areas include encounters with non-Gaussian noise, nonlinear relationships, complicated covariance, and more. Not obvious from this simple overview is that the Kalman filter is a continuous, dynamic process (it is a filter), much more complex than a simple windowed average process (which can be very effective most of the time). There are numerous strategies to mitigate problem system dynamics. When done well, especially for simpler, ideal relationships, it can be very effective (which is why it’s used so broadly). But tread cautiously.
I agree. It is far from simple. I would also say that a big part of the problem isn’t the math, but truly understanding the system you want to control and the sources of error. Your measurements, uncertainly, and noise for example.
If anyone needs to build a Kalman Filter from scratch, you might find this helpful: https://www.amazon.com/Measurements-their-Uncertainties-practical-analysis/dp/019956633X/ref=sr_1_32?keywords=mathematics+of+uncertainty&qid=1557950488&s=gateway&sr=8-32
https://www.amazon.com/Introduction-Error-Analysis-Measurements-Uncertainties/dp/1975906659/ref=sr_1_27?keywords=mathematics+of+uncertainty&qid=1557950488&s=gateway&sr=8-27
Wanna know how I know you didn’t watch the rest of the videos in the series? :-)
Anybody who can’t handle that math is a wimp.
crap
Well. That is knowledge i just needed to finish my project. Thanks!
Kalman filters are interesting because it doesn’t seem like there’s any way to use them effectively without understanding them. They seem to be very resistant to being implemented in a black box modular library fashion, moreso than a lot of general purpose things.
In other words, you have to pre-filter your filter.
Not at all, its all in the math And of course dependent upon the application :-)
This is a very useful filtering technique, got most of my education in this after uni enginnering from a visiting Indian engineer (Indisa Rajasingham) circa 1979 when working on Mt Newman minings nucleonic ore flow gauge setup ie pair of collimated beta beams 1m vertical separation detecting change in count rate due from iron ore. Ostensibly acceleration due to gravity shifted the count rate indicative of mass flow. Kalman filter approach fixed delay and noise issues very well indeed, Arj Indi is on facebook. More info I wrote here on this 2 years back https://hackaday.com/2017/05/01/a-brief-history-of-radioactivity/
These days can apply Kalman filters to very odd problems or metrics of detection in psychology within, mass marketing and of course stocks and shares too in respect of probabilistic positioning as well as the more mundane engineering problems pretty well fixed in last 3 decades ;-)
Thanks for post, provokes me to review recent trends in applying Kalman to robotic controls.