The simple definition of a mean is that of a numeric quantity which represents the center of a collection of numbers. Here the trick lies in defining the exact type of numeric collection, as beyond the arithmetic mean (AM for short, the sum of all values divided by their number) there are many more, with the other two classical Pythagorean means being the geometric mean (GM) and harmonic mean (HM).
The question that many start off with, is what the GM and AM are and why you’d want to use them, which is why [W.D.] wrote a blog post on that topic that they figure should be somewhat intuitive relative to digging through search results, or consulting the Wikipedia entries.
Compared to the AM, the GM uses the product of the values rather than the sum, which makes it a good fit for e.g. changes in a percentage data set. One thing that [W.D] argues for is to use logarithms to grasp the GM, as this makes it more obvious and closer to taking the AM. Finally, the HM is useful for something like the average speed across multiple trips, and is perhaps the easiest to grasp.
Ultimately, the Pythagorean means and their non-Pythagorean brethren are useful for things like data analysis and statistics, where using the right mean can reveal interesting data, much like how other types using something like the median can make a lot more sense. The latter obviously mostly in the hazy field of statistics.
No matter what approach works for you to make these concepts ‘click’, they’re all very useful things to comprehend, as much of every day life revolves around them, including concepts like ‘mean time to failure’ for parts.
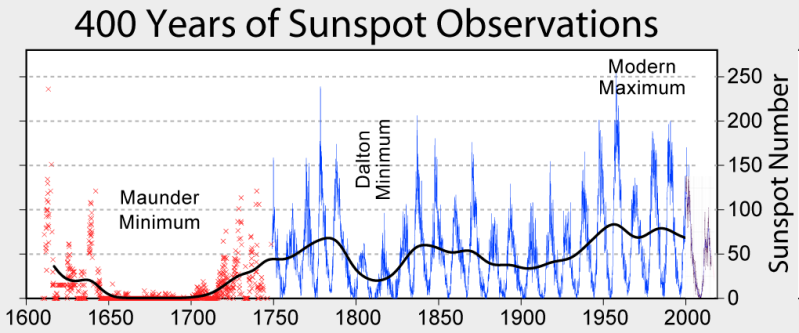
Top image: Cycles of sunspots for the last 400 years as an example data set to apply statistical interpretations to. (Credit: Robert A. Rohde, CC BY-SA 3.0)















The total resistance of a set of resistors in parallel is the harmonic mean. I’m surprised Maya didn’t mention this, given that it’s Hackaday.
Additionally, we recently had an article asking about using technology to help learning. Suppose we write down a set of concepts or ideas that make up cultural literacy. In other words, we have a list of words that we believe everyone should know in order to survive in the modern world – concepts needed to fill out an employment form, understand a political speech, read a news article, and so on.
Once we have that list, for each item we can add references to some really good introductions and explanations of that concept, then create a curriculum that goes through the concepts sorted by fundamental order, so that kids could go through the curriculum at their own pace.
For example, one concept might be “star chamber”, an idiom that is sometimes encountered and referenced in written text. The universal curriculum could point to a definition of the word, but also note the movie “star chamber” (starring Michael Douglas) that goes through not only the concept, but some of the philosophical ramifications. A kid could sit down, watch that movie, and get a deep understanding of the concept.
Wikipedia and other encyclopedias are basically “all concepts”, but aren’t really structured for learning, nor is there any sense of which Wikipedia concepts are common and which are rare.
The book “Cultural Literacy” (E. D. Hirsch) attempts to make such a list. The back appendix is a list of words and phrases that everyone is expected to know. I chose “star chamber” at random from that list.
I’d never heard of “geometric mean” until today, and I’ve known how to calculate parallel resistances since I was a young pup.
thanks! i knew there had to be a good one-sentence description of harmonic mean that was inexplicably omitted from the article…and here it’s the first sentence of the first comment.
If you take an EE course, sometimes the professor will use || as an operator in the algebraic equations, things like “R1 || R2” as shorthand for the harmonic mean operator.
This got me thinking about numeric operators in languages, and why we only have the basic four. Perl has a plethora of operators, but it doesn’t have this one.
Perhaps the arithmetic mean (of 2 numbers) should also be an operator.
Like the insight this article brings, the unification :)
For funsies:
R(3) + (R(20) || R(10) || R(20))in C++ on Compiler Explorer:https://godbolt.org/z/f9fbn1q3P
When you tell a girl she is average, and she replies “you too”, that’s harmonic mean.
parallel resistors are harmonic mean over n I think. E.g. harmonic mean of (100, 10) = 18.2, but (100 || 10) = 9.1; i.e. 18.2 / 2
But thanks anyway; I never thought about that in terms of harmonic mean.
And thanks to the article for the article for the ‘grand unification of means’ via functional transforms mapping them all to arithmetic means.
It just goes to show that Hackaday comments are increasingly mean.
B^)
Average, really