Function Generator With Zero CPU Cycles

October 22, 2014 by Brian Benchoff 34 Comments

No one is sitting around their workbench trying to come up with the next great oscilloscope or multimeter, but function generators still remain one of the pieces of test equipment anyone – even someone with an Arduino starter pack – can build at home. Most of these function generators aren’t very good; you’re lucky if you can get a sine wave above the audio spectrum. [Bruce Land] had the idea to play around with DMA channels on a PIC32 and ended up with a function generator that uses zero CPU cycles. It’s perfect for a homebrew function generator build, or even a very cool audio synthesizer.

The main obstacles to generating a good sine wave at high frequencies are a high sample rate and an accurate DAC. For homebrew function generators, it’s usually the sample rate that’s terrible; it’s hard pushing bits out a port that fast. By using the DMA channel on a PIC32, [Bruce] can shove arbitrary waveforms out of the chip without using any CPU cycles. By writing a sine wave, or any other wave for that matter, to memory, the PIC32 will just spit them out and leave the CPU to do more important work.

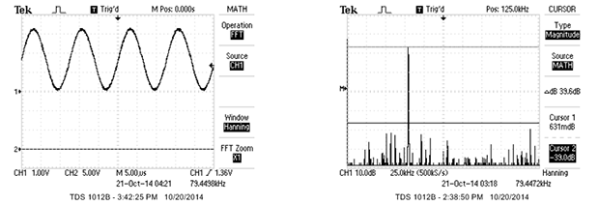
[Bruce] was able to generate a great-looking sine wave up to 200 kHz, and the highest amplitude of the harmonics was about 40db below the fundamental up to 100 kHz. That’s a spectacular sine wave, and the perfect basis for a DIY function generator build.

Sine Waves, Squares Waves, And The Occasional FFT

October 1, 2014 by Bil Herd 35 Comments

I became aware of harmonics and the sound of different shaped waveforms early in my electronics career (mid 1970’s) as I was an avid fan of [Emerson Lake and Palmer], [Pink Floyd], [Yes], and the list goes on. I knew every note of [Karn Evil 9] and could hear the sweeping filters and the fundamental wave shapes underneath it.

I remember coming to the understanding that a square wave, which is a collection of fundamental and (odd) harmonics frequencies, could then be used to give an indication of frequency response. If the high frequencies were missing the sharp edges of the square wave would round off. The opposite was then true, if the low frequencies were missing the square wave couldn’t “hold” its value and the top plateau would start to sag.

Continue reading “Sine Waves, Squares Waves, And The Occasional FFT” →