Linear transforms — like a Fourier transform — are a key math tool in engineering and science. A team from UCLA recently published a paper describing how they used deep learning techniques to design an all-optical solution for arbitrary linear transforms. The technique doesn’t use any conventional processing elements and, instead, relies on diffractive surfaces. They also describe a “data free” design approach that does not rely on deep learning.
There is obvious appeal to using light to compute transforms. The computation occurs at the speed of light and in a highly parallel fashion. The final system will have multiple diffractive surfaces to compute the final result.
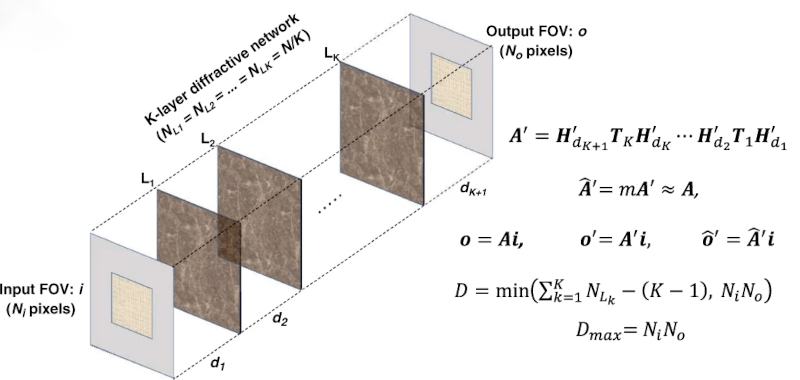
The deep learning the paper’s authors refer to was all set up with TensorFlow using the Adam optimizer. It appears that the paper relies on simulations of the diffraction surfaces, not an actual implementation. We aren’t sure how hard it is to realize high-resolution diffraction surfaces with the very specific patterns called for by the designs.
If you are looking to get started with TensorFlow yourself, we’ve covered quite a few tutorials. On the other hand, we talk quite a bit about Fourier transforms, too.















I could see this being a feature of space-craft with low power requirements. It could also become a part of M/A/V/R headsets.
Nice to see that optical Fourier is finally making a comeback. We used it in the 80s for feature detection in manufacturing inspection systems.
I used this technique for my final engineering school project with a red laser and aerial photos, trying to find some Roman centuriations (cadastre) : parcels are squares roughly 710 m on a side … It was a long time ago (1974 !)
Optalysys in the UK have been doing this for years. First using spatial light modulators and moved on to faster silicon photonics. https://optalysys.com/
What about an optical Bitcoin miner? Free Money?
I don’t think that could be made to work. Fourier transforms are essentially an analogue (continuous) process. Calculating hashes is very much digital (discrete).
Perhaps not applicable to the case of crypto-hashes, but the Discrete Fourier transform is discrete including aperiodic signals. Then there is the seemingly discrete nature of sorting, which, it turns out, can be done in a continuous manner: http://hrl.harvard.edu/analog/
Reminds me of my PhD project where I used a transmissive LCD as the input to such a system making it possible to process images in real time. At the Fourier plane you could filter images by blocking / passing unwanted frequencies etc.
I am pretty sure Applied Science mentioned somewhat similar in some of his YouTube movie.
*ALL* synthetic aperture radar data was processed by optical transforms when SAR technology was developed in the 1960’s.
With the resolution developed for IC production, custom operators are unlikely to be difficult. Merely expensive if you need to make a change.
Basically a Chinese journal published with the name Nature is ready to accept any garbage you throw at it.
This is introductory optics.
Yes, people have used the Fourier transforming properties of light since before the laser, in particular for optical correlators.
I’m disappointed in Hack a Day for promoting this dude’s work.
Well, while diffraction-based linear transforms aren’t crazy new, I think the deep learning method of determining what those diffraction surfaces look like is novel and interesting.
That’s fair, but the light/optical transform aspect of the title certainly caught my attention as something we’ve been doing at least since Newton.
Anyhow, always enjoy your articles Al.
Nature is a top publication for a lot of fields.
We did OCR with this technique in college in the early 90s.i remember it as one of the most exciting physics experiments I got to do.
This was touched on by Huygens Optics in https://www.youtube.com/watch?v=Y9FZ4igNxNA.